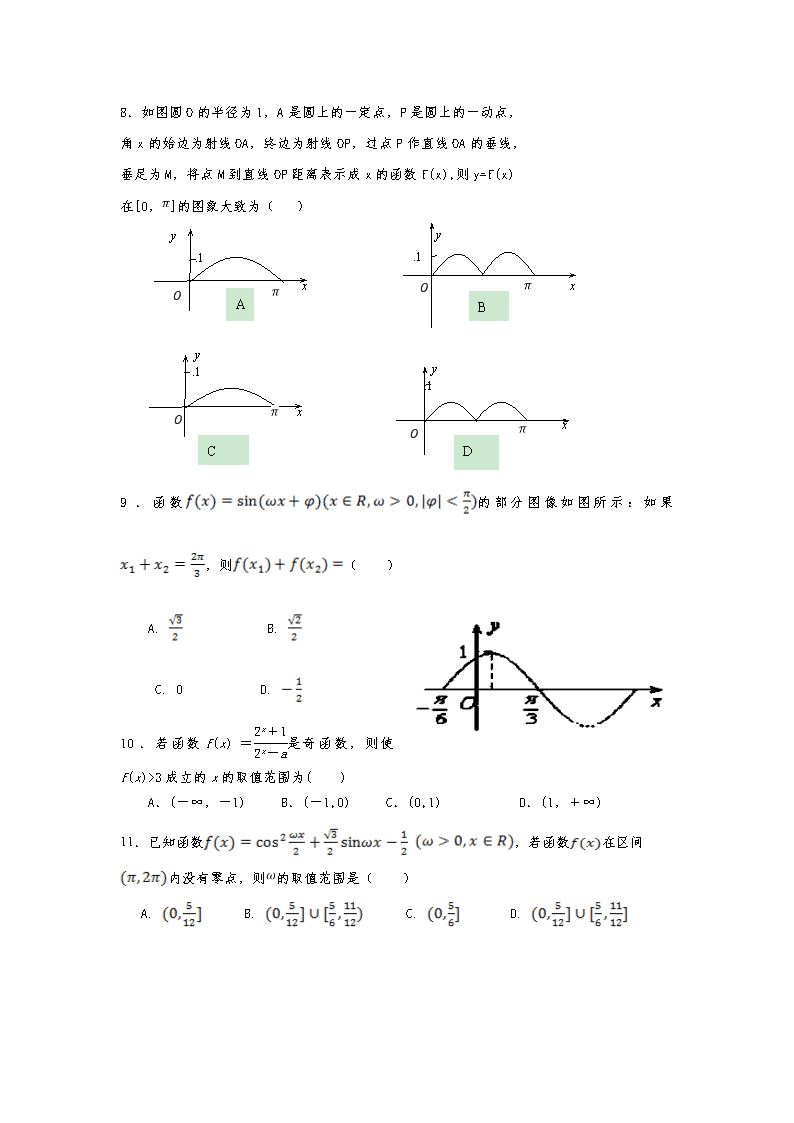- 440.00 KB
- 2021-04-14 发布
平遥和诚学校2017-2018学年高三11月月考
数学试卷(文科)
考试时间:120分钟 满分:150分 命题人
一、选择题(本小题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.集合A={y|y=,0≤x≤4},B={x|x2-x>0},则A∩B=( )
A.(-∞,1]∪(2,+∞) B.(-∞,0)∪(1,2) C. D.(1,2]
2.已知ω>0,函数f(x)=sin在上单调递减,则ω的取值范围是( )
A. B. C. D.(0,2]
3.已知cosα=,cos(α+β)=-,且α,β∈,则cos(α-β)=( )
A.- B. C.- D.
4.将函数(,)图象上所有点的横坐标缩短为原来的一半,再向右平移个单位长度得到函数的图象,则,的值分别为( )
A., B. C. D.
5.在ABC中,点D在线段BC的延长线上,且BC=3CD,点O在线段CD上(与点C、D不重合),若,则x的取值范围是( )
A.(0,) B.(0,) C.(- ) D.(- )
6.已知x,y满足且z=2x+y的最大值是最小值的4倍,则a的值是( )
A. B. C. D.4
7.定义在R上的函数f(x)满足f(-x)=-f(x),f (x-2)=f(x+2),且x∈(-1,0)时,f(x)=2x+,则f(log220)等于( )
x
O
P
M
A
A.1 B. C.-1 D.-
8.如图圆O的半径为1,A是圆上的一定点,P是圆上的一动点,
角x的始边为射线OA,终边为射线OP,过点P作直线OA的垂线,
垂足为M,将点M到直线OP距离表示成x的函数f(x),则y=f(x)
在[0,]的图象大致为( )
x
.1
y
O
O
.1
y
B
x
A
x
.1
y
O
C
O
.1
y
D
x
9.函数的部分图像如图所示:如果,则( )
A. B.
C. 0 D.
10.若函数f(x)=是奇函数,则使f(x)>3成立的x的取值范围为( )
A.(-∞,-1) B.(-1,0) C.(0,1) D.(1,+∞)
11.已知函数 ,若函数在区间内没有零点,则的取值范围是( )
A. B. C. D.
12.函数的图象与直线从左至右分别交于点,与直线从左至右分别交于点.记线段和在轴上的投影长度分别为,则的最小值为( )
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,共20分)
13.已知向量a,b的夹角450,且|a|=1,|2a-b|=,则|b|=
14.已知a>0,b>0,ab=8,则当a的值为________时,log2a·log2(2b)取得最大值.
15.设当x= 时,f(x)=sinx-2cosx取得最大值,则cos=
16.定义在上的单调函数,,,则方程
的解所在的区间是
三.解答题(17-21为必做题,共5个小题,每小题12分;22-23为必选作题,从中选作1题10分;共70分)
【17-21为必做题】
17(12分).已知函数f()= ,.
(1) 求f()的最小正周期;
(2) 求f()在区间[- ,]的最大值和最小值。
18(12分).在△ABC中,角A,B,C的对边分别为a,b,c,且
2cos2cosB-sin(A-B)sinB-cosB=-.
(1)求cosA的值;
(2)若a=4,b=5,求B和c.
19(12分).已知函数f(x)=2asinωxcosωx+2cos2ωx-(a>0,ω>0)的最大值为2,且最小正周期为π.
(1)求函数f(x)的解析式及其对称轴方程;
(2)若f(α)=,求sin的值.
20(12分).为了净化空气,某科研单位根据实验得出,在一定范围内,每喷洒1个单位的净化剂,空气中释放的净化剂浓度y(单位:毫克/立方米)随着时间x(单位:天)变化的函数关系式近似为y=
若多次喷洒,则某一时刻空气中的净化剂浓度为每次喷洒的净化剂在相应时刻所释放的浓度之和.由实验知,当空气中净化剂的浓度不低于4(毫克/立方米)时,它才能起到净化空气的作用.
(1)若一次喷洒4个单位的净化剂,则净化时间可达几天?
(2)若第一次喷洒2个单位的净化剂,6天后再喷洒a(1≤a≤4)个单位的净化剂,要使接下来的4天中能够持续有效净化,试求a的最小值(精确到0.1,参考数据:取1.4).
21(12分).已知函数.
(1)当时,求函数的最小值;
(2)若在上单调递增,求实数的取值范围.
【22-23为选作题,从中选作1题】
22(10分).在直角坐标系xOy中,直线C1:x=-2,圆C2:(x-1)2+(y-2)2=1,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系.
(1)求C1,C2的极坐标方程;
(2)若直线C3的极坐标方程为θ=(ρ∈R),设C2与C3的交点为M,N,求△C2MN 的面积.
23(10分).设函数f(x)=|2x+1|-|x-4|.
(1)解不等式f(x)>2;
(2)若关于x的不等式a>f(x)有解,求实数a的取值范围.
和诚学校2017-2018学年高三11月月考
数学答案(文科)
一、1.D 2.A. 3.D.4.A 5.C 6. B 7.C, 8.C 9.C. 10.C 11.D 12.B
二、13.3 14.4 15.- 16.
三.
17答案:(1)f()= sin(2x-),T==
(2)最大值为,最小值为-
18解 (1)由2cos2cosB-sin(A-B)sinB-cosB=-,得
[cos(A-B)+1]cosB-sin(A-B)sinB-cosB=-.
即cos(A-B)cosB-sin(A-B)sinB=-,则cos(A-B+B)=-.
因此,cosA=-.
(2)由cosA=-,0<A<π,得sinA=,
由正弦定理,有=,a=4,b=5,
所以sinB==.
由题知a>b,则A>B,故B=.
根据余弦定理有(4)2=52+c2-2×5c×,
整理得c2+6c-7=0,
解得c=1或c=-7(舍去).
19解(1)f(x)=asin2ωx+cos2ωx=sin(2ωx+φ),
由题意知:f(x)的最小正周期为π,由=π,知ω=1,
由f(x)最大值为2,故=2,又a>0,
∴a=1,tan φ=.
∴f(x)=2sin,
令2x+=kπ+,得x=+(k∈Z).
故f(x)的对称轴方程为x=+(k∈Z).
(2)由f(α)=知2sin=,即sin=,
∴sin=sin=-cos2
=-1+2sin2=-1+2×=-.
20解:(1)因为一次喷洒4个单位的净化剂,
所以浓度f(x)=4y=
则当0≤x≤4时,由-4≥4解得0≤x<8,所以此时0≤x≤4.
当44.
所以不等式的解集为.
(2)f(x)=
可知在上,f(x)单调递减;在 上,f(x)单调递增.
要a>f(x)有解,只要a>f(x)min.
由f(x)单调性知f(x)min=f=-.
所以实数a的取值范围是.