湖北省仙桃市沔州中学高三物理期中考试卷 人教版 11页

湖北省仙桃市沔州中学高三物理期中考试卷 ‎ 二、选择题（每小题包括8小题。每小题给出的四个选项中，有的只有一个选项正确，有的有多个选项正确，全部选对的得6分，选对但不全的得3分，有选错的得0分）‎ k2‎ k1‎ P Q m ‎14．如图所示，两个弹簧的质量不计，劲度系数分别为k1、k2，它们的一端固定在质量为m的物体上，另一端分别固定在P、Q点，当物体平衡时，上面的弹簧k2处于原长，若要把物体的质量换成‎2 m（物体的大小不变，且两弹簧均在的弹性限度内），再次平衡时，物体比第一次平衡时下降的距离x为（ ）‎ ‎（A）mg／(k1+k2) （B）k1k‎2 m g / (k1+k2)‎ ‎（C）‎2 m g / (k1+k2) （D）2 k1 k‎2 m g / (k1+k2)‎ ‎15．两个倾角相同的滑杆上分别套A、B两圆环，两环上分别用细线悬吊着两物体C、D，如图所示，当它们都沿滑杆向下滑动时，A的悬线与杆垂直，B的悬线竖直向下。则( )‎ θ θ A．A环与杆无摩擦力 B．B环与杆无摩擦力 C．A环做的是匀速运动 D．B环做的是匀速运动 ‎16．如图所示，质量均为m的A、B两球穿在水平杆CD上，两球与杆的最大静磨擦力均为fm，OO/为杆CD的转轴，A、B两球之间有一根长为3R的轻绳连接，两球到转轴的距离AO＝R，BO＝2R，若使杆CD绕OO’轴转动时A、B两球能保持和杆相对静止，则杆CD转动时角速度的最大值是（ ）‎ ‎（A），（B），（C），（D）。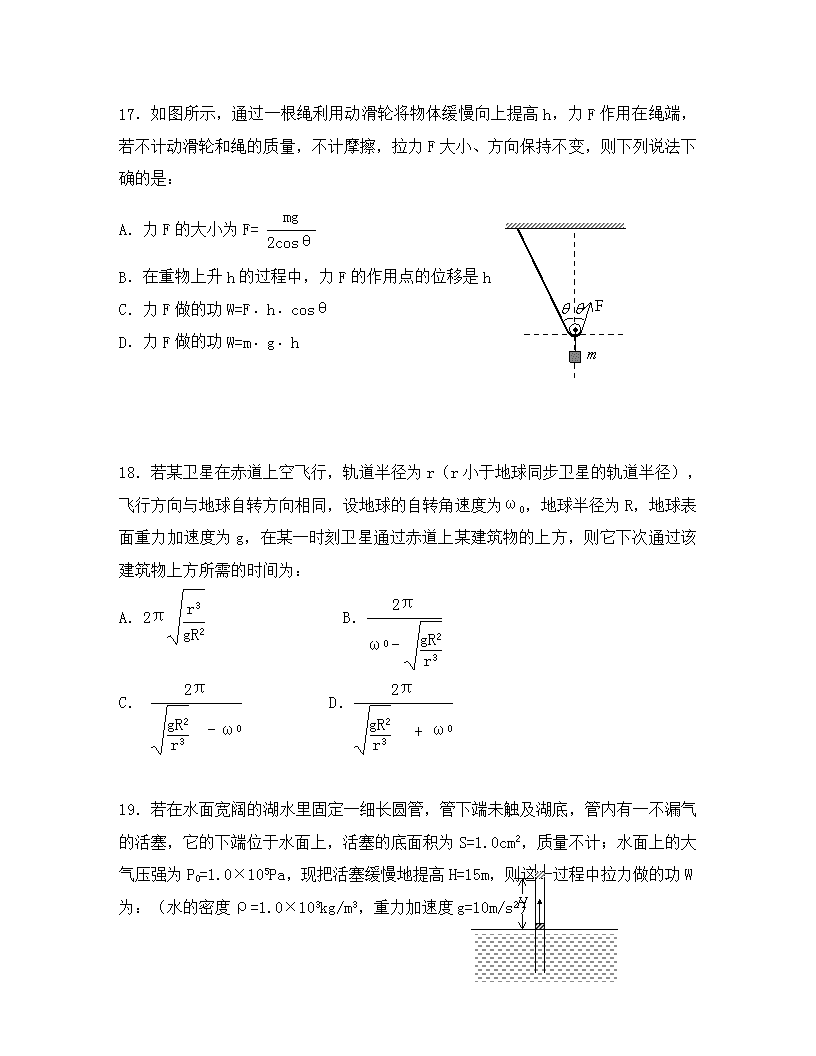 ‎ ‎17．如图所示，通过一根绳利用动滑轮将物体缓慢向上提高h，力F作用在绳端，若不计动滑轮和绳的质量，不计摩擦，拉力F大小、方向保持不变，则下列说法下确的是：‎ A．力F的大小为F= B．在重物上升h的过程中，力F的作用点的位移是h C．力F做的功W=F﹒h﹒cosθ D．力F做的功W=m﹒g﹒h ‎18．若某卫星在赤道上空飞行，轨道半径为r（r小于地球同步卫星的轨道半径），飞行方向与地球自转方向相同，设地球的自转角速度为ω0，地球半径为R，地球表面重力加速度为g，在某一时刻卫星通过赤道上某建筑物的上方，则它下次通过该建筑物上方所需的时间为：‎ A．2π B． C． D． ‎19．若在水面宽阔的湖水里固定一细长圆管，管下端未触及湖底，管内有一不漏气的活塞，它的下端位于水面上，活塞的底面积为S=‎1.0cm2，质量不计；水面上的大气压强为P0=1.0×105Pa，现把活塞缓慢地提高H=‎15m，则这一过程中拉力做的功W为：（水的密度ρ=1.0×‎103kg/m3，重力加速度g=‎10m/s2）‎ A．50J B．75J C．100J D．150J B A h ‎20．如图所示，一物体由A点以初速度v0下滑到底端B，它与挡板B做无动能损失的碰撞后又滑回到A点，其速度正好为零，设A、B两点间高度为h，则它与挡板碰撞前的速度大小为：‎ A． B． C． D． ‎21.如图所示，水平放置的两根足够长的平行光滑杆AB和CD，各穿有质量为M和m的小球（可视为质点），两杆之间相距为a，两球用原长也为a的轻弹簧连接，现在把M球从左边用挡板挡住，用力将m向左拉一段距离，则释放m后：‎ a M m A B C D A．在弹簧第一次恢复原长的过程中，两球和弹簧组成的系统动量守恒，机械能也守恒。‎ B．在弹簧第二次恢复原长时，M的速度达最大。‎ C．在弹簧第一次恢复原长以后继续运动过程中，两球和弹簧组成的系统动量不守恒、机械能守恒。‎ D．在弹簧第一次恢复原长以后继续运动过程中，两球和弹簧组成的系统动量守恒、机械能也守恒。‎ 实验题：‎ ‎22．（16分）（1）如图所示，是用自由落体法验证机械能守恒定律时得到的一条纸带，我们选中N点来验证机械能守恒定律，下列有关说法正确的是：‎ A．N点的速度vn可用vn=g﹒n﹒T来计算（T=0.02s，g为当地的重力加速度值）。‎ B．N点的速度vn可用vn= 来计算。‎ C．N点的速度vn用vn= 或vn=g﹒n﹒T计算均可以（T=0.02s，g为当地的重力加速度值）。‎ D．验证机械能守恒，就是看mvn2 是否等于mghn(m为重锤的质量，需用天平称量；g为当地的重力加速度值)‎ ‎（2）如图为一小球做平抛运动的闪光照片的一部分，图中背景方格的边长均为‎5cm，如果取g=‎10m/s2，那么①闪光的频率是 ，②小球运动中水平分速度的大小是 m/s。③小球经过B点时，小球平抛运动的时间是 s。‎ ‎（3）用如图所示装置做验证动量守恒定律实验，不需要测定的物理量是：（ ）‎ A．入射小球和被碰小球的质量m1、m2‎ B．半径相同的入射小球和被碰小球的直径 C．斜槽轨道的末端距地面的高度 D．入射小球未碰撞时飞出的水平距离 E．入射小球开始滚下时的初始位置与碰撞前位置的高度差。‎ ‎23.（16分）一个同学身高h1=‎1.8m，质量m=‎60kg，站立举手摸高（指手能摸到的最大高度）h2=‎2.2m．该同学先身体下蹲，重心比站立时下降∆h=‎0.4m，然后用力蹬地竖直离地跳起，‎ 摸高为h3=‎3.0m．假定他蹬地的过程中，地面对他的力F为恒力，重力加速度g=‎10m/s2求:‎ ‎(1) 地面对他的力F的大小．‎ ‎(2) 地面对他的力F的功W ‎(3) 地面对他的力F的冲量 I ‎24．（20分）如图所示，A和B并排放在光滑的水平面上，A上开有一光滑的、半径为R的半圆轨道，半圆轨道右侧顶点有一小物体C，C由顶点自由滑下，设A、B、C的质量均为m，求：‎ ‎（1）A、B分离时B的速度多大？‎ ‎（2）C由顶点滑下到轨道最点后，沿轨道上升的最大高度是多少？‎ ‎25．（20分）如图所示，右端有固定挡板的滑块B放在光滑的水平面上，B的质量M=‎0.8kg，右端离墙的距离L=‎0.09m，在B上靠近挡板处放一质量m=‎0.2kg的小金属块A。A和挡板之间有少量炸药。A和B之间的动摩擦因数μ=0.2。点燃炸药，瞬间释放化学能。设有E0=0.5J的能量转化为A和B的动能。当B向右运动与墙壁发生碰撞后，立即以碰撞前的速率向左运动，A始终末滑离B。g=‎10m/s2，求：‎ ‎（1）A和B刚开始运动时的速度vA、vB ‎（2）最终A在B上相对滑行的距离S ‎[参考答案]‎ ‎14．A 15．AD 16．B 17．AD 18．C 19．C 20．C 21．BD ‎ ‎22． (1)B ‎ ‎(2)①10 ② 1.5 ③ 0.2 ‎ ‎(3) BCE ‎23. 解：（1）设人在蹬在竖直上升过程中的加速度为a1,身体伸直离地时的速度为v 由牛顿第二定律得：‎ F－mg=ma1‎ 由运动学公式，人在上升过程有：‎ v2=‎2 a1﹒∆h 由运动学公式，人在离地后竖直上抛运动有：‎ v2=‎2 g(h3－h2)‎ 代数据得：a1=‎20 m/s‎2 F=1800N ‎（2）地面对人的力F位移为零，不做功，故W=0‎ ‎（3）人蹬地的时间为t 由运动学公式：∆h=a1t2‎ 代数据得：t=0.2s 力F的冲量 I=F﹒t=1800×0.2=360N·S ‎24. （1）设C下滑至轨道最低点时，C的速度为vC，此时A、B分离，分离时A、B的速度相等，即：vA=vB 对A、B、C组成的物体系，根据机械能守恒定律：‎ mgR=++‎ 此时A、B、C组成的物体系，水平方向上动量守恒，取水平向右为正方向，有 ‎–mvC+mvA+mvB=0‎ 解方程①②③得：vA=vB= vc=2 ‎(2) C滑至最大高度时，A、C的速度相同，设它们 的共同速度为v共，因A、C组成的系统水平方向动量仍守恒，所以：‎ m vc－m·vA=‎2m v共 ‎ A、C组成的系统，在上升过程中，由机械能守恒定律有：‎ ‎+= mgh+‎ 解得：h= ‎25．解：（1）A和B在炸药点燃前后动量守恒，设向左为正 mvA–MvB=0‎ mvA2+MvB2=E0‎ 解得：v A=‎2m/s 方向向左 v B=‎0.5m/s 方向向右 ‎（2）B运动到墙壁处时，设A和B的速度分别是vA/、vB/对A和B构成的系统，由动量守恒定律，设向左为正 mvA–MvB=mvA/–MvB/‎ 对B由动能定理：–μmgL=－‎ 解得：vA/=‎1.6m/s vB/=‎0.4m/s 设A、B最终保持相对静止时的共同速度为v 由动量守恒定律：mvA/+ MvB/=(M+m)v 由能的转化和守恒定律：E0=μmgS+(M+m)v2‎ 解得：S=‎‎0.74m k