- 871.00 KB
- 2021-04-14 发布
长安一中2017~2018学年度第一学期期末考试
高二数学试题(文科)
命题人:贺永安审题人:罗理想
一、选择题(本大题共14小题,每小题5分,共70分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.命题“若,则”的否命题是( )
A.若,则 B.若,则
C.若,则 D.若,则.
2.某学校为了了解三年级、六年级、九年级这三个年级之间的学生视力是否存在显著差异,拟从这三个年级中按人数比例抽取部分学生进行调查,则最合理的抽样方法是( )
A.抽签法 B.系统抽样法C.分层抽样法D. 随机数法
3.双曲线的顶点到其渐近线的距离等于()
A.2 B.1 C. D.
4.设,若,则等于( )
A. B. C. D.
5.为评估一种农作物的种植效果,选了块地作试验田.这块地的亩产量(单位:)分别为,下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是( )
A.的平均数 B.的标准差
C.的最大值 D.的中位数
6.如图所示的茎叶图记录了甲、乙两组各5名工人某日的产量数据(单位:件).若这两组数据的中位数相等,且平均值也相等,则和的值分别为( )
A. 3,5 B. 5,5 C. 3,7 D. 5,7
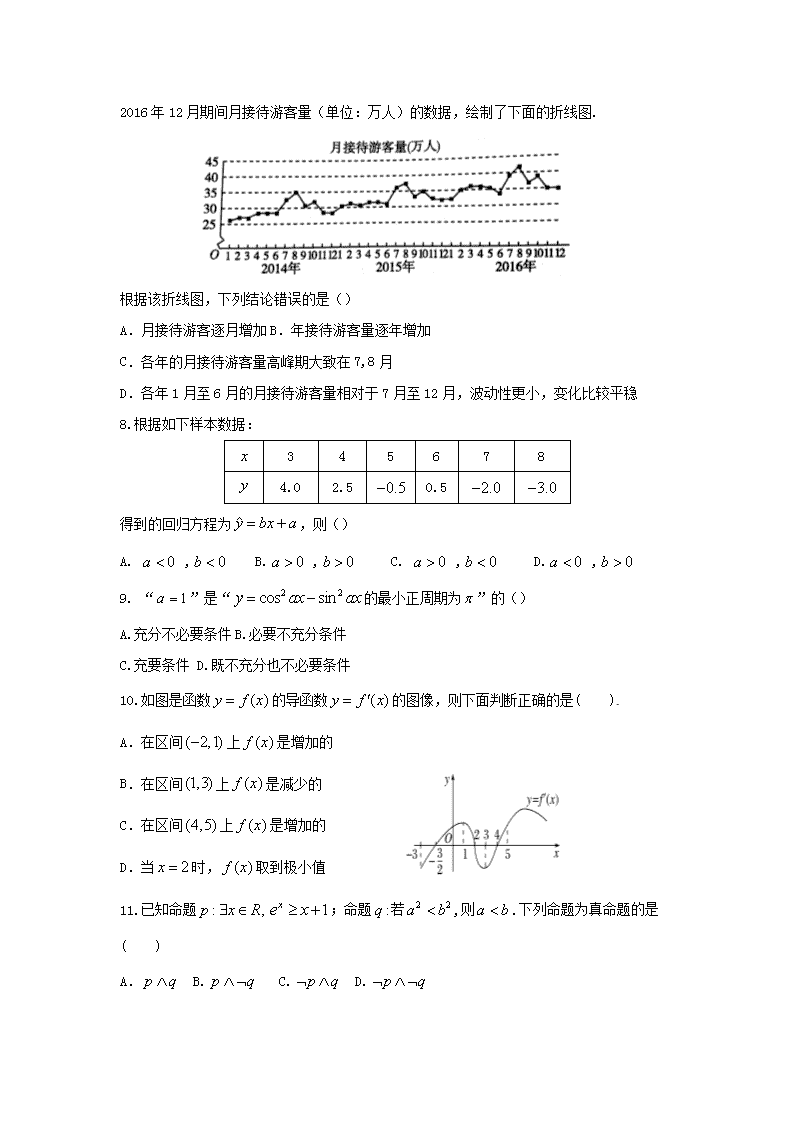
7.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至
2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.
根据该折线图,下列结论错误的是()
A.月接待游客逐月增加B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
8.根据如下样本数据:
3
4
5
6
7
8
4.0
2.5
0.5
得到的回归方程为,则()
A. , B. , C. , D. ,
9. “”是“的最小正周期为”的()
A.充分不必要条件B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
10.如图是函数的导函数的图像,则下面判断正确的是( )
A.在区间上是增加的
B.在区间上是减少的
C.在区间上是增加的
D.当时,取到极小值
11.已知命题;命题若,则.下列命题为真命题的是( )
A. B. C. D.
12.已知双曲线的左焦点为,点在双曲线的渐近线上,是边长为2的等边三角形(为原点),则双曲线的方程为()
A. B.C.D.
13.现采用随机模拟的方法估计某运动员射击4次,至少击中3次的概率:先由计算机给出0到9之间取整数值的随机数,指定0,1表示没有击中目标,2,3,4,5,6,7,8,9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20组随机数:
7527 0293 7140 9857 0347 4373 8636 6947 1417 4698
0371 6233 2616 8045 6011 3661 9597 7424 7610 4281
根据以上数据统计该运动员射击4次至少击中3次的概率为( )
A.0.852 B.0.8192 C.0.8 D.0.75
14.若函数满足为自然对数底数),其中为的导函数,则当时,的取值范围是()
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,满分20分.把答案填写在答题纸相应的位置).
15.记函数的定义域为.在区间上随机取一个数,则的概率是.
16.若函数在上存在递增区间,则的取值范围是________.
17.设为抛物线的焦点,过且倾斜角为的直线交于,两点,则________.
18.已知点在曲线上,为曲线在点处的切线的倾斜角,则的取值范围是.
三、解答题(本大题共5小题,每小题12分,共60分.解答应写出文字说明,证明过程或演算步骤.)
19.某旅游爱好者计划从3个亚洲国家和3个欧洲国家中选择2个国家去旅游.
(Ⅰ)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;
(Ⅱ)若从亚洲国家和欧洲国家中各任选1个,求这2个国家包括但不包括的概率.
20.设函数,若函数在处与直线相切.
(Ⅰ)求实数的值;
(Ⅱ)求函数在上的最大值.
21.某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:,并整理得到如下频率分布直方图:
(Ⅰ)从总体的400名学生中随机抽取一人,估计其分数小于70的概率;
(Ⅱ)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)内的人数;
(Ⅲ)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等.试估计总体中男生和女生人数的比例.
22.设椭圆()的右焦点为,右顶点为,已知,其中为原点,为椭圆的离心率.
(Ⅰ)求椭圆的方程;
(Ⅱ)设过点的直线与椭圆交于点(不在轴上),垂直于的直线与交于点,与轴交于点,若,且,求直线的斜率.
23.已知.
(Ⅰ)对一切恒成立,求实数的取值范围;
(Ⅱ)证明:对一切,都有成立.
长安一中2017~2018学年度第一学期期末考试
高二数学(文科)参考答案及评分标准
一、选择题(本大题共14小题,每小题5分,共70分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
题号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
答案
A
C
D
B
B
A
A
C
A
C
B
D
D
C
二、填空题(本大题共4小题,每小题5分,满分20分.把答案填写在答题纸相应的位置).
15. 16. 17. 12 18.
三、解答题(本大题共5小题,每小题12分,共60分.解答应写出文字说明,证明过程或演算步骤.)
19.解:(1)由题意得,从6个国家中人员两个国家,其一切可能的结果组成基本事件有:
,,,,,
,,共15个. ………3分
所选两个国家都是亚洲的事件包含的基本事件有:,,,共3个,所以所求事件的概率为.……………………………………………………6分
(2)从亚洲国家和欧洲国家中任选一个,其一切可能的结果组成的基本事件有:
,,共9个,包含但不包含的事件所包含的基本事件有共2个.……10分
所以所求事件的概率为.……………………………………………………………12分
20.解:(1)由题意可得f′(x)=-2bx,………2分
∵函数f(x)在x=1处与直线y=-相切,
∴解得………6分
(2)由(1)知,f(x)=ln x-x2,则f′(x)=-x=,
当≤x≤e时,令f′(x)>0,得≤x<1,令f′(x)<0,得10),则h′(x)=,
当x∈(0,1)时,h′(x)<0,h(x)是减少的,当x∈(1,+∞)时,h′(x)>0,h(x)是增加的,
所以h(x)min=h(1)=4.
因为对一切x∈(0,+∞),2f(x)≥g(x)恒成立,所以a≤h(x)min=4.………5分
(2)证明:问题等价于xln x>-(x∈(0,+∞)).f(x)=xln x(x∈(0,+∞))的最小值是-,
当且仅当x=时取到,设m(x)=-(x∈(0,+∞)),则m′(x)=,
易知m(x)max=m(1)=-,当且仅当x=1时取到.
从而对一切x∈(0,+∞),都有ln x>-成立.………………………12分