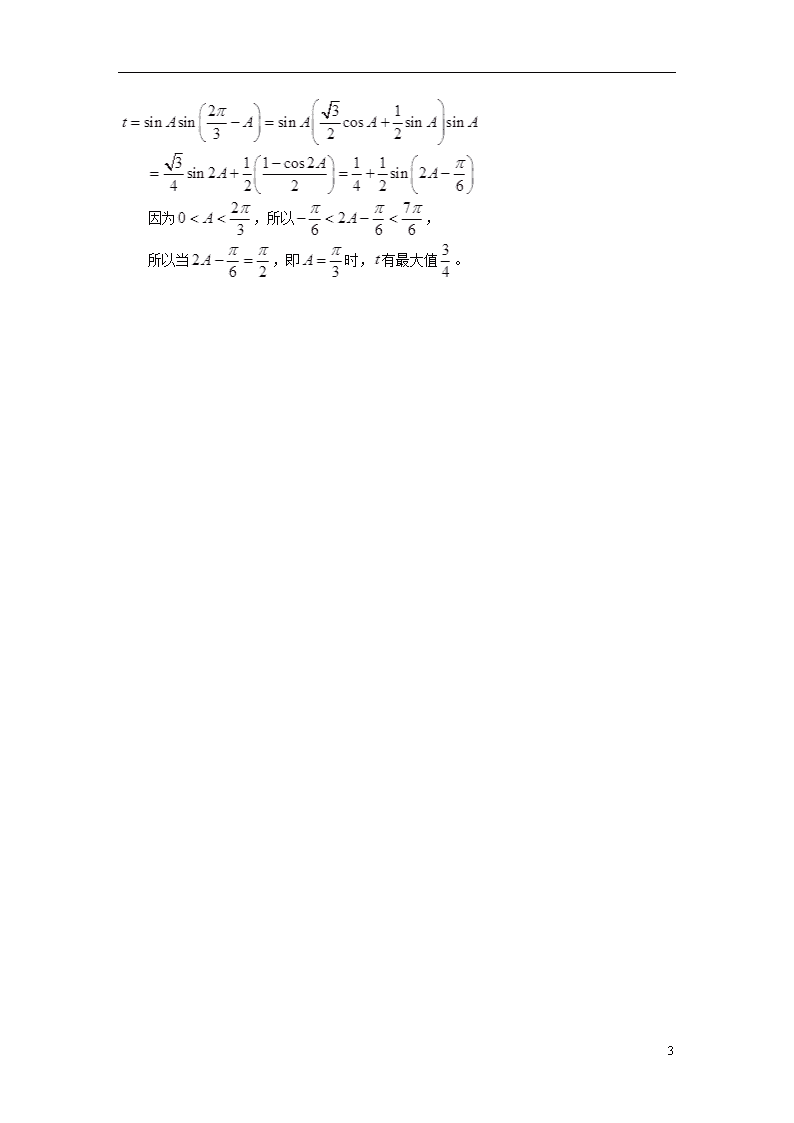- 136.50 KB
- 2021-04-14 发布
余弦定理
(答题时间:40分钟)
1. △ABC的内角的对边分别为,若成等比数列,且,则___________。
2. 在中,,则该三角形最大角的余弦值为__________。
3. 在△ABC中,设AD为BC边上的高,且AD=BC,b,c分别表示角B,C所对的边长,则的取值范围是____________。
4. 设△ABC的内角A,B,C所对的边分别为a,b,c。若(a+b-c)(a+b+c)=ab,则角C=________。
5. 在△ABC中,BC=,AC=1,以AB为边作等腰直角三角形ABD(B为直角顶点,C、D两点在直线AB的两侧)。当变化时,线段CD长的最大值为_________。
*6. 在△ABC中,角A,B,C所对的边分别为a,b,c,已知b=3,c=8,角A为锐角,△ABC的面积为6。
(1)求角A的大小;
(2)求a的值。
**7. 在中,角A、B、C的对边分别为a、b、c,且角A、B、C成等差教列。
(1)若,,求边c的值;
(2)设,求t的最大值。
3
1. 解:∵成等比数列,∴,又∵,∴,
∴。
2. 解:先由c2=a2+b2-2abcosC求出c=3,∴最大边为b,最大角为B,
∴cosB=。
3. 解:因为BC边上的高AD=BC=a,所以,则,又,
所以,
其中有tanA=2,又由基本不等式有所以的取值范围。
4. 解:所以
。
5. 解:设,,则在三角形BCD中,由余弦定理可知,在三角形ABC中,由余弦定理可知,可得,所以,令,则,当时等号成立,即CD长的最大值为3。
6. 解:(1)∵S△ABC=bcsinA=×3×8×sinA=6,∴sinA=,
∵A为锐角,∴A=。
(2)由余弦定理知a===7。
7. 解:(1)因为角成等差数列,所以,
因为,所以。
因为,,,
所以,
所以或(舍去)。
(2)因为,所以
3
因为,所以,
所以当,即时,有最大值。
3
相关文档
- 2020届一轮复习人教A版人教版高中2021-04-14 18:28:146页
- 2020-2021学年高中地理新教材中图2021-04-14 18:26:5315页
- 四川省绵阳市高中2017级第二次诊断2021-04-14 18:25:4614页
- 山东省2021年普通高中学业水平等级2021-04-14 18:25:229页
- 2018-2019学年吉林省长春市第十一2021-04-14 18:24:3819页
- 四川省绵阳市高中2020届高三高考适2021-04-14 18:24:0412页
- 2020_2021学年高中历史第五单元近2021-04-14 18:23:427页
- 湖北省武汉市部分市级示范高中20202021-04-14 18:23:1221页
- 2020暑假高中化学一轮复习:原子结构2021-04-14 18:22:135页
- 2019-2020学年人教版高中生物必修2021-04-14 18:22:037页