- 460.50 KB
- 2021-04-14 发布
2019—2020学年新疆昌吉州第一学期期末质量检测
高二数学(文科)试卷
一、单选题(12*5=60分)
1.已知,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
2.命题“”的否定是( )
A. B.
C. D.
3.抛物线的准线方程为( )
A. B. C. D.
4.椭圆与双曲线有相同的焦点,则的值是( )
A. B. C. D.不存在
5.已知双曲线的焦距为,则的离心率为
A. B. C. D.
6.椭圆的两焦点分别为F1,F2,以椭圆短轴的两顶点为焦点,长为虚轴长的双曲线方程为( )
A. B. C. D.
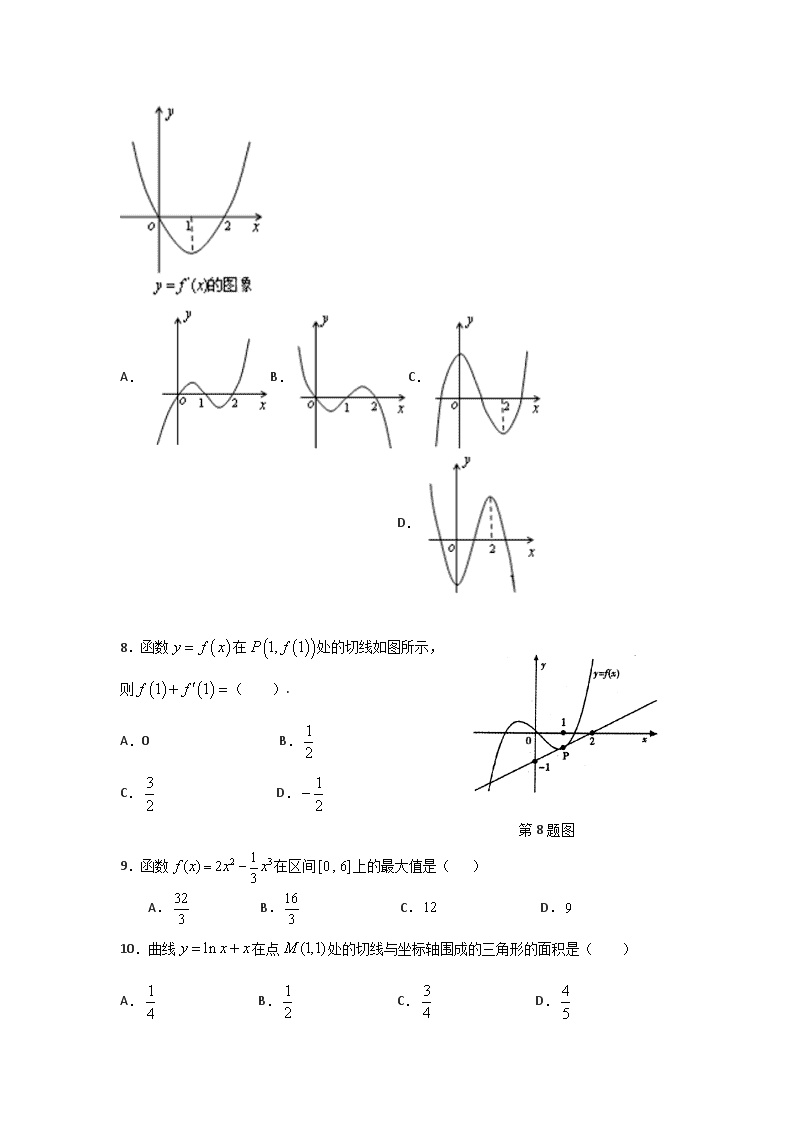
7.设是函数的导函数,的图象如图所示,则的图象最有可能的是( )
A.B.C. D.
8.函数在处的切线如图所示,
则( ).
A.0 B.
C. D.
第8题图
9.函数在区间上的最大值是( )
A. B. C. D.
10.曲线在点处的切线与坐标轴围成的三角形的面积是( )
A. B. C. D.
11.已如函数f(x),则f′(π)+f′(﹣π)=( )
A.﹣2 B.2 C. D.0
12.直线交椭圆于两点,若线段中点的横坐标为1,则( )
A.-2 B.-1 C.1 D.2
二、填空题(4*5=20分)
13.“”是“”的___________条件.
14.已知椭圆的左右焦点分别为,,过右焦点的直线AB与椭圆交于A,B两点,则的周长为______.
15.以为渐近线且经过点的双曲线方程为______.
16.函数在处的切线方程是________.
三、解答题(17题10分,18、19、20、21、22题各12分,共70分)
17.已知抛物线的准线方程为.
(Ⅰ)求的值;
(Ⅱ)直线交抛物线于、两点,求弦长.
18.已知 ,:关于的方程有实数根.
(1)若为真命题,求实数的取值范围;
(2)若为真命题,为真命题,求实数的取值范围.
19.设点是椭圆上一动点,椭圆的长轴长为,离心率为.
(1)求椭圆的方程;
(2)求点到直线距离的最大值.
20.已知:双曲线.
(1)求双曲线的焦点坐标、顶点坐标、离心率;
(2)若一条双曲线与已知双曲线有相同的渐近线,且经过点,求该双曲线的方程.
21.求下列函数的导数.
(1)y=3x2+xcos x;
(2)f(x)= .
22.设函数
(1)求的单调区间;
(2)求函数在区间上的最小值。
参考答案
1.A
2.C
3.D
4.A
5.C
6.B
7.C
8.A
9.A
10.A
11.D
12.A
13.充分非必要
14.16
15.
16.
17.(Ⅰ)2;(Ⅱ)8.
18.(1);(2)
19.(1);(2)
20.(1)焦点,顶点,离心率;(2)
21.(1)f’(x)=6x+cos x –xsin x(2);
22.(1) (2)1