- 910.51 KB
- 2021-04-14 发布
提分微课(六)
利用“胡不归、阿氏圆”解决
“
PA
+
n·PB
”
型的最值问题
第七单元 图形的变化
“
胡不归
”
和
“
阿氏圆
”
问题都是一类解决
“
PA
+
n
·
PB
”(
n
为常数且
n
≠1)
型的最值问题
.
两类问题所蕴含的都是数学的转化思想
,
即将
nPB
的长度转化为某条具体线段
PC
的长度
,
进而根据
“
垂线段最短或两点之间线段最短
”
的原理构造最短距离
.
动点
P
在直线上运动的可用
“
胡不归
”
问题模型
,
动点
P
在圆周上运动的可用
”
阿氏圆
”
问题模型
.
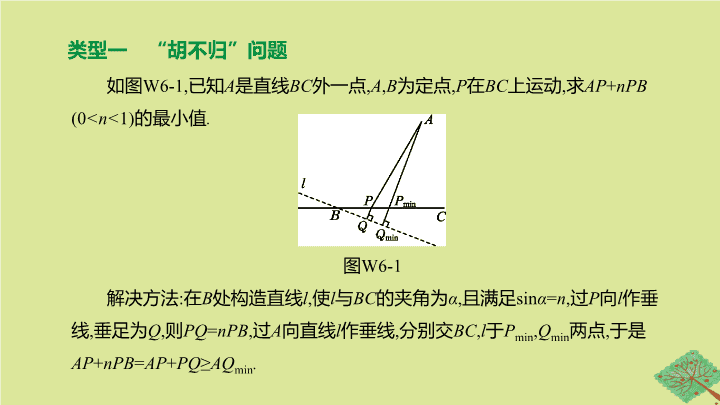
类型一 “胡不归”问题
如图
W6-1,
已知
A
是直线
BC
外一点
,
A
,
B
为定点
,
P
在
BC
上运动
,
求
AP
+
nPB
(0