- 4.31 MB
- 2021-04-14 发布
2017-2018学年度石嘴山三中12月月考数学理科试卷
考试时间:120分钟;命题人: 2017-12-11
第I卷(选择题)
一、选择题(每小题5分)
1.设, , ,则( )
A. B. C. D.
2.复数的共轭复数是( )
A. B. C. D.
3.命题“”是命题“直线与直线平行”的( )
A. 充要条件 B. 充分不必要条件
C. 必要不充分条件 D. 即不充分也不必要条件
4.《张丘建算经》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有女不善织,日减功迟,初日织五尺,末日织一尺,今共织九十尺,问织几日?”,已知“日减功迟”的具体含义是每天比前一天少织同样多的布,则此问题的答案是( )
A. 10日 B. 20日 C. 30日 D. 40日
5.已知向量a与b的夹角是,且|a|=1,|b|=4,若(3a+λb)⊥a,则实数λ=
A. B. C. -2 D. 2
6.已知,给出下列四个命题:( )
A. , B. , C. , D. ,
7.已知定义在上的函数的周期为,当时, ,
则( )
A. B. C. D.
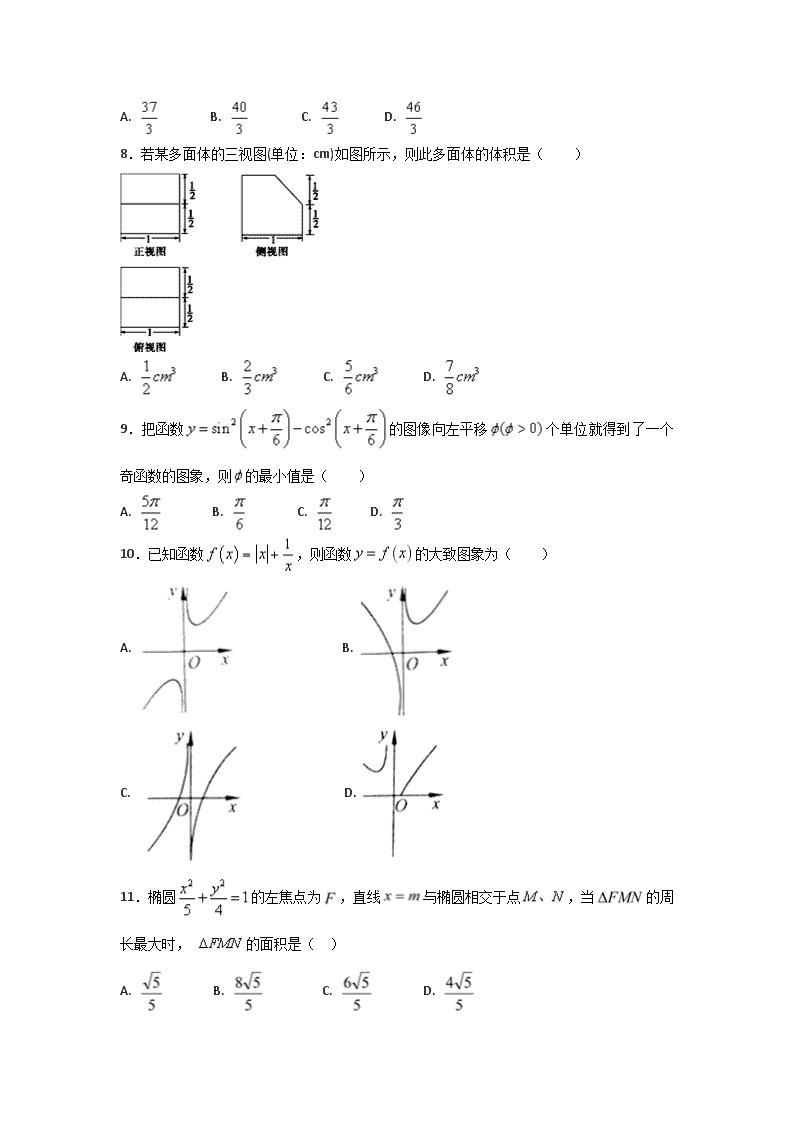
8.若某多面体的三视图(单位:cm)如图所示,则此多面体的体积是( )
A. B. C. D.
9.把函数的图像向左平移个单位就得到了一个奇函数的图象,则的最小值是( )
A. B. C. D.
10.已知函数,则函数的大致图象为( )
A. B.
C. D.
11.椭圆的左焦点为,直线与椭圆相交于点,当的周长最大时, 的面积是( )
A. B. C. D.
12.给定方程:,给出下列4个结论:
①该方程没有小于0的实数解;
②该方程有无数个实数解;
③该方程在内有且只有一个实数根;
④若是方程的实数根,则. 其中正确结论的个数是( )
A.1 B.2 C. 3 D. 4
二、填空题(每小题5分)
13.若等比数列的前5项的乘积为1, ,则数列的公比为( )
14.已知抛物线上横坐标为 3 的点到其焦点的距离为 4,则________.
15.已知平面向量与是共线向量且,则_________.
16.刘徽(约公元 225 年—295 年)是魏晋时期伟大的数学家,中国古典数学理论的奠基人之一,他的杰作《九章算术注》和《海岛算经》是中国宝贵的古代数学遗产. 《九章算术·商功》中有这样一段话:“斜解立方,得两壍堵. 斜解壍堵,其一为阳马,一为鳖臑.” 刘徽注:“此术臑者,背节也,或曰半阳马,其形有似鳖肘,故以名云.” 其实这里所谓的“鳖臑(biē nào)”,就是在对长方体进行分割时所产生的四个面都为直角三角形的三棱锥. 如图,在三棱锥中, 垂直于平面, 垂直于,且 ,则三棱锥的外接球的球面面积为__________.
三、解答题
17.(12分)在△ABC中,内角A,B,C所对的边分别为a,b,c.已知a-c=b,
sinB=sinC.
(1)求cosA的值;
(2)求cos的值.
18.(12分)某花店每天以每枝元的价格从农场购进若干枝玫瑰花,然后以每枝元的价格出售.如果当天卖不完,剩下的玫瑰花做垃圾处理.
(1)若花店一天购进枝玫瑰花,求当天的利润(单位:元)关于当天需求量(单位:枝, )的函数解析式.
(2)花店记录了天玫瑰花的日需求量(单位:枝),整理得下表:
日需求量
频数
假设花店在这天内每天购进枝玫瑰花,求这天的日利润(单位:元)的平均数.
19.(12分)如图,在直三棱柱中,底面是等腰直角三角形, ,侧棱,点分别为棱的中点, 的重心为,直线垂直于平面.
(1)求证:直线平面;
(2)求二面角的余弦.
20.(12分)已知椭圆: 的左、右焦点分别为 且离心率为, 为椭圆上三个点, 的周长为,线段的垂直平分线经过点.
(1)求椭圆的方程;
(2)求线段长度的最大值.
21.(12分)已知函数.
(1)若,求曲线在点处的切线方程;
(2)若曲线与直线只有一个交点,求实数的取值范围.
22.(10分)已知函数,且的解集为.
(1)求的值;
(2)若为正数,且,求证.
2017-2018学年度石嘴山三中12月月考数学理科试卷答案
考试时间:120分钟;命题人:
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
一、选择题
1.设, , ,则( )
A. B. C. D.
【答案】C
2.复数的共轭复数是( )
A. B. C. D.
【答案】A
3.命题“”是命题“直线与直线平行”的( )
A. 充要条件 B. 充分不必要条件
C. 必要不充分条件 D. 即不充分也不必要条件
【答案】A
4.《张丘建算经》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有女不善织,日减功迟,初日织五尺,末日织一尺,今共织九十尺,问织几日?”,已知“日减功迟”的具体含义是每天比前一天少织同样多的布,则此问题的答案是( )
A. 10日 B. 20日 C. 30日 D. 40日
【答案】B
5.已知向量a与b的夹角是,且|a|=1,|b|=4,若(3a+λb)⊥a,则实数λ=
A. B. C. -2 D. 2
【答案】A
6.已知,给出下列四个命题:( )
A. , B. , C. , D. ,
【答案】D
7.已知定义在上的函数的周期为,当时, ,
则
A. B. C. D.
【答案】C
。
8.若某多面体的三视图(单位:cm)如图所示,则此多面体的体积是( )
A. B. C. D.
【答案】D
【解析】由三视图可知该几何体为上部是一平放的直五棱柱,柱体高h=1.侧视图为其底面.
底面多边形可看作边长为1的正方形截去直角边为的等腰直角三角形而得到,其面积
S=1×1﹣= 。
所以几何体体积V=Sh=1×= 。
故答案为:D。
9.把函数的图像向左平移个单位就得到了一个奇函数的图象,则的最小值是( )
A. B. C. D.
【答案】C
【解析】函数 ,向左平移后得到是奇函数,则当x=0时,y=0,代入得到,则此时的最小值是。
故答案选C。
10.已知函数,则函数的大致图象为
A. B.
C. D.
【答案】B
11.椭圆的左焦点为,直线与椭圆相交于点,当
的周长最大时, 的面积是( )
A. B. C. D.
【答案】B
【解析】设右焦点为,连接当直线过右焦点时, 的周长最大,由椭圆的定义可得: 的周长的最大值, ,把代入椭圆标准方程得: ,解得此时的面积,故选B.
12.给定方程:,给出下列4个结论:
①该方程没有小于0的实数解;
②该方程有无数个实数解;
③该方程在内有且只有一个实数根;
④若是方程的实数根,则.
其中正确结论的个数是( )
A.1 B.2 C. 3 D. 4
【答案】C
二、填空题
13.若等比数列的前5项的乘积为1, ,则数列的公比为( )
【答案】2
14.已知抛物线上横坐标为 3 的点到其焦点的距离为 4,则________.
【答案】2
【解析】抛物线y2=2px(p>0)的准线方程为: ,
∵抛物线y2=2px(p>0)上横坐标为3的点到焦点的距离等于4,
∴根据抛物线的定义可知,
∴p=2.
故答案为2.
15.已知平面向量与是共线向量且,则_________.
【答案】
【解析】∵平面向量=(2m+1,3),=(2,m),且与反向,
∴m(2m+1)﹣3×2=0,
解得m=﹣2,或m=;
验证m=时不满足题意,
∴=(2,﹣2);
∴||=2.
16.刘徽(约公元 225 年—295 年)是魏晋时期伟大的数学家,中国古典数学理论的奠基人之一,他的杰作《九章算术注》和《海岛算经》是中国宝贵的古代数学遗产. 《九章算术·商功》中有这样一段话:“斜解立方,得两壍堵. 斜解壍堵,其一为阳马,一为鳖臑.” 刘徽注:“此术臑者,背节也,或曰半阳马,其形有似鳖肘,故以名云.” 其实这里所谓的“鳖臑(biē nào)”,就是在对长方体进行分割时所产生的四个面都为直角三角形的三棱锥. 如图,在三棱锥中, 垂直于平面, 垂直于,且 ,则三棱锥的外接球的球面面积为__________.
【答案】
【解析】由条件知道垂直于平面, 垂直于,故AB垂直于,从而得到垂直于面ABC,故三角形ABD和三角形ACD都是直角三角形,则外接球球心在AD的中点上,记作O点,
表面积是
故结果为:
三、解答题
17.在△ABC中,内角A,B,C所对的边分别为a,b,c.已知a-c=b,sinB=sinC.
(1)求cosA的值;
(2)求cos的值.
【答案】(1) (2)
【解析】试题分析:(1)先根据正弦定理得b=c.再利用余弦定理求cosA的值;(2)根据同角三角函数关系得sinA,根据二倍角公式得cos2A,sin2A,最后根据两角差余弦公式求结果
试题解析:(1)在△ABC中,由sinB=sinC.可得b=c.
又由a-c=b,有a=2c.
所以cosA=
(2)在△ABC中,由cosA=,可得sinA=.
于是,cos2A=2cos2A-1=-,sin2A=2sinA·cosA=.
所以cos.
18.某花店每天以每枝元的价格从农场购进若干枝玫瑰花,然后以每枝元的价格出售.如果当天卖不完,剩下的玫瑰花做垃圾处理.
(1)若花店一天购进枝玫瑰花,求当天的利润(单位:元)关于当天需求量(单位:枝, )的函数解析式.
(2)花店记录了天玫瑰花的日需求量(单位:枝),整理得下表:
日需求量
频数
假设花店在这天内每天购进枝玫瑰花,求这天的日利润(单位:元)的平均数.
【答案】(1);(2).
【解析】试题分析:(1)根据卖出一枝可得利润元,卖不出一枝可得赔本元,以花店一天购进枝玫瑰花为分点即可建立分段函数;(2)根据表格中的数据,讨论需求量得到这天的日利润的平均数,利用天的销售量除以即可得到结论.
试题解析:(1)当日需求量时,利润,
当日需求量时,利润,
所以.
(2)当时,利润;当时,利润;
当时,利润;当时,利润;
当时,利润;当时,利润;
当时,利润;
所以日利润的平均数(元).
19.如图,在直三棱柱中,底面是等腰直角三角形, ,侧棱,点分别为棱的中点, 的重心为,直线垂直于平面.
(1)求证:直线平面;
(2)求二面角的余弦.
【答案】(1)证明见解析;(2) .
(1) 连结 ,则在三角形中为中位线,于是,
因为为中点,所以平行且等于. 所以在平行四边形中, 平行于
因为在平面 上,所以平行于平面
(2)分别以为轴建立空间直角坐标系
设,则
因为垂直于平面,所以有,
解得,所以
面的法向量,面的法向量为
所以
结合图形知,二面角的预先为.
20.已知椭圆: 的左、右焦点分别为 且离心率为,
为椭圆上三个点, 的周长为,线段的垂直平分线经过点.
(1)求椭圆的方程;
(2)求线段长度的最大值.
【答案】(1) ;(2)4.
(1),
,
所以椭圆的方程为.
(2)当斜率不存在时, 最大值为
当斜率存在时,设:
联立与得: ,
中点坐标为
因为的垂直平分线经过点,所以(若为0,则中垂线为轴,这与题意不符)
化简得:
所以
所以最大值为4.
21.已知函数.
(1)若,求曲线在点处的切线方程;
(2)若曲线与直线只有一个交点,求实数的取值范围.
【答案】(1);(2).
【解析】
试题解析:(1),,,所以切线方程为.
(2)曲线与直线只有一个交点,等价于关于的方程只有一个实根.
显然,所以方程只有一个实根.
设函数,则.
设,,为增函数,又.
所以当时,,为增函数;
当时,,为减函数;
当时,,为增函数;
所以在时取极小值.
又当趋向于时,趋向于正无穷;
又当趋向于负无穷时,趋向于负无穷;
又当趋向于正无穷时,趋向于正无穷.所以图象大致如图所示:
所以方程只有一个实根时,实数的取值范围为.
22.在平面直角坐标系中,以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,直线上两点的极坐标分别为.圆的参数方程为(为参数).
(1)设为线段的中点,求直线 的平面直角坐标方程;
(2)判断直线与圆的位置关系.
【答案】(1) ;(2) 与相交.
【解析】试题分析:(1)根据极值互化的公式得到的平面直角坐标为,再根据中点坐标公式得到的坐标为(2)根据参普互化的公式得到直线的一般方程,在比较圆心到直线的距离的大小关系,从而得到直线和圆的位置关系.
(1)的平面直角坐标为
于是的坐标为
所以的平面直角坐标方程为:
(2)直线的方程为:
圆的方程为: ,
到的距离
所以与相交.
23.已知函数,且的解集为.
(1)求的值;
(2)若为正数,且,求证.
【答案】(1) ;(2)证明见解析.
(1),
设,则当时, ;
当时, ;
当时,
所以.
(2)
由柯西不等式,
所以.