- 846.00 KB
- 2021-04-14 发布
2019-2020学年甘肃省武威市第六中学高一上学期第一次段考数学试题
一、单选题
1.已知全集U={1,2,3,4,5},且A={2,3,4},B={4,5},则等于( )
A.{4} B.{4,5} C.{1,2,3,4} D.{2,3}
【答案】D
【解析】【详解】试题分析:由题={1,2,3},所以{2,3},故选D.
【考点】集合的运算
2.函数的图象是( )
A. B. C. D.
【答案】C
【解析】利用函数图像上两个点,选出正确选项.
【详解】
由于函数经过点,只有C选项符合.
故选:C.
【点睛】
本小题主要考查函数图像的识别,属于基础题.
3.已知集合,,则实数值为( )
A.4 B.3 C.2 D.1
【答案】B
【解析】因为集合,,故必有m+1=4,m=3,选B
4.已知集合A到B的映射f:x→y=2x+1,那么集合A中元素2在B中的象是( )
A.5 B.2 C.6 D.8
【答案】A
【解析】【详解】
,
,
所以 ,
集合A中元素2在B中的象是5,
故选A.
5.,,的大小关系是( )
A. B. C. D.
【答案】D
【解析】将、、均化为的指数幂,然后利用指数函数的单调性可得出、、的大小关系.
【详解】
,,,
且指数函数在上是增函数,则,因此,.
故选:D.
【点睛】
本题考查指数幂的大小比较,考查指数函数单调性的应用,解题的关键就是将三个数化为同一底数的指数幂,考查分析问题和解决问题的能力,属于中等题.
6.函数f(x)=+的定义域为( )
A. B. C. D.
【答案】C
【解析】根据分母部位0,被开方数大于等于0构造不等式组,即可解出结果.
【详解】
利用定义域的定义可得 ,解得,即,
故选C.
【点睛】
本题考查定义域的求解,需掌握:
分式分母不为0,②偶次根式被开方数大于等于0,③对数的真数大于0.
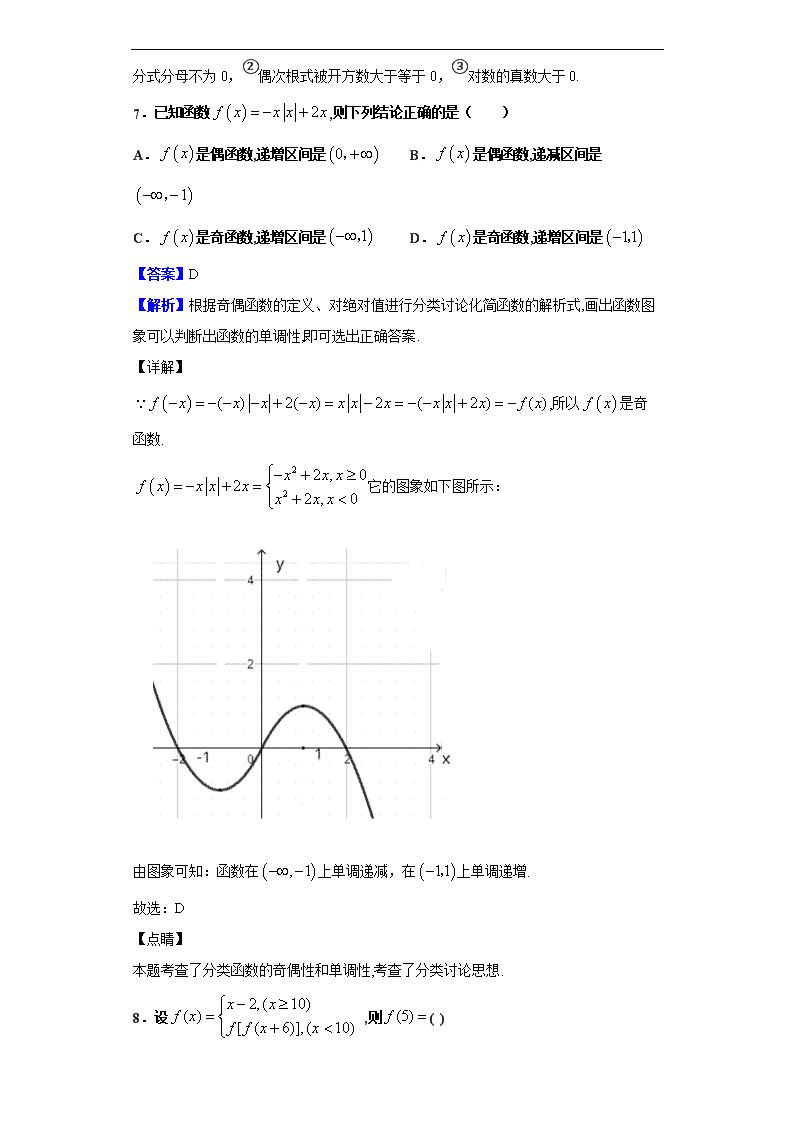
7.已知函数,则下列结论正确的是( )
A.是偶函数,递增区间是 B.是偶函数,递减区间是
C.是奇函数,递增区间是 D.是奇函数,递增区间是
【答案】D
【解析】根据奇偶函数的定义、对绝对值进行分类讨论化简函数的解析式,画出函数图象可以判断出函数的单调性,即可选出正确答案.
【详解】
,所以是奇函数.
它的图象如下图所示:
由图象可知:函数在上单调递减,在上单调递增.
故选:D
【点睛】
本题考查了分类函数的奇偶性和单调性,考查了分类讨论思想.
8.设 ,则( )
A.10 B.11 C.12 D.13
【答案】B
【解析】根据题中给出的分段函数,只要将问题转化为求x≥10内的函数值,代入即可求出其值.
【详解】
∵f(x),
∴f(5)=f[f(11)]
=f(9)=f[f(15)]
=f(13)=11.
故选:B.
【点睛】
本题主要考查了分段函数中求函数的值,属于基础题.
9.已知函数是定义在R上的奇函数,若则( )。
A. B. C. D.
【答案】C
【解析】由题意可求得,由题意函数是定义在R上的奇函数,利用奇函数的定义,可推出,从而求解出的值。
【详解】
,可得
又因为函数是定义在R上的奇函数,可知,
所以,故答案选C。
【点睛】
本题主要考查利用函数的奇偶性求值,解题的关键是要对已知式进行变形,将未知化为已知。
10.指数函数y=ax在[0,1]上的最大值与最小值的和为3,则函数y=2ax-1在[0,1]上的最大值是( )
A.6 B.3 C.1 D.
【答案】B
【解析】根据指数函数的底数的不同的取值范围进行分类讨论,结合题意求出的值,然后利用一次函数的单调性求出函数y=2ax-1在[0,1]上的最大值.
【详解】
当时,指数函数y=ax是单调递增函数,因此当指数函数y=ax在[0,1]上的最大值与最小值分别是,由题意可知:,所以函数在[0,1]上的最大值为:
;
当时,指数函数y=ax是单调递减函数,因此当指数函数y=ax在[0,1]上的最大值与最小值分别是,由题意可知:舍去.
故选:B
【点睛】
本题考查了指数函数的单调性和一次函数的单调性,考查了分类思想,考查了数学运算能力.
11.已知为二次函数,且满足,,则的解析式为( )
A. B.
C. D.
【答案】A
【解析】设出二次函数的解析式,结合已知利用待定系数法可以求出的解析式.
【详解】
设,因为,所以.
又,所以有
,解得
.
故选:A
【点睛】
本题考查了用待定系数法求二次函数解析式,考查了数学运算能力.
12.设函数则满足f(x+1)0,x1+x2<0,.
∴f(x1)-f(x2)<0,即f(x1)