【数学】2018届一轮复习人教A版8-7利用空间向量求空间角学案 26页

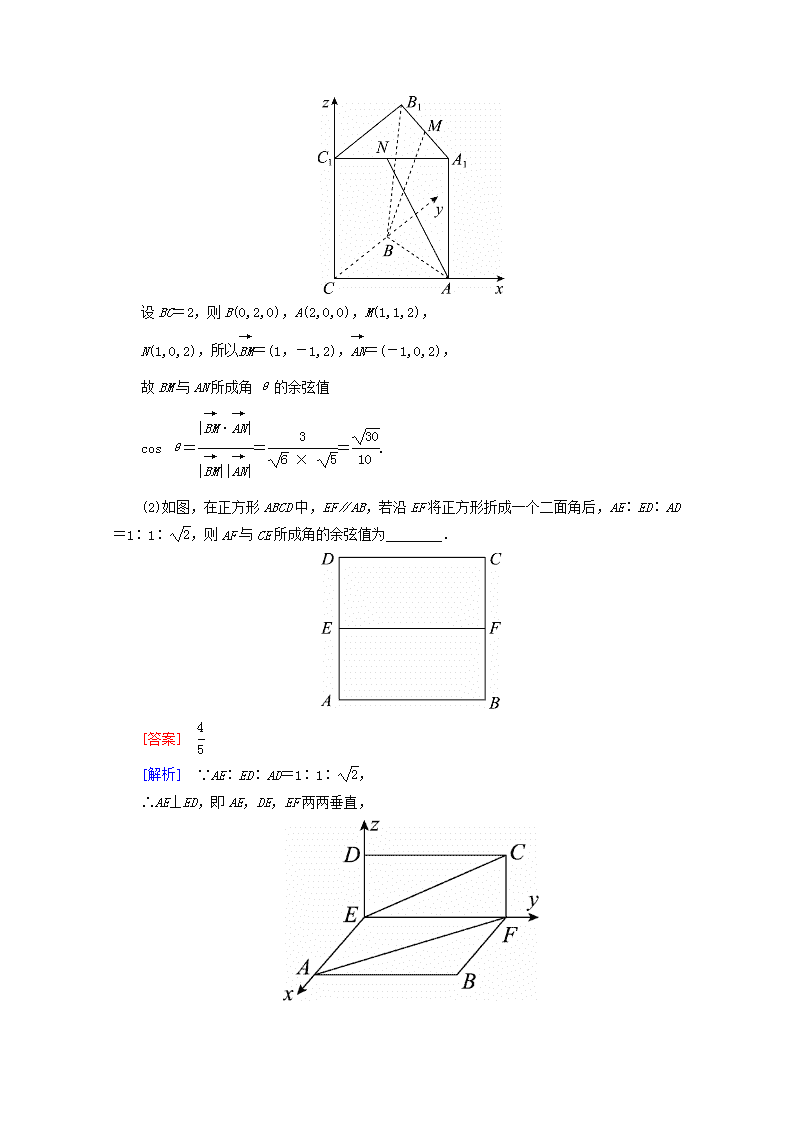
‎§8.7　利用空间向量求空间角 考纲展示►　‎ ‎1.能用向量方法解决直线与直线、直线与平面、平面与平面的夹角的计算问题.‎ ‎2.了解向量方法在研究立体几何问题中的应用.‎ 考点1　异面直线所成的角 两条异面直线所成角的求法 设两条异面直线a，b的方向向量为a，b，其夹角为θ，则cos φ＝|cos θ|＝(其中φ为异面直线a，b所成的角)．‎ 空间角的范围处理错误．‎ 已知向量m，n分别是直线l和平面α的方向向量、法向量，若cos〈m，n〉＝－，则l与α所成的角为________．‎ 答案：30°‎ 解析：设l与α所成的角为θ，‎ 则sin θ＝|cos〈m，n〉|＝，∴θ＝30°.‎ ‎[典题1]　(1)直三棱柱ABC－A1B‎1C1中，∠BCA＝90°，M，N分别是A1B1，A‎1C1的中点，BC＝CA＝CC1，则BM与AN所成角的余弦值为(　　)‎ A. B. C. D. 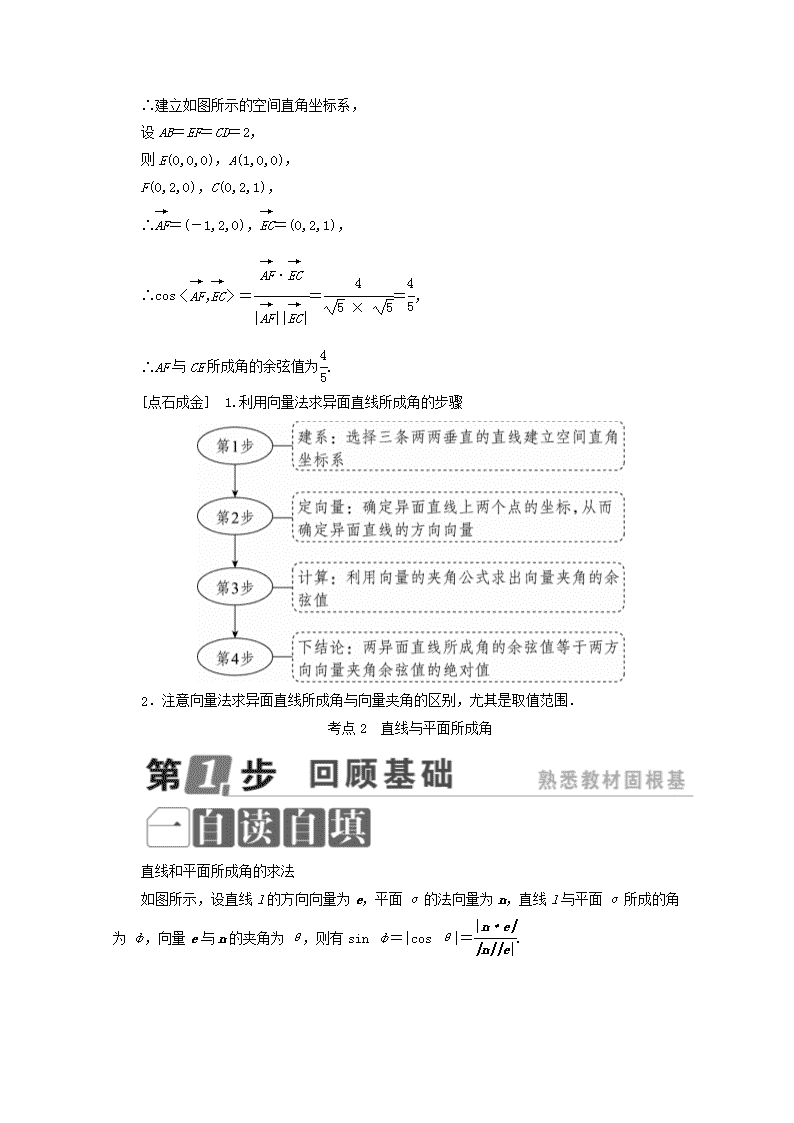‎[答案]　C ‎[解析]　建立如图所示的空间直角坐标系C－xyz，‎ 设BC＝2，则B(0,2,0)，A(2,0,0)，M(1,1,2)，‎ N(1,0,2)，所以＝(1，－1,2)，＝(－1,0,2)，‎ 故BM与AN所成角θ的余弦值 cos θ＝＝＝.‎ ‎(2)如图，在正方形ABCD中，EF∥AB，若沿EF将正方形折成一个二面角后，AE∶ED∶AD＝1∶1∶，则AF与CE所成角的余弦值为________．‎ ‎[答案]　 ‎[解析]　∵AE∶ED∶AD＝1∶1∶，‎ ‎∴AE⊥ED，即AE，DE，EF两两垂直，‎ ‎∴建立如图所示的空间直角坐标系，‎ 设AB＝EF＝CD＝2，‎ 则E(0,0,0)，A(1,0,0)，‎ F(0,2,0)，C(0,2,1)，‎ ‎∴＝(－1,2,0)，＝(0,2,1)，‎ ‎∴cos〈，〉＝＝＝，‎ ‎∴AF与CE所成角的余弦值为.‎ ‎[点石成金]　1.利用向量法求异面直线所成角的步骤 ‎2．注意向量法求异面直线所成角与向量夹角的区别，尤其是取值范围．‎ 考点2　直线与平面所成角 ‎ 　‎ 直线和平面所成角的求法 如图所示，设直线l的方向向量为e，平面α的法向量为n，直线l与平面α所成的角为φ，向量e与n的夹角为θ，则有sin φ＝|cos θ|＝.‎ ‎(1)[教材习题改编]若直线l的方向向量与平面α的法向量的夹角等于120°，则直线l与平面α所成的角等于________．‎ 答案：30°‎ 解析：根据线面角的定义易知为30°.‎ ‎(2)[教材习题改编]如果平面的一条斜线和它在这个平面上的射影的方向向量分别是a＝(0,2,1)，b＝(，，)，那么这条斜线与平面的夹角是________．‎ 答案：30°‎ 解析：cos〈a，b〉＝＝，因此a与b的夹角为30°，即斜线与平面的夹角也为30°.‎ ‎(3)[教材习题改编]如图所示，在正方体ABCD－A1B‎1C1D1中，M，N分别为棱AA1和BB1的中点，则sin〈，〉的值为________．‎ 答案： 解析：设正方体的棱长为2，以D为坐标原点，，，所在方向分别为x轴、y轴、z轴的正方向建立空间直角坐标系，可知＝(2，－2,1)，＝(2,2，－1)，所以cos〈，〉＝－‎ ，所以sin〈，〉＝.‎ ‎[典题2]　[2017·河南郑州二模]如图，在三棱柱ABC－A1B‎1C1中，四边形AA‎1C1C是边长为2的菱形，平面ABC⊥平面AA‎1C1C，∠A‎1AC＝60°，∠BCA＝90°. ‎ ‎(1)求证：A1B⊥AC1；‎ ‎(2)已知点E是AB的中点，BC＝AC，求直线EC1与平面ABB‎1A1所成的角的正弦值．‎ ‎(1)[证明]　AC的中点O，连接A1O，‎ 因为四边形AA‎1C1C是菱形，且∠A‎1AC＝60°，‎ 所以△A‎1AC为等边三角形，所以A1O⊥AC.‎ 又平面ABC⊥平面AA‎1C1C，‎ 所以A1O⊥平面ABC，所以A1O⊥BC.‎ 又BC⊥AC，所以BC⊥平面AA‎1C1C，‎ 所以AC1⊥BC.‎ 在菱形AA‎1C1C中，AC1⊥A‎1C，‎ 所以AC1⊥平面A1BC，‎ 所以A1B⊥AC1.‎ ‎(2)[解]　以点O为坐标原点，建立如图所示的空间直角坐标系O－xyz，‎ 则A(0，－1,0)，B(2,1,0)，C(0,1,0)，C1(0,2，)，‎ ＝(2,2,0)，＝＝(0,1，)．‎ 设m＝(x，y，z)是平面ABB‎1A1的法向量，‎ 则即 取z＝－1，可得m＝(－，，－1)．‎ 又E(1,0,0)，所以＝(－1,2，)，‎ 设直线EC1与平面ABB‎1A1所成的角为θ，‎ 则sin θ＝|cos〈，m〉|＝＝.‎ ‎[点石成金]　利用向量法求线面角的方法 ‎(1)分别求出斜线和它在平面内的射影直线的方向向量，转化为求两个方向向量的夹角(或其补角)．‎ ‎(2)通过平面的法向量来求，即求出斜线的方向向量与平面的法向量所夹的锐角，取其余角就是斜线和平面所成的角.‎ ‎[2017·辽宁协作体联考]在正方体ABCD－A1B‎1C1D1中，求BB1与平面ACD1所成的角的余弦值．‎ 解：设正方体的边长为DD1＝1，‎ 分别以DA，DC，DD1所在直线为x轴、y轴、z轴建立空间直角坐标系，‎ 则有D(0,0,0)，A(1,0,0)，B(1,1,0)，C(0,1,0)，‎ D1(0,0,1)，B1(1,1,1)，‎ 则＝(0,0,1)，＝(－1,0,1)，‎ ＝(－1,1,0)．‎ 设n＝(x，y，z)为平面ACD1的法向量，‎ 则有即 取x＝1，得n＝(1,1,1)．‎ 设直线BB1与平面ACD1所成的角为α，‎ 则有sin α＝|cos〈n，〉|＝＝，‎ 故cos α＝＝.‎ 即BB1与平面ACD1所成角的余弦值为.‎ 考点3　二面角 求二面角的大小 ‎(1)如图①，AB，CD是二面角α－l－β的两个面内与棱l垂直的直线，则二面角的大小θ＝________.‎ ‎　‎ 答案：〈，〉‎ ‎(2)如图②③，n1，n2分别是二面角α－l－β的两个半平面α，β 的法向量，则二面角的大小θ＝〈n1，n2〉或π－〈n1，n2〉．‎ 二面角的求法：可先求出两个平面的法向量n1，n2所成的角〈n1，n2〉，则所求二面角为〈n1，n2〉或π－〈n1，n2〉．‎ 已知ABCD－A1B‎1C1D1是棱长为6的正方体，E，F分别是棱AB，BC上的动点，且AE＝BF.当A1，E，F，C1共面时，平面A1DE与平面C1DF所成二面角的余弦值为________．‎ 答案： 解析：以D为原点，，，所在直线分别为x轴、y轴、z轴建立空间直角坐标系，如图所示，‎ 易知当E(6,3,0)，F(3,6,0)时，A1，E，F，C1四点共面．设平面A1DE的法向量为n1＝(a，b，c)，依题意得 可取n1＝(－1,2,1)．同理可得平面C1DF的一个法向量为n2＝(2，－1,1)．故平面A1DE与平面C1DF所成二面角的余弦值为＝.‎ ‎[典题3]　如图，四棱柱ABCD－A1B‎1C1D1的所有棱长都相等，AC∩BD＝O，A‎1C1∩B1D1＝O1，‎ 四边形ACC‎1A1和四边形BDD1B1均为矩形．‎ ‎(1)求证：O1O⊥底面ABCD；‎ ‎(2)若∠CBA＝60°，求二面角C1－OB1－D的余弦值．‎ ‎(1)[证明]　因为四边形ACC‎1A1为矩形，‎ 所以CC1⊥AC，同理DD1⊥BD.‎ 因为CC1∥DD1，‎ 所以CC1⊥BD，而AC∩BD＝O，‎ 因此CC1⊥底面ABCD.‎ 由题设知，O1O∥C‎1C，‎ 故O1O⊥底面ABCD.‎ ‎(2)[解]　因为四棱柱ABCD－A1B‎1C1D1的所有棱长都相等，‎ 所以四边形ABCD是菱形，因此AC⊥BD.‎ 又O1O⊥底面ABCD，从而OB，OC，OO1两两垂直．‎ 如图，以O为坐标原点，OB，OC，OO1所在直线分别为x轴、y轴、z轴，建立空间直角坐标系O－xyz.‎ 不妨设AB＝2，因为∠CBA＝60°，‎ 所以OB＝，OC＝1.‎ 于是相关各点的坐标为O(0,0,0)，B1(，0,2)，C1(0,1,2)．‎ 易知n1＝(0,1,0)是平面BDD1B1的一个法向量. ‎ 设n2＝(x，y，z)是平面OB‎1C1的法向量，‎ 则即 取z＝－，则x＝2，y＝2，‎ 所以n2＝(2,2，－)．‎ 设二面角C1－OB1－D的大小为θ，易知θ是锐角，‎ 于是cos θ＝|cos〈n1，n2〉|＝＝＝.‎ 故二面角C1－OB1－D的余弦值为.‎ ‎[题点发散1]　将(2)中条件“∠CBA＝60°”改为“∠CBA＝90°”，问题不变．‎ 解：由母题(2)建系条件知，当∠CBA＝90°时，四边形ABCD为正方形，‎ 不妨设AB＝2，则OB＝，OC＝，‎ ‎∴O(0,0,0)，B1(，0,2)，C1(0，，2)．‎ 易知n1＝(0,1,0)是平面OB1D的一个法向量．‎ 设n2＝(x，y，z)是平面OB‎1C1的法向量，‎ 则即 取z＝－，则x＝2，y＝2，则n2＝(2,2，－)．‎ 设二面角C1－OB1－D为θ，‎ 则cos θ＝|cos〈n1，n2〉|＝＝，‎ 故二面角C1－OB1－D的余弦值为.‎ ‎[题点发散2]　在题干条件下，试在线段C‎1C上求一点M，使二面角 M－OB1－D的大小为60°.‎ 解：在母题(2)建系条件下，O(0,0,0)，B1(，0,2)，C1(0,1,2)．‎ 易知n1＝(0,1,0)是平面OB1D的一个法向量．‎ 设M(0,1，m)，且n2＝(x，y，z)是平面OB‎1M的一个法向量．‎ 则即 取z＝－1，则x＝，y＝m，‎ 则n2＝.‎ 由cos〈n1，n2〉＝知，＝，‎ ‎∴m2＝(m>0)，即m＝，‎ ‎∴M.‎ 即在线段CC1上存在一点M且CM＝，使二面角M－OB1－D的大小为60°.‎ ‎[点石成金]　1.利用向量计算二面角大小的常用方法 ‎(1)找法向量法：分别求出二面角的两个半平面所在平面的法向量，然后通过两个平面的法向量的夹角得到二面角的大小，但要注意结合实际图形判断所求角的大小．‎ ‎(2)找与棱垂直的方向向量法：分别在二面角的两个半平面内找到与棱垂直且以垂足为起点的两个向量，则这两个向量的夹角的大小就是二面角的大小．‎ ‎2．利用法向量求二面角时的两个注意点 ‎(1)对于某些平面的法向量要注意题中条件隐含着，不用单独求．‎ ‎(2)注意判断二面角的平面角是锐角还是钝角，可结合图形进行，以防结论错误.‎ 如图，△ABC和△BCD所在平面互相垂直，且AB＝BC＝BD＝2，∠ABC＝∠DBC＝120°，E，F分别为AC，DC的中点．‎ ‎(1)求证：EF⊥BC；‎ ‎(2)求二面角E－BF－C的正弦值．‎ ‎(1)证明：由题意，以B为坐标原点，在平面DBC内过B作垂直BC的直线为x轴，BC所在直线为y轴，在平面ABC内过B作垂直BC的直线为z轴，建立如图所示空间直角坐标系．‎ 易得B(0,0,0)，A(0，－1，)，D(，－1,0)，‎ C(0,2,0)．‎ 因而E，F.‎ 所以＝，＝(0,2,0)，‎ 因此·＝0.‎ 从而⊥，所以EF⊥BC.‎ ‎(2)解：平面BFC的一个法向量为n1＝(0,0,1)．‎ 设平面BEF的法向量n2＝(x，y，z)，‎ 又＝，＝，‎ 由得其中一个n2＝(1，－，1)．‎ 设二面角E－BF－C的大小为θ，且由题意知θ为锐角，‎ 则cos θ＝|cos〈n1，n2〉|＝＝，‎ 因此sin θ＝＝，‎ 即二面角E－BF－C的正弦值为.‎ ‎[方法技巧]　1.用向量来求空间角，只需将各类角转化成对应向量的夹角来计算，问题的关键在于确定对应线段的向量．‎ ‎2．合理建立空间直角坐标系 ‎(1)一般来说，如果已知的空间几何体中含有两两垂直且交于一点的三条直线时，就以这三条直线为坐标轴建立空间直角坐标系；如果不存在这样的三条直线，则应尽可能找两条垂直相交的直线，以其为两条坐标轴建立空间直角坐标系，即坐标系建立时以其中的垂直相交直线为基本出发点．‎ ‎(2)建系的基本思想是寻找其中的线线垂直关系，在没有现成的垂直关系时要通过其他已知条件得到垂直关系，在此基础上选择一个合理的位置建立空间直角坐标系．‎ ‎[易错防范]　1.利用向量求角，一定要注意将向量夹角转化为各空间角．‎ ‎2．求二面角要根据图形确定所求角是锐角还是钝角．‎ ‎ 真题演练集训 ‎ ‎1．[2016·新课标全国卷Ⅱ]如图，菱形ABCD的对角线AC与BD交于点O，AB＝5，AC＝6，点E，F分别在AD，CD上，AE＝CF＝，EF交BD于点H.将△DEF沿EF折到△D′EF的位置，OD′＝.‎ ‎(1)证明：D′H⊥平面ABCD；‎ ‎(2)求二面角B－D′A－C的正弦值．‎ ‎(1)证明：由已知，得AC⊥BD，AD＝CD.‎ 又由AE＝CF，得＝，故AC∥EF.‎ 因此EF⊥HD，从而EF⊥D′H.‎ 由AB＝5，AC＝6，得 DO＝BO＝＝4.‎ 由EF∥AC，得＝＝.‎ 所以OH＝1，D′H＝DH＝3.‎ 于是D′H2＋OH2＝32＋12＝10＝D′O2，故D′H⊥OH.‎ 又D′H⊥EF，而OH∩EF＝H，‎ 所以D′H⊥平面ABCD.‎ ‎(2)解：如图，以H为坐标原点，的方向为x轴正方向，的方向为y轴正方向，′的方向为z轴正方向，建立空间直角坐标系H－xyz.‎ 则H(0,0,0)，A(－3，－1,0)，B(0，－5,0)，‎ C(3，－1,0)，D′(0,0,3)，＝(3，－4,0)，‎ ＝(6,0,0)，＝(3,1,3)．‎ 设m＝(x1，y1，z1)是平面ABD′的法向量，‎ 则即 所以可取m＝(4,3，－5)．‎ 设n＝(x2，y2，z2)是平面ACD′的法向量，‎ 则即 所以可取n＝(0，－3,1)．‎ 于是cos〈m，n〉＝ ‎＝＝－，‎ sin〈m，n〉＝.‎ 因此二面角B－D′A－C的正弦值是.‎ ‎2．[2016·山东卷]在如图所示的圆台中，AC是下底面圆O的直径，EF是上底面圆O′的直径，FB是圆台的一条母线．‎ ‎(1)已知G，H分别为EC，FB的中点．求证：GH∥平面ABC；‎ ‎(2)已知EF＝FB＝AC＝2，AB＝BC，求二面角F－BC－A的余弦值．‎ ‎(1)证明：设FC的中点为I，连接GI，HI，‎ 在△CEF中，因为点G是CE的中点，‎ 所以GI∥EF.‎ 又EF∥OB，所以GI∥OB.‎ 在△CFB中，因为H是FB的中点，‎ 所以HI∥BC.‎ 又HI∩GI＝I，OB∩BC＝B，‎ 所以平面GHI∥平面ABC.‎ 因为GH⊂平面GHI，‎ 所以GH∥平面ABC.‎ ‎(2)解：解法一：连接OO′，则OO′⊥平面ABC.‎ 又AB＝BC，且AC是圆O的直径，‎ 所以BO⊥AC.‎ 以O为坐标原点，建立如图所示的空间直角坐标系O－xyz.‎ 由题意，得B(0,2，0)，C(－2，0,0)，‎ 所以＝(－2，－2，0)．‎ 过点F作FM垂直OB于点M，‎ 所以FM＝＝3，‎ 可得F(0，，3)．‎ 故＝(0，－，3)．‎ 设m＝(x，y，z)是平面BCF的法向量，‎ 由可得 可得平面BCF的一个法向量m＝.‎ 因为平面ABC的一个法向量n＝(0,0.1)，‎ 所以cos〈m，n〉＝＝.‎ 所以二面角F－BC－A的余弦值为.‎ 解法二：如图，连接OO′.过点F作FM垂直OB于点M，‎ 则有FM∥OO′.‎ 又OO′⊥平面ABC，‎ 所以FM⊥平面ABC.‎ 可得FM＝＝3.‎ 过点M作MN垂直BC于点N，连接FN.‎ 可得FN⊥BC，‎ 从而∠FNM为二面角F－BC －A的平面角．‎ 又AB＝BC，AC是圆O的直径，‎ 所以MN＝BMsin 45°＝，‎ 从而FN＝，可得cos ∠FNM＝.‎ 所以二面角F－BC－A的余弦值为.‎ ‎3．[2016·新课标全国卷Ⅲ]如图，四棱锥P－ABCD中，PA⊥底面ABCD，AD∥BC，AB＝AD＝AC＝3，PA＝BC＝4，M为线段AD上一点，AM＝2MD，N为PC的中点．‎ ‎(1)证明：MN∥平面PAB；‎ ‎(2)求直线AN与平面PMN所成角的正弦值．‎ ‎(1)证明：由已知，得AM＝AD＝2.‎ 如图，取BP的中点T，连接AT，TN.‎ 由N为PC的中点知，TN∥BC，TN＝BC＝2.‎ 又AD∥BC，故TN綊AM，四边形AMNT为平行四边形，于是MN∥AT.‎ 因为AT⊂平面PAB，MN⊄平面PAB，‎ 所以MN∥平面PAB.‎ ‎(2)解：取BC的中点E，连接AE.‎ 由AB＝AC，得AE⊥BC，‎ 从而AE⊥AD，‎ 且AE＝＝＝.‎ 以A为坐标原点，的方向为x轴正方向，建立如图所示的空间直角坐标系A－xyz.‎ 由题意知，‎ P(0,0,4)，M(0,2,0)，C(，2,0)，N，‎ ＝(0,2，－4)，＝，‎ ＝.‎ 设n＝(x，y，z)为平面PMN的法向量，‎ 则即 可取n＝(0,2,1)．‎ 于是|cos〈n，〉|＝＝，‎ 则直线AN与平面PMN所成角的正弦值为.‎ ‎4．[2015·新课标全国卷Ⅰ]如图，四边形ABCD为菱形，∠ABC＝120°，E，F是平面ABCD同一侧的两点，BE⊥平面ABCD，DF⊥平面ABCD，BE＝2DF，AE⊥EC.‎ ‎(1)证明：平面AEC⊥平面AFC；‎ ‎(2)求直线AE与直线CF所成角的余弦值．‎ ‎(1)证明：如图，连接BD，设BD∩AC＝G，连接EG，FG，EF.‎ 在菱形ABCD中，不妨设GB＝1.‎ 由∠ABC＝120°，可得AG＝GC＝.‎ 由BE⊥平面ABCD，AB＝BC可知，AE＝EC.‎ 又AE⊥EC，所以EG＝，且EG⊥AC.‎ 在Rt△EBG中，可得BE＝，故DF＝.‎ 在Rt△FDG中，可得FG＝.‎ 在直角梯形BDFE中，由BD＝2，BE＝，DF＝，可得EF＝.‎ 从而EG2＋FG2＝EF2，所以EG⊥FG.‎ 又AC∩FG＝G，所以EG⊥平面AFC.‎ 因为EG⊂平面AEC，‎ 所以平面AEC⊥平面AFC.‎ ‎(2)解：如图，以G为坐标原点，分别以，的方向为x轴，y轴正方向，||为单位长度，建立空间直角坐标系G－xyz.‎ 由(1)可得A(0，－，0)，E(1,0，)，‎ F，C(0，，0)，‎ 所以＝(1，，)，＝.‎ 故cos〈，〉＝＝－.‎ 所以直线AE与直线CF所成角的余弦值为.‎ ‎5．[2015·新课标全国卷Ⅱ]如图，长方体ABCD－A1B‎1C1D1中，AB＝16，BC＝10，AA1‎ ‎＝8，点E，F分别在A1B1，D‎1C1上，A1E＝D‎1F＝4.过点E，F的平面α与此长方体的面相交，交线围成一个正方形．‎ ‎(1)在图中画出这个正方形(不必说明画法和理由)；‎ ‎(2)求直线AF与平面α所成角的正弦值．‎ 解：(1)交线围成的正方形EHGF如图所示．‎ ‎(2)作EM⊥AB，垂足为M，‎ 则AM＝A1E＝4，EM＝AA1＝8.‎ 因为四边形EHGF为正方形，‎ 所以EH＝EF＝BC＝10.‎ 于是MH＝＝6，‎ 所以AH＝10.‎ 以D为坐标原点，的方向为x轴正方向，‎ 建立如图所示的空间直角坐标系D－xyz，‎ 则A(10,0,0)，H(10,10,0)，E(10，4,8)，F(0,4,8)，‎ ＝(10,0,0)，＝(0，－6,8)．‎ 设n＝(x，y，z)是平面α的法向量，‎ 则即 所以可取n＝(0,4,3)．‎ 又＝(－10,4,8)，‎ 故|cos〈n，〉|＝＝.‎ 所以AF与平面α所成角的正弦值为.‎ ‎ 课外拓展阅读 ‎ 巧用向量法求立体几何中的探索性问题 立体几何中的探索性问题立意新颖，形式多样，近年来在高考中频频出现，而空间向量在解决立体几何的探索性问题中扮演着举足轻重的角色，它是研究立体几何中的探索性问题的一个有力工具，应用空间向量这一工具，为分析和解决立体几何中的探索性问题提供了新的视角、新的方法．下面借“题”发挥，透视有关立体几何中的探索性问题的常见类型及其求解策略．‎ ‎1．条件追溯型 解决立体几何中的条件追溯型问题的基本策略是执果索因．其结论明确，需要求出使结论成立的充分条件，可将题设和结论都视为已知条件，即可迅速找到切入点．这类题目要求考生变换思维方向，有利于培养考生的逆向思维能力．‎ ‎[典例1]　 如图所示，在四棱锥S－ABCD中，SA⊥平面ABCD，底面ABCD为直角梯形，AD∥BC，∠BAD＝90°，且AB＝4，SA＝3.E，F分别为线段BC，SB上的一点(端点除外)，满足＝＝λ，当实数λ的值为________时，∠AFE为直角．‎ ‎[思路分析]　‎ ‎ ‎ ‎[解析]　因为SA⊥平面ABCD，∠BAD＝90°，‎ 故可建立如图所示的空间直角坐标系A－xyz.‎ 因为AB＝4，SA＝3，‎ 所以B(0,4,0)，S(0,0,3)．‎ 设BC＝m，则C(m,4,0)，‎ 因为＝＝λ，‎ 所以＝λ.‎ 所以－＝λ(－)．‎ 所以＝(＋λ)＝(0,4λ，3)．‎ 所以F.‎ 同理可得E，‎ 所以＝.‎ 因为＝，‎ 要使∠AFE为直角，即·＝0，‎ 则0·＋·＋·＝0，‎ 所以16λ＝9，‎ 解得λ＝.‎ ‎[答案]　 ‎2．存在判断型 以“平行、垂直、距离和角”为背景的存在判断型问题是近年来高考数学中创新型命题的一个重要类型，它以较高的新颖性、开放性、探索性和创造性深受命题者的青睐，此类问题的基本特征是：要判断在某些确定条件下的某一数学对象(数值、图形等)是否存在或某一结论是否成立．“是否存在”的问题的命题形式有两种情况：如果存在，找出一个来；如果不存在，需要说明理由．这类问题常用“肯定顺推”的方法．求解此类问题的难点在于涉及的点具有运动性和不确定性，所以用传统的方法解决起来难度较大，若用空间向量方法来处理，通过待定系数法求解其存在性问题，则思路简单、解法固定、操作方便．‎ ‎[典例2]　如图所示，四边形ABCD是边长为1的正方形，MD⊥平面ABCD，NB⊥平面ABCD，且MD＝NB＝1，E为BC的中点．‎ ‎(1)求异面直线NE与AM所成角的余弦值；‎ ‎(2)在线段AN上是否存在点S，使得ES⊥平面AMN？若存在，求线段AS的长；若不存在，请说明理由．‎ ‎[思路分析]　‎ ‎[解]　(1)如图所示，以D为坐标原点，建立空间直角坐标系D－xyz.‎ 依题意，得D(0,0,0)，A(1,0,0)，M(0,0,1)，‎ C(0,1,0)，B(1,1,0)，N(1,1,1)，E，‎ 所以＝，＝(－1,0,1)，‎ 因为|cos〈，〉|＝ ‎＝＝.‎ 所以异面直线NE与AM所成角的余弦值为.‎ ‎(2)假设在线段AN上存在点S，使得ES⊥平面AMN.‎ 连接AE，如图所示．‎ 因为＝(0,1,1)，可设＝λ＝(0，λ，λ)，‎ 又＝，‎ 所以＝＋＝.‎ 由ES⊥平面AMN，得 即解得λ＝，‎ 此时＝，||＝.‎ 经检验，当|AS|＝时，ES⊥平面AMN.‎ 故在线段AN上存在点S，使得ES⊥平面AMN，此时|AS|＝.‎ ‎3．结论探索型 立体几何中的结论探索型问题的基本特征是：给出一定的条件与设计方案，判断设计的方案是否符合条件要求．此类问题的难点是“阅读理解”和“整体设计”两个环节，因此，应做到审得仔细、找得有法、推得有理、证得有力，整合过程无可辩驳．‎ ‎[典例3]　某设计部门承接一产品包装盒的设计(如图所示)，客户除了要求AB，BE边的长分别为‎20 cm,‎30 cm外，还特别要求包装盒必须满足：①平面ADE⊥平面ADC；②平面ADE与平面ABC所成的二面角不小于60 °；③包装盒的体积尽可能大．若设计出的样品满足：∠ACB与∠ACD均为直角且AB长‎20 cm，矩形DCBE的边长BE＝‎30 cm，请你判断该包装盒的设计是否符合客户的要求，并说明理由．‎ ‎[思路分析]　‎ →→ ‎[解]　该包装盒的样品设计符合客户的要求．理由如下：‎ 因为四边形DCBE为矩形，∠ACB与∠ACD均为直角，‎ 所以以C为原点，分别以直线CA，CB，CD为x轴、y轴、z轴建立如图所示的空间直角坐标系C－xyz.‎ 因为BE＝‎30 cm，AB＝‎20 cm，‎ 设BC＝t cm，则AC＝ cm，‎ 则A(，0,0)，B(0，t,0)，D(0,0,30)，‎ E(0，t,30)，‎ 设平面ADE的法向量为n1＝(x，y，z)，‎ ＝(，0，－30)，＝(0，t,0)，‎ 因为n1·＝0且n1·＝0，‎ 所以 取x＝1，则n1＝.‎ 又平面ADC的一个法向量＝(0，t,0)，‎ 所以n1·＝1×0＋0×t＋×0＝0，‎ 所以n1⊥，‎ 所以平面ADE⊥平面ADC，所以满足条件①.‎ 因为平面ABC的一个法向量为n2＝(0,0,1)，‎ 设平面ADE与平面ABC所成二面角的平面角为θ，则cos θ≤，‎ 所以cos θ＝|cos〈n1，n2〉|＝≤，‎ 所以10≤t≤20，即当10≤t<20时，平面ADE与平面ABC所成的二面角不小于60°.‎ 由∠ACB与∠ACD均为直角知，‎ AC⊥平面DCBE，‎ 该包装盒可视为四棱锥A－BCDE，‎ 所以VA－BCDE＝S矩形BCDE·AC ‎＝·30t·＝10· ‎≤10＝2 000，‎ 当且仅当t2＝400－t2，即t＝‎10 cm时，VA－BCDE的体积最大，最大值为2 ‎000 cm3.‎ 而10