2019年高考理科数学考前30天--计算题专训（十四） 8页

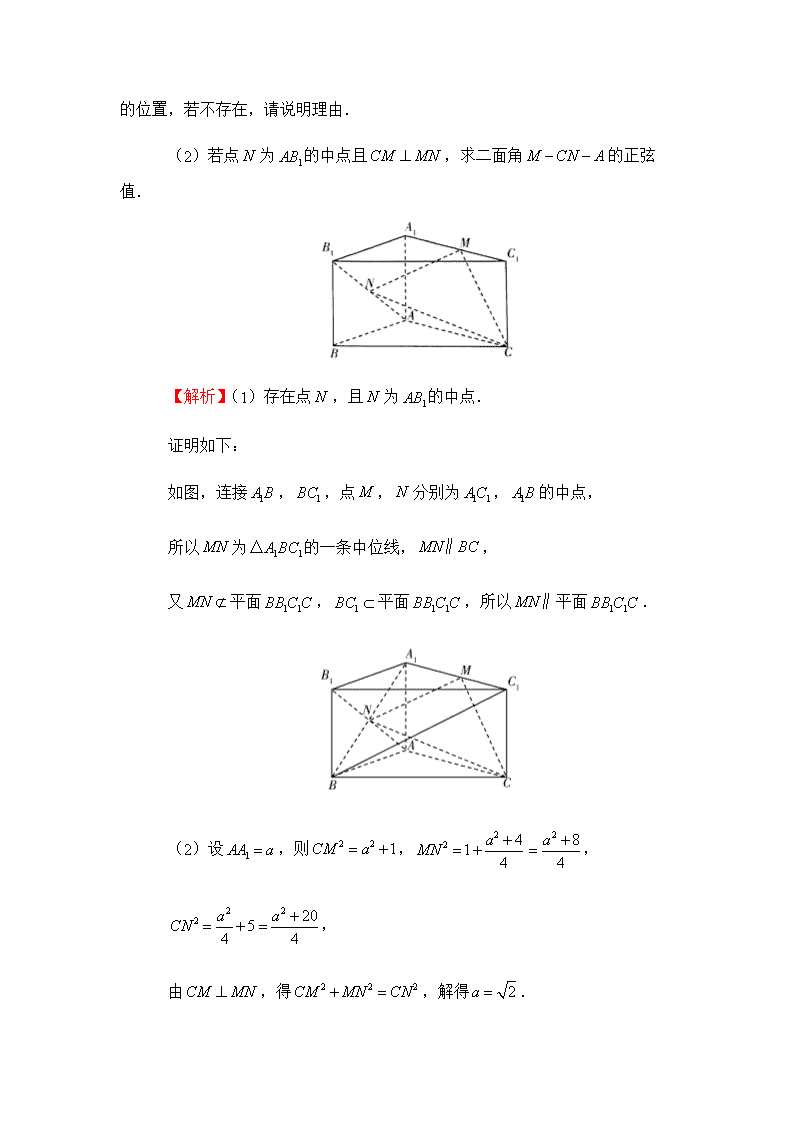
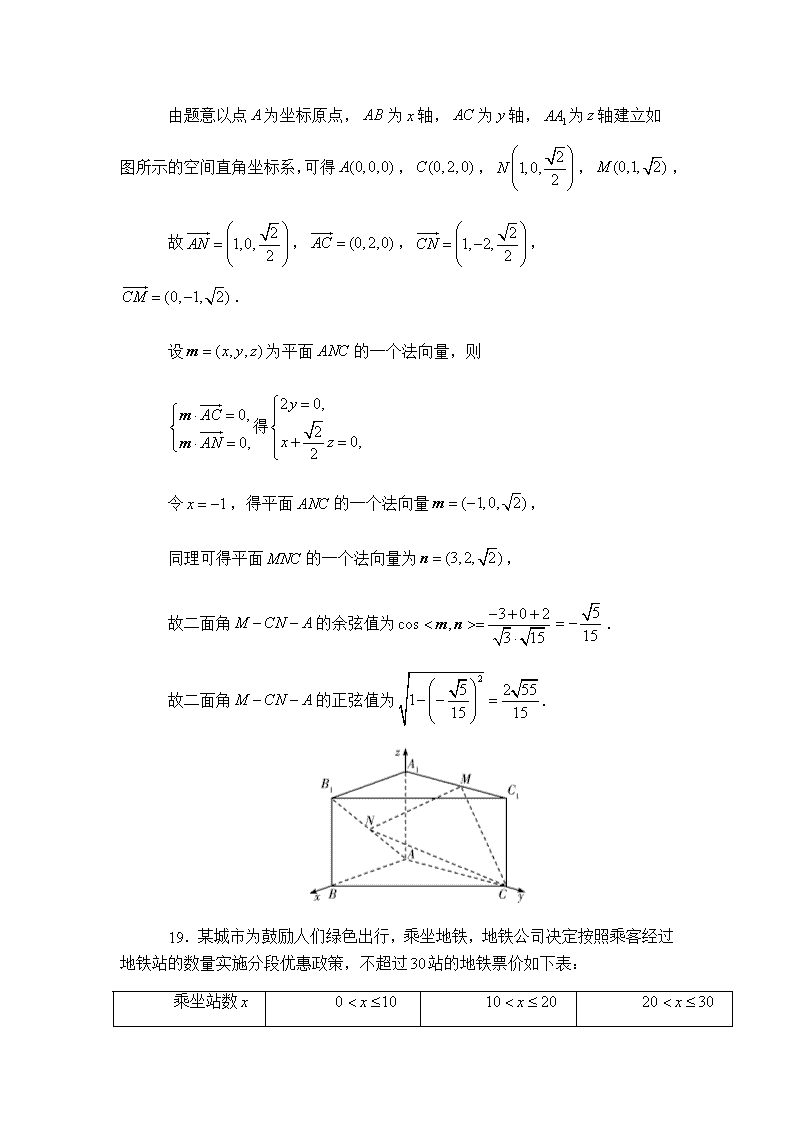
‎2019年高考理科数学考前30天--计算题专训（十四）‎ ‎17．已知在中，，，分别为内角，，的对边，且．‎ ‎（1）求角的大小；‎ ‎（2）若，，求的面积．‎ ‎【解析】（1）由及正弦定理得，‎ ‎，‎ 即，‎ 又，所以，‎ 又，所以．‎ ‎（2）由（1）知，又，易求得，‎ 在中，由正弦定理得，所以．‎ 所以的面积为．‎ ‎18．如图，在直三棱柱中，，，点为的中点，点为上一动点．‎ ‎（1）是否存在一点，使得线段平面？若存在，指出点 的位置，若不存在，请说明理由．‎ ‎（2）若点为的中点且，求二面角的正弦值．‎ ‎【解析】（1）存在点，且为的中点．‎ 证明如下：‎ 如图，连接，，点，分别为，的中点，‎ 所以为的一条中位线，，‎ 又平面，平面，所以平面．‎ ‎（2）设，则，，‎ ‎，‎ 由，得，解得．‎ 由题意以点为坐标原点，为轴，为轴，为轴建立如图所示的空间直角坐标系，可得，，，，‎ 故，，，．‎ 设为平面的一个法向量，则 得 令，得平面的一个法向量，‎ 同理可得平面的一个法向量为，‎ 故二面角的余弦值为．‎ 故二面角的正弦值为．‎ ‎19．某城市为鼓励人们绿色出行，乘坐地铁，地铁公司决定按照乘客经过地铁站的数量实施分段优惠政策，不超过站的地铁票价如下表：‎ 乘坐站数 票价（元）‎ 现有甲、乙两位乘客同时从起点乘坐同一辆地铁，已知他们乘坐地铁都不超过站．甲、乙乘坐不超过站的概率分别为，；甲、乙乘坐超过站的概率分别为，．‎ ‎（1）求甲、乙两人付费相同的概率；‎ ‎（2）设甲、乙两人所付费用之和为随机变量，求的分布列和数学期望．‎ ‎【解析】（1）由题意知甲乘坐超过站且不超过站的概率为，‎ 乙乘坐超过站且不超过站的概率为，‎ 设“甲、乙两人付费相同”为事件，则，‎ 所以甲、乙两人付费相同的概率是．‎ ‎（2）由题意可知的所有可能取值为：，，，，．‎ ‎，‎ ‎，‎ ‎，‎ ‎，‎ ‎．‎ 因此的分布列如下：‎ 所以的数学期望．‎ ‎20．在平面直角坐标系中，已知椭圆的离心率为，，分别为椭圆的上顶点和右焦点，的面积为，直线与椭圆交于另一个点，线段的中点为．‎ ‎（1）求直线的斜率；‎ ‎（2）设平行于的直线与椭圆交于不同的两点，，且与直线交于点，求证：存在常数，使得．‎ ‎【解析】（1）因为椭圆的离心率为，所以，即，，‎ 所以，，所以，所以，所以椭圆的方程为．‎ 直线的方程为，联立消去得，所以或，‎ 所以，从而得线段的中点．‎ 所以直线的斜率为．‎ ‎（2）由（1）知，直线的方程为，直线的斜率为，设直线的方程为．‎ 联立得所以点Q的坐标为．‎ 所以，．‎ 所以．‎ 联立消去得，‎ 由已知得，又，得．‎ 设，，则，，‎ ‎，．‎ 所以，‎ ‎，‎ 故．‎ 所以．所以存在常数，使得．‎ ‎21．已知函数，．‎ ‎（1）求函数的单调区间；‎ ‎（2）证明：．‎ ‎【解析】（1）由题易知，‎ 当时，，当时，，‎ 所以的单调递减区间为，单调递增区间为．‎ ‎（2）的定义域为，要证，即证．‎ 由（1）可知在上递减，在上递增，所以．‎ 设，，因为，‎ 当时，，当时，，‎ 所以在上单调递增，在上单调递减，所以，‎ 而，所以．‎