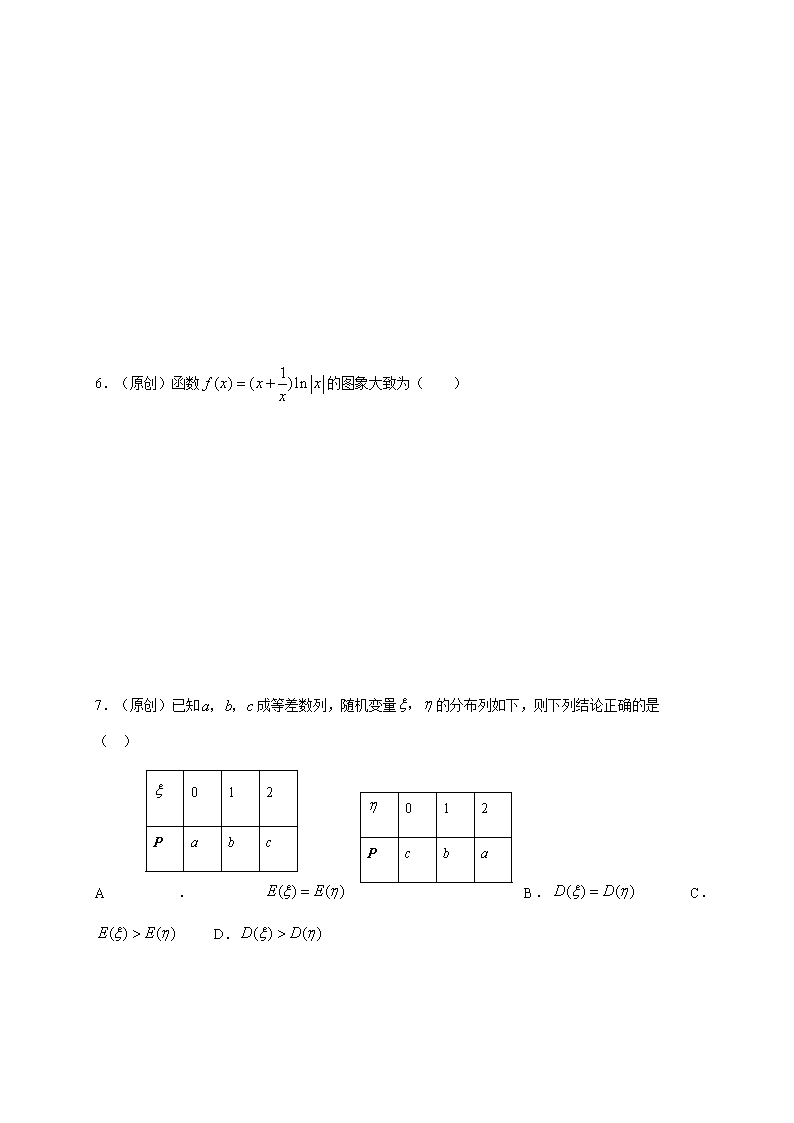浙江省宁波市鄞州中学2020届高三高考冲刺考试数学试题 18页

‎2020浙江高考数学冲刺卷 本试卷分第（Ⅰ）卷（选择题）和第（Ⅱ）卷（非选择题）两部分．满分150分，考试时间120分钟 第（Ⅰ）卷（选择题 共40分）‎ 一、选择题：本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．（原创）设全集，集合，集合，则（ ）‎ A．4 B．2，3，6 C．2，3，7 D．2，3，4，7‎ ‎2．（原创）若双曲线的两条渐近线方程为，则双曲线的离心率是（ ）‎ A． B． C． D．或 ‎3．（原创）实数满足，则的取值范围是（ ）‎ A． B． C． D．‎ ‎4．（原创）设，则“”是“”的（ ）‎ A．充分不必要条件 B．充要条件 C．必要不充分条件 D．既不充分又不必要条件 ‎5．（原创）冶铁技术在我国已有悠久的历史，据史料记载，我国最早的冶铁技术可以追溯到春秋晚期，已知某铁块的三视图如图所示，若将该铁块浇铸成一个铁球，则铁球的半径是（ ）‎ A． B． C． D．‎ ‎6．（原创）函数的图象大致为（ ）‎ D ‎7．（原创）已知成等差数列，随机变量的分布列如下，则下列结论正确的是（ ）‎ ‎0‎ ‎1‎ ‎2‎ P a b c ‎0‎ ‎1‎ ‎2‎ P c b a A． B． C． D．‎ ‎8．（改编）已知函数，若关于的方程恰有4个不相等的实数根，则实数的取值范围是（ ）‎ A． B． C． D．‎ ‎9．（原创）如图，点是矩形的边上一点，将沿直线折起至，点在平面上的投影为，平面与平面所成锐二面角为，直线与平面所成角为，若，则下列说法正确的是（ ）‎ A． B． C． D．无法确定 ‎ ‎10．（改编）数列满足，下列说法正确的是（ ）‎ A．存在正整数，使得 B．存在正整数，使得 ‎ C．对任意正整数，都有 D．数列单调递增 ‎ 第（Ⅱ）卷（非选择题 共110分）‎ 二、填空题：本大题7小题，多空题每题6分，单空每题4分，共36分，把答案填在题中的横线上．‎ ‎11．（原创）复数满足，则_____；_____‎ ‎12．（原创）点是圆上的动点，点满足（‎ 为坐标原点），则点的轨迹方程是_______________；若点又在直线上，则的最小值 是________‎ ‎13．（原创）已知在的展开式中，只有第四项的二项式系数最大，则_____；项的系数为______‎ ‎14．（原创）四边形内接于圆，其中为直径，若，则_______；四边形的面积是_______‎ ‎15．（原创）函数且，若，且， 则_______‎ ‎16．（改编）过点的直线与抛物线相交于两点，为轴上一点，若为等边三角形，则_______‎ ‎17．（原创）中，依次为的三等分点，若，则的最小值是__ _‎ 三、解答题：本大题共5小题，共74分．解答题应写出必要的文字说明、证明过程或演算步骤．‎ ‎18．（本题14分）（原创）已知函数 ‎（1）已知，函数为奇函数，求值；‎ ‎（2）求函数的值域. ‎ ‎19．（本题15分）（改编）如图，菱形与正的边长均为，且平面平面，平面，且 ‎（1）求证：平面 ‎（2）若，求二面角的余弦值.‎ ‎20．（本题15分）（改编）正项数列的前项和为，满足对每个，成等差数列，且成等比数列.‎ ‎（1）求的值；（2）求的通项公式；（3）求证：‎ ‎21．（本题15分）（改编）椭圆的左、右焦点分别为，点在椭圆上，直线与椭圆的另一个交点分别为.‎ ‎（1）若点坐标为，且，求椭圆的方程；‎ ‎（2）设，，求证：为定值.‎ ‎22．（本题15分）（改编）已知函数 ‎（1）若曲线在点处的切线与直线平行，求实数的值；‎ ‎（2）若在上恒成立，求的最小值. ‎ 数学试卷参考答案与解题提示 一、选择题：本大题共10小题，每小题4分，共40分．‎ ‎1.【答案】B ‎【考查目标】本题考查集合的交、补运算，属于基础题.‎ ‎【试题解析】，，故选择B ‎2. 【答案】D ‎【考查目标】本题考查双曲线的几何性质，考查双曲线的渐近线、离心率的概念，考查考生基本运算求解能力，属于基础题.‎ ‎【试题解析】易得双曲线方程为，当时离心率，当时离心率，故选择D ‎3. 【答案】A ‎【考查目标】本题考查简单的线性规划问题，考查考生的作图能力和直观想象能力，属于基础题.‎ ‎【试题解析】作图即得平面区域，由几何意义截距可知 ‎4. 【答案】A ‎【考查目标】本题考查简易逻辑中的充分条件与必要条件，求解时要转化成集合间的关系进行判断，考查考生等价转化思想，属于稍难题.‎ ‎【试题解析】易得，，故选A ‎5. 【答案】D ‎【考查目标】本题考查三视图和直观图的关系，考查考生空间想象能力，四面体、球体的体积的计算和空间图形的识别能力，属于稍难题.‎ ‎【试题解析】由三视图可得四面体，设球半径为，则，故选择D ‎6. 【答案】C ‎【考查目标】本题考查函数的图像和性质，考查考生分析函数性质能力和图像识别能力，属于稍难题.‎ ‎【试题解析】，函数为奇函数，当时，故选择C ‎7. 【答案】B ‎【考查目标】本题考查离散型随机变量的分布列、数学期望及方差，考查考生运算求解能力，属于稍难题.‎ ‎【试题解析】，‎ ‎，，，，故选择B ‎8. 【答案】D ‎【考查目标】本题考查函数与方程，考查考生用导数研究三次函数的图像和性质，导数的几何意义，函数的零点等知识，考查考生用数形结合方法解决问题的能力，属于稍难题.‎ ‎【试题解析】设，则易得当时，单调递减，当时，单调递增，数形结合可知，‎ 直线与在处有一个交点，在处有一个交点，故在处需2个交点，直线经过点时，当直线与相切于时，故选择D ‎9. 【答案】A ‎【考查目标】本题考查空间直线与平面的位置关系、直线与平面所成角，二面角等立体几何知，考查考生空间想象能力和作图能力，属于难题.‎ ‎【试题解析】易得当时，‎ 设交于，则，‎ 又由于，‎ 故选择A ‎10. 【答案】C ‎【考查目标】本题考查数列的递推关系、数列的通项、数列的求和、数列与不等式的综合问题，考查考生的逻辑思维能力，及分析问题、解决问题的能力，属于难题.‎ ‎【试题解析】，‎ ‎，，故选择C 二、填空题：本大题7小题，多空题每题6分，单空每题4分，共36分．‎ ‎11.【答案】；‎ ‎【考查目标】本题考查复数的四则运算，考查考生基本运算求解能力，属于基础题.‎ ‎【试题解析】‎ ‎12.【答案】；‎ ‎【考查目标】本题考查直线与圆的位置关系，动点轨迹方程的求法，直线的倾斜角与斜率，考查考生用数形结合方法解决问题的能力，属于基础题.‎ ‎【试题解析】设，则代入方程得；‎ 数形结合，直线与圆相切时取得最小值 ‎13.【答案】； ‎ ‎【考查目标】本题考查二项式定理展开式的通项，考查基本运算求解能力，属于基础题.‎ ‎【试题解析】由二项式系数的对称性质得，由通项公式 令，故得含的项系数为 ‎14.【答案】；‎ ‎【考查目标】本题考查三角形中的边角关系、三角形面积公式、倍角公式的应用，考查考生三角恒等变形能力、图形识别能力、方程思想，属于稍难题.‎ ‎【试题解析】连接得 由面积公式的面积为 ‎15.【答案】‎ ‎【考查目标】本题考查对数的运算法则、对数函数的图像和性质，考查考生观察能力、运算求解能力、画图能力，属于稍难题.‎ ‎【试题解析】根据函数图象性质得函数的图象关于直线对称，则易得 ‎ 又 同理可得，则 ‎16.【答案】‎ ‎【考查目标】本题考查直线与抛物线的位置关系，考查考生运算求解能力，属于稍难题 ‎【试题解析】由题意可知，直线的斜率存在且不为0，‎ 故设直线方程为：代入抛物线方程得①‎ 设，②‎ ‎，则中点坐标为 中垂线方程为，令得，则 为正三角形，到直线的距离，‎ 代入②满足，则 ‎17.【答案】‎ ‎【考查目标】‎ 本题考查向量的运算、平面向量的基本定理，考查考生综合运用向量、三角、不等式等知识解决问题的能力，属于难题.‎ ‎【试题解析】，设 三、解答题：本大题共5小题，共74分．‎ ‎18. 【答案】（1）或；（2）‎ ‎【考查目标】本题考查三角函数的图像和性质、函数的奇偶性，考查考生三角函数的恒等变形能力，属于基础题.‎ ‎【试题解析】‎ ‎（1）奇恒成立——————2分 恒成立————4分 ‎，又，所以或.————————6分 ‎（2）——8分 ‎——————10分 ‎————————12分 因为，所以，‎ 所以函数的值域是.————————14分 ‎19. 【答案】（1）见解析；（2）‎ ‎【考查目标】本题考查线面平行、线面垂直、面面垂直的性质定理和判定定理、用向量工具求二面角的方法，考查考生空间想象能力和运算求解能力，属于基础题.‎ ‎【试题解析】‎ ‎（1）如图，作于，连，————1分 平面平面，平面，‎ 且————3分 又平面，且，‎ ‎，且，四边形是平行四边形，————5分，‎ ‎——————7分 ‎（2），——————8分 以为原点，所在直线为轴建立空 间直角坐标系，如图所示.————9分 则 有————10分 设平面的一个法向量为，‎ 由，令，取，————11分 设平面的一个法向量为，‎ 由，令，取，————12分 则，——————14分 由题意知二面角是钝二面角，故二面角的余弦值是.——15分 ‎20.【答案】（1）；（2）；（3）见解析 ‎【考查目标】本题考查等差数列、等比数列的通项公式、前项和公式，递推数列求通项的方法，考查考生运用所学的数学方法：数学归纳法，比较法、放缩法解决问题的能力，属于稍难题.‎ ‎【试题解析】‎ ‎（1）————————2分 ‎————3分 因为，所以————4分 ‎（2）‎ 当时，————6分 又符合上式，所以————7分 是首项为，公比为的等比数列 ‎————10分 ‎（3）因为，当时，‎ ‎————13分 易知时，原不等式成立；当时：‎ 综上，原不等式成立————15分 ‎21. 【答案】（1）；（2）‎ ‎【考查目标】本题考查椭圆的标准方程、几何性质、直线与椭圆的位置关系，考查考生函数与方程思想、数形结合思想，逻辑推理能力和运算求解能力.‎ ‎【试题解析】‎ ‎（1），所以椭圆方程为——————4分 ‎（2）法一：坐标法 设，‎ 当时，——————5分 当时，，，——————7分 其中：，从而————9分 由——————11分 同理，从而——————13分 ‎——————15分 法二：三角法 不妨设点在轴上方，由余弦定理易得：‎ ‎，‎ ‎，——————8分 所以，‎ ‎——————10分 又 ‎————13分 所以 ‎————15分 ‎22. 【答案】（1）；（2）‎ ‎【考查目标】本题考查利用导数的几何意义求切线方程、讨论函数的单调性、证明不等式，考查考生函数与方程思想、分类讨论思想、数形结合思想的综合运用，考查逻辑推理能力和运算求解能力，证明不等式的关键是先将问题进行等价转化，再构造函数利用导数研究新函数的性质.‎ ‎【试题解析】‎ ‎（1）————2分，‎ 由题意知————4分 ‎（2）‎ ‎ ————7分 设，则原不等式——————9分 由，易知时，，时，，‎ 所以在上单调减，在上单调增——————11分 因为是求的最小值，故设，又，所以————12分 所以，原不等式恒成立 ‎————13分 设，则，易知时，，时，，‎ 所以在上单调增，在上单调减———14分 所以——————15分