- 672.50 KB
- 2021-04-14 发布
第17天 测量距离问题
高考频度:★★☆☆☆ 难易程度:★★☆☆☆
典例在线
如图,在高速公路建设中需要确定隧道的长度,工程技术人员已测得隧道两端的两点A,B到点C的距离AC=BC=1 km,且C=120°,则A,B两点间的距离为
A. B.
C. D.
【参考答案】A
【解题必备】当的长度不可直接测量时,求,之间的距离有以下三种类型.
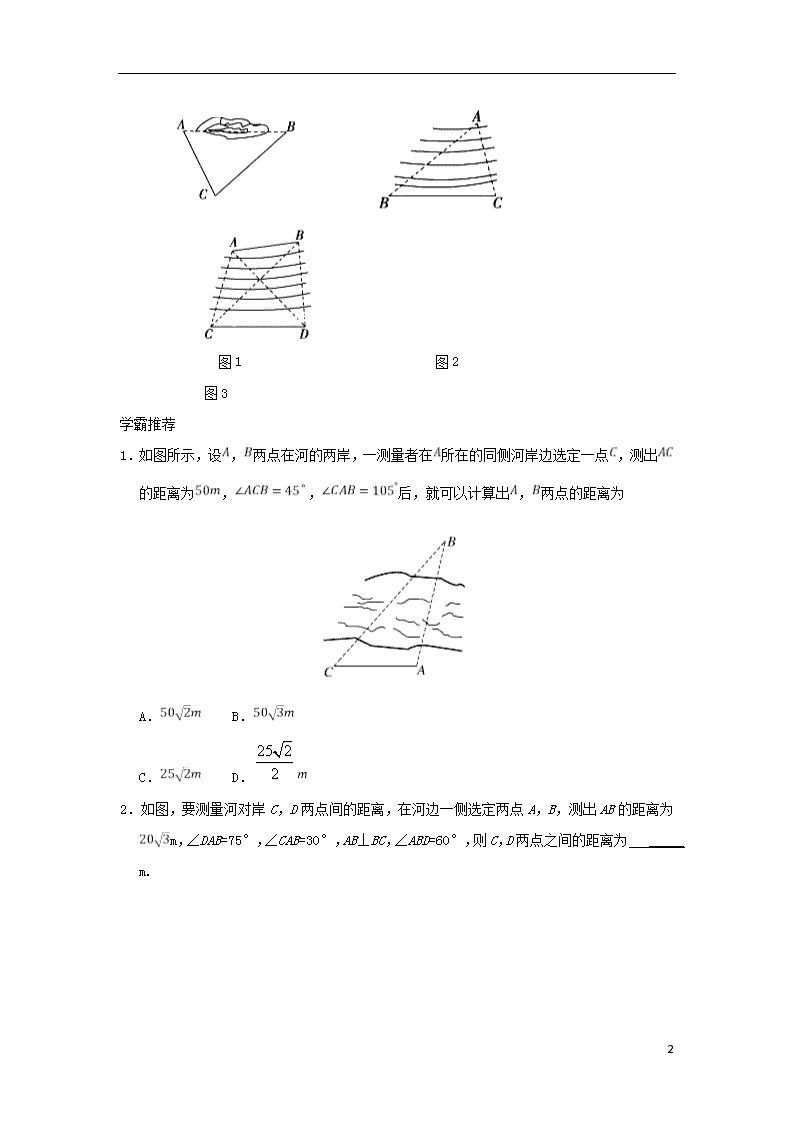
(1)如图1,A,B之间不可达也不可视,计算方法:测量,及角,由余弦定理可得.
(2)如图2,B,C与点A可视但不可达,计算方法:测量,角,角,则,由正弦定理可得.
(3)如图3,C,D与点A,B均可视不可达,计算方法:测量
在中由正弦定理求,在中由正弦定理求,在中由余弦定理求.
4
图1 图2 图3
学霸推荐
1.如图所示,设,两点在河的两岸,一测量者在所在的同侧河岸边选定一点,测出的距离为,,后,就可以计算出,两点的距离为
A. B.
C. D.
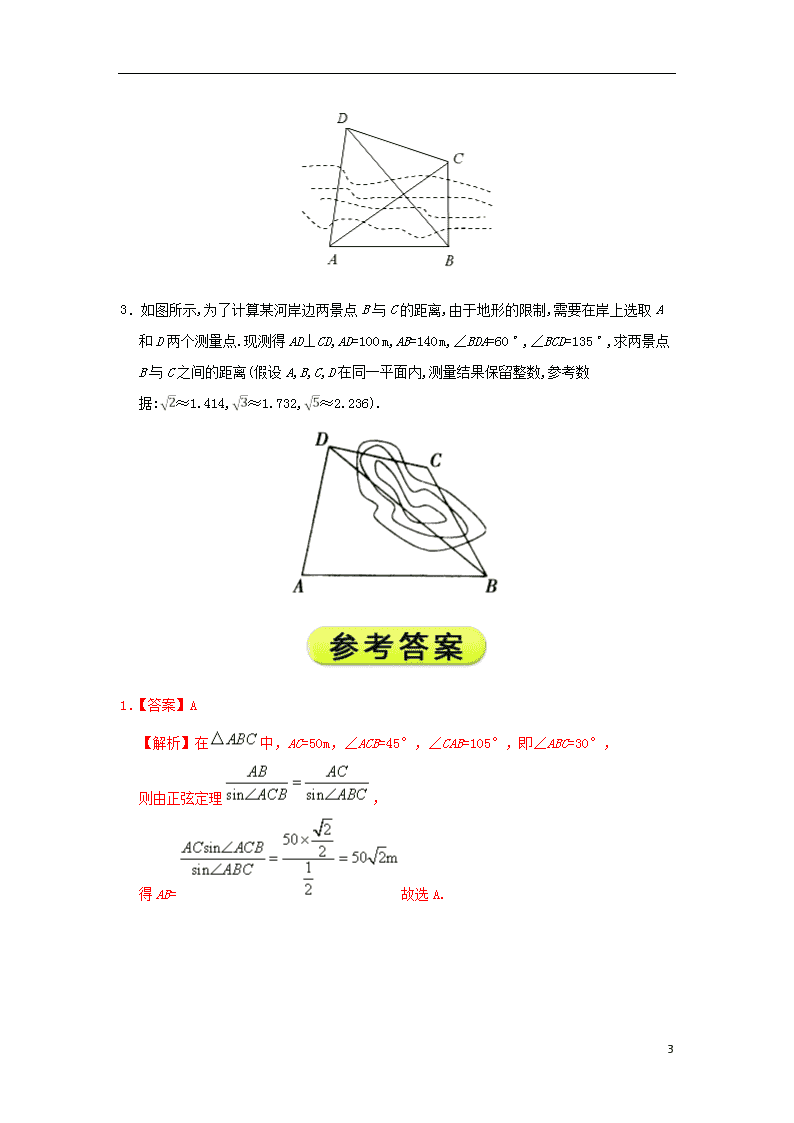
2.如图,要测量河对岸C,D两点间的距离,在河边一侧选定两点A,B,测出AB的距离为m,∠DAB=75°,∠CAB=30°,AB⊥BC,∠ABD=60°,则C,D两点之间的距离为 _____ m.
4
3.如图所示,为了计算某河岸边两景点B与C的距离,由于地形的限制,需要在岸上选取A和D两个测量点.现测得AD⊥CD,AD=100 m,AB=140 m,∠BDA=60°,∠BCD=135°,求两景点B与C之间的距离(假设A,B,C,D在同一平面内,测量结果保留整数,参考数据:≈1.414,≈1.732,≈2.236).
1.【答案】A
【解析】在中,AC=50m,∠ACB=45°,∠CAB=105°,即∠ABC=30°,
则由正弦定理,
得AB=故选A.
4
3.【解析】在中,设BD为x,则BA2=BD2+AD2-2BD·AD·cos ∠BDA,
即1402=x2+1002-2×100×x×cos 60°,整理,得x2-100x-9600=0,
解得x1=160,x2=-60(舍去),故BD=160(m).
在中,由正弦定理,得,
又AD⊥CD,∠BDA=60°,所以∠CDB=30°,
所以BC·sin 30°=80≈113(m).
即两景点B与C之间的距离约为113 m.
4
相关文档
- 化学卷·2018届江苏省扬州市宝应县2021-04-14 13:10:3327页
- 高中数学人教a版选修2-2(课时训练):1.2021-04-14 13:09:3711页
- 高中学生毕业档案自我鉴定20202021-04-14 13:09:126页
- 2020版新教材高中化学第2章化学键2021-04-14 13:08:5736页
- 2020新教材高中化学第2章化学键化2021-04-14 13:08:3810页
- 上海教育高中数学三上计数原理II加2021-04-14 13:07:524页
- 2020版高中物理 第四章 牛顿运动定2021-04-14 13:07:485页
- 2020高中数学 专题强化训练1 导数2021-04-14 13:07:485页
- 2017-2018学年高中政治必修一课时2021-04-14 13:06:466页
- 2019-2020学年广西壮族自治区田阳2021-04-14 13:06:279页