- 460.50 KB
- 2021-04-14 发布
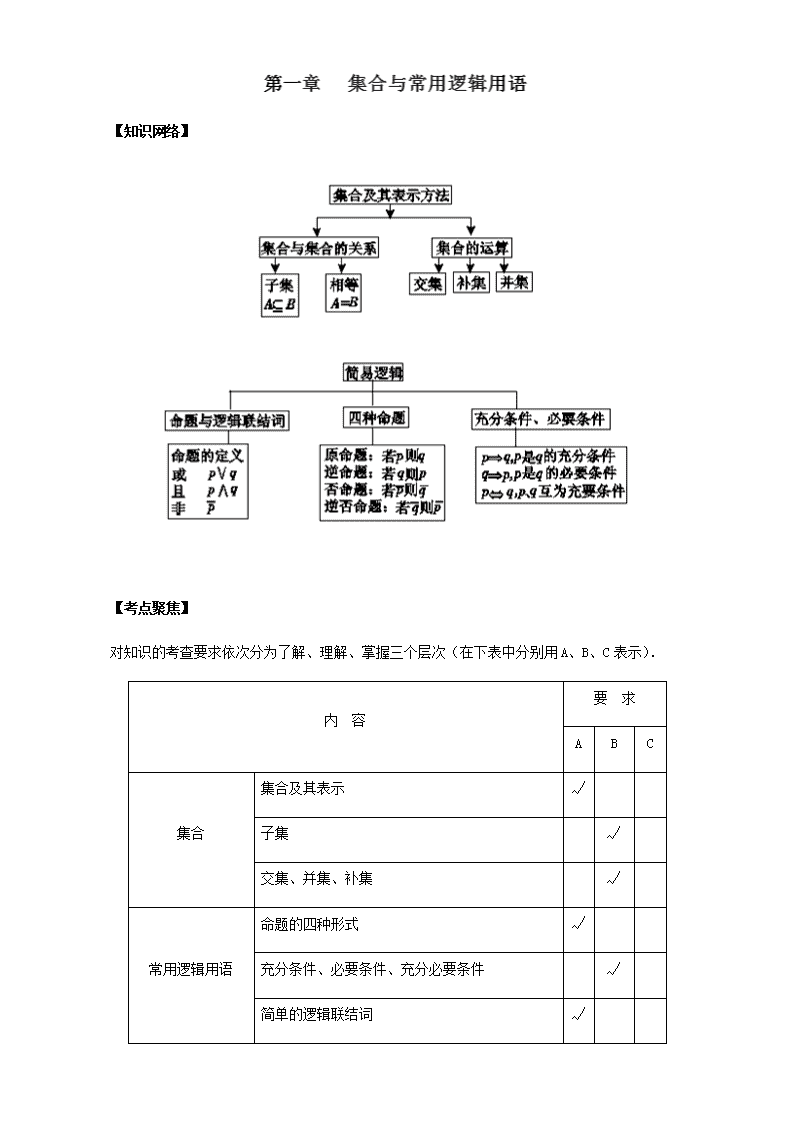
【知识网络】
【考点聚焦】
对知识的考查要求依次分为了解、理解、掌握三个层次(在下表中分别用A、B、C表示).
内 容
要 求
A
B
C
集合
集合及其表示
√
子集
√
交集、并集、补集
√
常用逻辑用语
命题的四种形式
√
充分条件、必要条件、充分必要条件
√
简单的逻辑联结词
√
全称量词与存在量词
√
一、集合及其表示
1.【原题】(必修1第7页练习第三题(3))判断下列两个集合之间的关系:
【原题解读】
(1)知识上;需要熟悉集合的表达方式,明确集合间关系(子集,真子集,相等)的概念。
(2)思路方法上;需要能对无限集合的关系进行判断,可采用列举法或数学表达的转换和
统一来确定集合间的关系。体现的数学思想有对应思想及数学符号表达能力。
变式【2015新课标高考】已知集合,集合,则( )
A. B.
C. D.
【答案】D.
【解析】由题可得;,,故选D.
二、集合的运算
1.【原题】(必修1第十二页习题1.1B组第1题)已知集合A={1,2},集合B满足A∪B={1,2},则这样的集合B有 个.
【解析】∵A={1,2},又A∪B={1,2},∵,则B集合可以是:,{1},{2},{1,2};有4个;
【原题解读】本题需要注意,则问题可化为求集合A的子集个数问题,即为。
变式1【2016北京模拟】已知,若非空集合A满足,对任意都有,则这样的集合有 个。
【答案】7
【解析】符合条件的集合A有,共7个
变式2 已知集合有个元素,则集合的子集个数有 个,真子集个数有 个.
【答案】;.
变式3 满足条件的所有集合的个数是 个.
【答案】4.
【解析】3必须在集合里面,的个数相当于2元素集合的子集个数,故有4个.
2.【原题】(必修1第四十四页复习参考题A组第4题)已知集合,集合,若,求实数的值.
【原题解读】本题给出集合为两个方程的根,而条件,可对集合B的情况进行分类,从而求出的值;体现了分类思想和对集合语言的深刻理解和运用。
注意;空集是一个特殊的集合,它不含任何元素,是任何集合的子集,是任何非空集合的真子集,在解决集合之间关系问题时,它往往易被忽视而引起解题失误。
变式【2016邯郸模拟】已知集合,集合B=若,求实数p的取值范围。
【答案】
【解析】由(1)B=时,即p+12p-1,故p2;
(2)B时,,又,
则;借助数轴表示知,
故。由(1)(2)得。
3. 原题(必修1第十二页习题1.1 A组第10题)已知集合,,求,,,
变式1 已知全集且则等于( ) A. B. C. D.
【答案】C.
【解析】集合,所以,集合,所以为,故选C .
变式2 设集合,,则等于( )
A. B. C. D.
【答案】B.
【解析】,,所以,故选B .
变式3 已知集合集合则等于 ( )
A. B. C. D.
【答案】D.
【解析】集合,故选D .
【感受高考】
1. 【2016新课标1理】设集合 ,,则 ( )
(A) (B) (C) (D)
【答案】D
【解析】
2.【2016高考新课标2理数】已知集合,,则( )
(A) (B) (C) (D)
【答案】C
【解析】
试题分析:集合,而,
所以,故选C.
3. 【2016高考新课标Ⅲ文数】设集合,则=( )
(A) (B) (C) (D)
【答案】C
【解析】
试题分析:由补集的概念,得,故选C.
4.【2016高考新课标1文数】设集合,,则( )
(A){1,3} (B){3,5} (C){5,7} (D){1,7}
【答案】B
【解析】
试题分析:集合与集合公共元素有3,5,,故选B.
5.【2016高考山东理数】设集合 则=( )
(A) (B) (C) (D)
【答案】C
【解析】
试题分析:,,则,选C.
6.【2016高考山东理数】已知直线a,b分别在两个不同的平面α,β内.则“直线a和直线b相交”是“平面α和平面β相交”的( )
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
【答案】A
【解析】
7. 【2016高考浙江理数】命题“,使得”的否定形式是( )
A.,使得 B.,使得
C.,使得 D.,使得
【答案】D
【解析】
试题分析:的否定是,的否定是,的否定是.故选D.
8.【2016高考天津理数】设{}是首项为正数的等比数列,公比为q,则“q<0”是“对任意的正整数n,”的( )
A 充要条件 B 充分而不必要条件
C 必要而不充分条件 D 既不充分也不必要条件
【答案】C
【解析】