- 1019.00 KB
- 2021-04-14 发布
2019-2020 学年宁夏石嘴山市平罗中学高二(上)期末数学试
卷(文科)
一、选择题(本大题共 12 小题)
1.一个田径队,有男运动员 56 人,女运动员 42 人,比赛后,立即用分层抽样的方法,从全体
队员中抽出一个容量为 28 的样本进行尿样兴奋剂检查,其中男运动员应抽的人数为( )
A. 16 B. 14 C. 28 D. 12
【答案】A
【解析】
因为每个个体被抽到的概率等于 ,根据分层抽样方法的原理可得样本中男运动员
的人数为 ,故选 A.
2.原点到直线 的距离是( )
A. B. C. D.
【答案】B
【解析】
【分析】
利用点到直线距离公式直接求解即可.
【详解】由点到直线距离公式得:
故选:
【点睛】本题考查点到直线距离的求解问题,考查基础公式的应用.
3.已知命题 R, ,则
A. R, B. R,
C. R, D. R,
【答案】C
【解析】
试题分析:因为全称命题的否定是特称命题,特称命题的否定是全称命题,所以,只需将原命
28 2
56 42 7
=+
256 167
× =
3 4 26 0x y+ − =
26 7
7
26
5
24
5
27
5
26 26
59 16
d
−= =
+
B
:p x∀ ∈ sin 1x
:p x¬ ∃ ∈ sin 1x :p x¬ ∀ ∈ sin 1x
:p x¬ ∃ ∈ sin 1x > :p x¬ ∀ ∈ sin 1x >
题中的条件全称改特称,并对结论进行否定,故答案为 .
考点:全称命题与特称命题的否定.
4.“ ”是“ ”的 ( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
【答案】A
【解析】
主要考查充要条件的概念及充要条件的判定方法.
解:对于“x>0”⇒“x≠0”,反之不一定成立.因此“x>0”是“x≠0”的充分而不必要条件.故选 A.
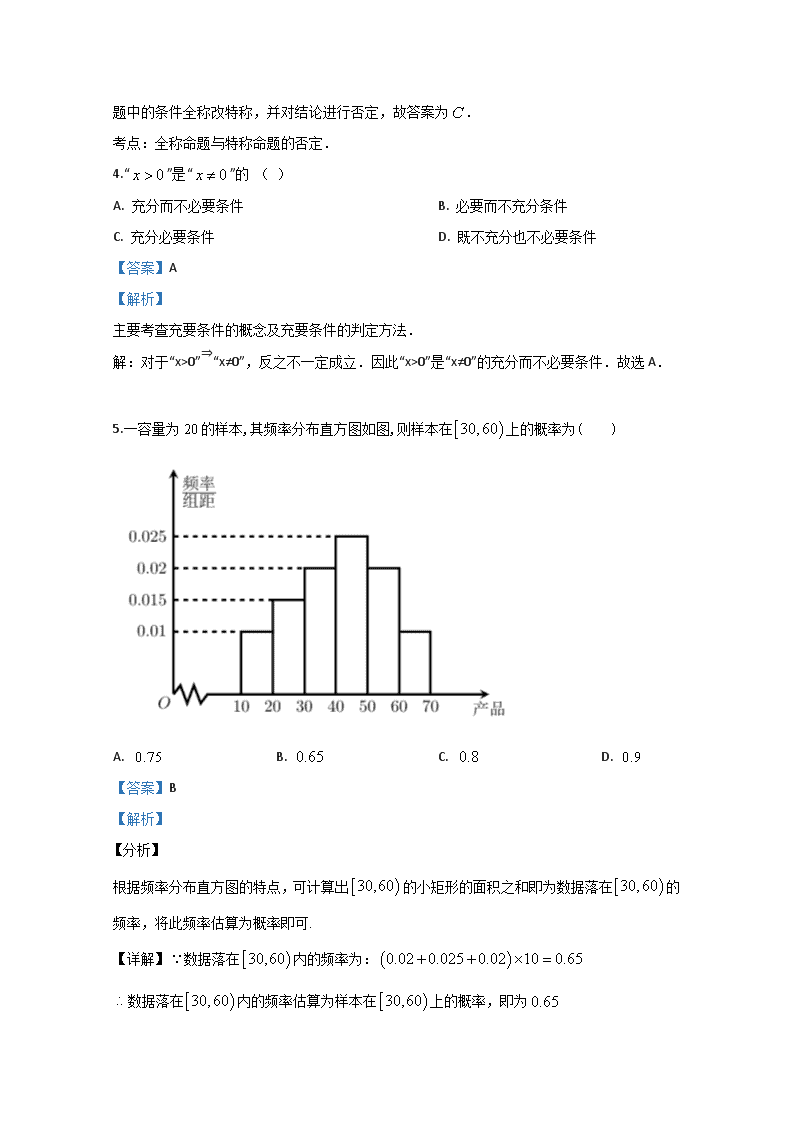
5.一容量为 20 的样本,其频率分布直方图如图,则样本在 上的概率为( )
A. B. C. D.
【答案】B
【解析】
分析】
根据频率分布直方图的特点,可计算出 的小矩形的面积之和即为数据落在 的
频率,将此频率估算为概率即可.
【详解】 数据落在 内的频率为:
数据落在 内的频率估算为样本在 上的概率,即为
【
C
0x > 0x ≠
[ )30,60
0.75 0.65 0.8 0.9
[ )30,60 [ )30,60
[ )30,60 ( )0.02 0.025 0.02 10 0.65+ + × =
∴ [ )30,60 [ )30,60 0.65
故选:
【点睛】本题考查利用频率分布直方图计算频率的问题,属于基础题.
6.已知 : , : ,则下列判断错误的是( )
A. “ 或 ”为真,“非 ”为假
B. “ 且 ”为假,“非 ”为真
C. “ 且 ”为假,“非 ”为假
D. “ 或 ”为真,“非 ”为真
【答案】C
【解析】
【分析】
命题 p 是假命题,q 是真命题,根据复合命题真值表可判断真假.
【详解】因为命题 p 假命题,q 是真命题,
所以“ 且 ”为假,“ 或 ”为真,“非 ”为真,“非 ”为假,故选 C.
【点睛】本题主要考查了含逻辑联结词“或”、“且”、“非”的命题真假的判断,属于中档
题.
7.以点 P(2,-3)为圆心,并且与 y 轴相切的圆的方程是( )
A. B.
C. D.
【答案】C
【解析】
【分析】
因为与 y 轴相切,所以可知圆的半径 ,根据圆心坐标,可得圆的标准方程.
【详解】圆心为(2,-3)并且与 y 轴相切
所以半径
所以圆的方程为(x-2)2+(y+3)2=4
所以选 C
【点睛】本题考查了根据圆心坐标和半径写出圆的方程,属于基础题.
8. 下列是全称命题且是真命题的是( )
A. ∀x∈R,x2>0 B. ∀x∈Q,x2∈Q
是
B
p 2 2 5+ = q 3 2>
p q q
p q p
p q p
p q p
p q p q p q
( ) ( )2 22 3 4x y+ + + = ( ) ( )2 22 3 9x y+ + − =
( ) ( )2 22 3 4x y− + + = ( ) ( )2 22 3 9x y− + + =
2r =
2r =
C. ∃x0∈Z,x >1 D. ∀x,y∈R,x2+y2>0
【答案】B
【解析】
主要考查全称量词和全称命题的概念.
解:A、B、D 中命题均为全称命题,但 A、D 中命题是假命题.故选 B.
9.某赛季,甲、乙两名篮球运动员都参加了 11 场比赛,他们每场得分的情况如图所示的茎叶
图表示,则甲、乙两名运动员得分的中位数分别为
A. 13、19
B. 19、13
C. 18、20
D. 20、18
【答案】B
【解析】
【分析】
由茎叶图分别得到甲、乙两运动员的得分,分别按照从小到大的顺序排列后可得所求的中位
数.
【详解】根据茎叶图中的数据,得甲运动员得分按从小到大的顺序排列为:6,8,9,15,
17,19,23,24,26,32,41,
所以甲运动员得分的中位数是 19;
乙运动员得分按从小到大的顺序排列为:5,7,8,11,11,13,20,22,30,31,40,
所以乙运动员得分的中位数是 13.
故选 B.
【点睛】本题考查茎叶图和样本数据的中位数的概念,解题的关键是从敬业图中的两运动员
的得分情况,然后再根据中位数的定义求解,属于基础题.
2
0
( )
10.记等差数列的前 项和为 ,若 ,则该数列的公差 ( )
A. 2 B. 3 C. 6 D. 7
【答案】B
【解析】
【详解】 ,
11. 从 1,2,3,4,5,6 这 6 个数字中,不放回地任取两数,两数都是偶数的概率是( )
A. B. C. D.
【答案】D
【解析】
从 1,2,3,4,5,6 这 6 个数中,不放回地任意取两个数,共有 C62=15 种结果,
其中满足条件两个数都是偶数的有(2,4),(2,6),(4,6)共 3 种情况.
不放回地任意取两个数,两个数都是奇数的概率 ,故选 D.
12. 一个游戏转盘上有四种颜色:红、黄、蓝、黑,并且它们所占面积的比为 6∶2∶1∶4,则指针
停在红色或蓝色的区域的概率为( )
A. B. C. D.
【答案】B
【解析】
试题分析:红色区域和蓝色区域的面积总和占面积的 ,故所求概率为 .
考点:几何概型.
二、填空题(本大题共 4 小题)
13.某商店统计了最近 个月某商品 进份 与售价 (单位:元)的对应数据如表:
假设得到的关于 和 之间的回归直线方程是 ,那么该直线必过的定点是________.
的
n nS 2 44, 20S S= = d =
( ) ( ) ( )4 2 2 3 4 1 2 4 12 3S S S a a a a d d− − = + − + = = ⇒ =
1
2
1
3
1
4
1
5
3 1
15 5p = =
6
13
7
13
4
13
10
13
7
13
7
13
6 x y
x 3 5 2 8 9 12
y 4 6 3 9 12 14
x y y bx a+=
【答案】
【解析】
【分析】
根据回归方程必过点( ),计算出 即可求得答案.
【详解】 , 8,
∵回归方程必过点( ),
∴该直线必过的定点是
故答案为
【点睛】本题考查了回归方程,线性回归方程必过样本中心点( ),属于基础题.
14.设变量 满足约束条件 ,则 的最大值是_________.
【答案】18
【解析】
【分析】
画出可行域,通过向上平移基准直线 到可行域边界的位置,由此求得目标函数的
最大值.
【详解】画出可行域如下图所示,由图可知,目标函数 在点 处取得最大
值,且最大值为 .
( )6.5, 8
x y, x y,
3 5 2 8 9 12 13 6.56 2x
+ + + + += = = 4 6 3 9 12 14
6y
+ + + + += =
x y,
( )6.5, 8
( )6.5, 8
x y,
x y、
2 2
1
1
x y
x y
x y
− ≤
− ≥ −
+ ≥
2 3z x y= +
2 3 0x y+ =
2 3z x y= + ( )3,4A
6 12 18z = + =
【点睛】本小题主要考查利用线性规划求线性目标函数的最大值.这种类型题目的主要思路是:
首先根据题目所给的约束条件,画图可行域;其次是求得线性目标函数的基准函数;接着画
出基准函数对应的基准直线;然后通过平移基准直线到可行域边界的位置;最后求出所求的
最值.属于基础题.
15.若“ , ”是真命题,则实数 m 的取值范围是______ .
【答案】
【解析】
【分析】
根据一元二次不等式在 上恒成立可知其 ,由此构造不等式求得结果.
【详解】由命题为真可知: ,解得: 的取值范围为:
故答案为:
【点睛】本题考查根据命题的真假性求解参数范围的问题,涉及到一元二次不等式在 上恒
成立问题的求解;关键是明确若一元二次不等式在 上恒成立,则需确定开口方向和判别式.
16. 下列四个命题:
①∀x∈R,x2+2x+3>0;
x R∀ ∈ 2 2 0x x m− − >
( ), 1−∞ −
R ∆ < 0
4 4 0m∆ = + < 1m < − m∴ ( ), 1−∞ −
( ), 1−∞ −
R
R
②若命题“p∧q”为真命题,则命题 p、q 都是真命题;
③若 p 是 q 的充分而不必要条件,则 p 是 q 的必要而不充分条件.
其中真命题的序号为________.(将符合条件的命题序号全填上)
【答案】①②③
【解析】
主要考查全称量词和全称命题的概念、存在量词和特称命题的概念以及两种命题的否定命题
的写法与判断,考查简单逻辑联结词.
解:因为 >0,∀x∈R 都成立,所以①是真命题;p,q 全真,p∧q 才会
真,所以②是真命题;由充要条件的定义知③也是真命题,故填①②③.
三、解答题(本大题共 6 小题)
17.设有两个命题.命题 p:不等式 的解集是 ;命题 q:函数
在定义域内是增函数.如果 为假命题, 为真命题,求 a 的取值范围.
【答案】
【解析】
分析】
根据一元二次不等式的解集、指数函数单调性可分别求得 为真命题时 的范围;由复合
命题真假性可知 一真一假,则分别讨论两种情况得到结果.
【详解】若命题 为真,则 ,解得:
若命题 为真,则 ,解得:
为假命题, 为真命题 一真一假
若 真 假,则 ;若 假 真,则
的取值范围为
【点睛】本题考查根据复合命题真假性求解参数范围的问题,涉及到根据一元二次不等式的
解集求解参数范围、根据指数函数单调性求解参数范围的问题;关键是能够根据复合命题的
真假性确定两个命题的真假性.
18.某校学生社团组织活动丰富,学生会为了解同学对社团活动的满意程度,随机选取了 100
位同学进行问卷调查,并将问卷中的这 100 人根据其满意度评分值(百分制)按照[40,50),
[50,60),[60,70),…,[90,100]分成 6 组,制成如图所示频率分布直方图.
【
¬ ¬
2 22 3 ( 1) 2x x x+ + = + +
( )2 1 1 0x a x− + + ≤ ∅
( ) ( 1)xf x a= + p q∧ p q∨
] [( )3,0 1,− ∪ +∞
,p q a
,p q
p ( )21 4 0a∆ = + − < 3 1a− < <
q 1 1a + > 0a >
p q∧ p q∨ ,p q∴
p q 3 0a− < ≤ p q 1a ≥
a∴ ( ] [ )3,0 1,− +∞
(1)求图中 x 的值;
(2)求这组数据的中位数;
(3)现从被调查的问卷满意度评分值在[60,80)的学生中按分层抽样的方法抽取 5 人进行座
谈了解,再从这 5 人中随机抽取 2 人作主题发言,求抽取的 2 人恰在同一组的概率.
【答案】(1)0.02;(2)75;(3)0.4
【解析】
【分析】
(1)由面积和为 1,可解得 x 的值;
(2)由中位数两侧的面积相等,可解得中位数;
(3)列出所有基本事件共 10 个,其中符合条件的共 4 个,从而可以解出所求概率.
【详解】解:(1)由(0.005+0.010+0.030+0.025+0.010+x)×10=1,解得 x=0.02.
(2)中位数设为 m,则 0.05+0.1+0.2+(m-70)×0.03=0.5,解得 m=75.
(3)可得满意度评分值在[60,70)内有 20 人,抽得样本为 2 人,记为 a1,a2
满意度评分值在[70,80)内有 30 人,抽得样本为 3 人,记为 b1,b2,b3,
记“5 人中随机抽取 2 人作主题发言,抽出的 2 人恰在同一组”为事件 A,
基本事件有(a1,a2),(a1,b1),(a1,b2),(a1,b3),(a2,b1),(a2,b2),
(a2,b3),(b1,b2),(b1,b3),(b2,b3)共 10 个,A 包含的基本事件个数为 4 个,
利用古典概型概率公式可知 P(A)=0.4.
【点睛】本题主要考查频率分布直方图,中位数和古典概型,属于基础题.
19.(1)经统计,在某储蓄所一个营业窗口排队等候的人数及相应概率如下:
排队人数 0 1 2 3 4 5 人及 5 人以上
概率
求至少 3 人排队等候的概率是多少?
(2)在区间 上随机取两个数 m,n,求关于 x 的一元二次方程 有实根的概
率.
【答案】(1) ;(2) .
【解析】
【分析】
(1)根据和事件概率公式可直接求得结果;
(2)在平面直角坐标系中,点 构成面积为 的正方形区域;根据一元二次方程有实根,
可确定 ,结合 ,可根据线性规划知识得到可行域,且其面积为 ;根据几
何概型概率公式求得结果.
【详解】(1)设至少 人排队等候的概率为 ,有 人排队等候的概率为 ,有 人排队
等候的概率为 ,有 人及 人以上排队等候的概率为
则
(2)在平面直角坐标系中,以 轴和 轴分别表示 值
在 内与图中正方形内的点一一对应,即正方形内的所有点构成全部试验结果的区
域,其面积为
设事件 为“关于 x 的一元二次方程 有实根”,则有
所对应的区域为图中的阴影部分
的
0.1 0.16 0.3 0.3 0.1 0.04
( )0,1 2 0x nx m− + =
0.44 1
8
( ),m n 1
0∆ ≥ ( ), 1,1m n∈ − 1
8
3 P 3 ( )3P 4
( )4P 5 5 ( )5P
( ) ( ) ( )3 4 5 0.3 0.1 0.04 0.44P P P P= + + = + + =
x y ,m n
,m n ( )0,1
1
A 2 0x nx m− + =
( )2
4
1 1
1 1
n m
n
m
− ≥− < <
− < <
阴影部分的面积为
故关于 的一元二次方程 有实根的概率为
【点睛】本题考查概率部分的和事件概率问题的求解、几何概型面积型的求解;本题中的几
何概型问题,关键是能够明确有两个变量时,采用面积的方式,结合线性规划的知识来进行
求解》
20.已知四面体 中 面 , , 垂足为 , , 为
中点, ,
(1)求证: 面 ;
(2)求点 到面 的距离.
【答案】(1)见解析;(2)
【解析】
【分析】
(1)证明线面平行,需先证明线线平行,可从三角形的中位线定理证明线线平行,从而再证线面
平行.
(2)求点到面的距离用等体积法,由 ,分别算出 、 ,建立体积等式
关系即可求 到面 的距离.
1 1 112 4 8
× × = ( )
1
18
1 8P A∴ = =
x 2 0x nx m− + = 1
8
ABCD AB ⊥ BCD BC DC⊥ BE AD⊥ E E F
,AD CD 2AB BD= = 1CD =
AC BEF
B ACD
2 21
7
A BCD B ACDV V− −= ∆BCDS ACDS∆
B ACD
【详解】、
(1)因为 , 所以 为 中点,又因为 是 中点,所以 ,
而 面 , 面 ,所以 面 .
(2)由已知得 , , ,
所以三角形 为直角三角形其面积 ,
三角形 的面积
设点 到面 的距离为 ,因为 ,
即
解得 ,
所以点 到面 的距离为 .
【点睛】(1)线面平行的判定定理是:若平面外的一条直线与平面内的一条直线平行,那么这
条直线与这个平面平行,即 .
(2)用等体积法求点到平面的距离主要是一个转换的思想,先用简单的方法求出四面体的体
积,然后计算出底面三角形的面积,再根据四面体体积公式 V=-Sh 求出点到平面的距离 .
21.已知圆 x2+y2=8 内有一点 P0(-1,2),AB 为过点 P0 且倾斜角为 α 的弦.
(1)当 α= 时,求 AB 的长;
(2)当弦 AB 被点 P0 平分时,写出直线 AB 的方程(用直线方程的一般式表示).
【答案】(1) ;(2)x-2y+5=0
【解析】
【分析】
BE AD⊥ AB BD= E AD F CD AC EF
AC ⊄ BEF EF ⊂ BEF AC BEF
3BC = 2 2AD = 7AC =
ACD 7
2ACDS∆ =
BCD 3
2BCDS∆ =
B ACD h A BCD B ACDV V− −=
1 123 3BCD ACDS S h∆ ∆× = ×
2 21
7h =
B ACD 2 21
7
a b
a a
b
α α
α
∉ ⇒
∈
h
3
4
π
30
(1)先求出直线 的方程,再利用垂径定理求解即可.
(2) 当弦 AB 被点 P0 平分时利用 得出 的斜率,再用点斜式求解化简成一般方程
即可.
【详解】(1)过点 O 做 OG⊥AB 于 G,连结 OA,当 α=135°时,直线 AB 的斜率为-1,
故直线 AB 的方程 x+y-1=0, ∴OG= ,
∵ , ∴
(2)当弦 AB 被点 P0 平分时,OP0⊥AB, 直线 OP0 的斜率为-2,所以直线 AB 的斜率为 .根
据直线的点斜式方程,直线 AB 的方程为 ,即 x-2y+5=0.
【点睛】本题主要考查了直线与圆的位置关系,常用垂径定理与斜率关系等,属于中等题型.
22.已知等差数列 的首项 ,公差 ,且第 2 项、第 5 项、第 14 项分别是一个等比
数列的第 2 项、第 3 项、第 4 项.
(1)求数列 的通项公式;
(2)设 , ,求 .
【答案】(1) ;(2)
【解析】
【分析】
(1)利用等差数列通项公式和等比中项的定义可构造关于 和 的方程,由 和
可求得 ,根据等差数列通项公式得到结果;
AB
0OP AB⊥ AB
| 0 0 1| 2
22
+ − =
2 2r = 1 15 308 2 2 2OA = − = = | | 2 30AB OA= =
1
2
12 ( 1)2y x− = +
{ }na 1 1a = 0d >
{ }na
( ) ( )*1 N3n
n
b nn a
= ∈+ 1 2n nS b b b= + +…+ nS
( )2 1na n n N ∗= − ∈ ( )2 1n
nS n
= +
1a d 1 1a = 0d >
d
(2)根据(1)的结果得到 ,采用裂项相消的方式求得结果.
【详解】(1)由题意得: ,整理得:
,
(2)由(1)知:
【点睛】本题考查等差数列通项公式的求解、裂项相消法求解数列的前 项和的问题,涉及到
等比中项的应用;求和的关键是能够对通项公式进行准确的裂项,进而前后相消求得结果,
属于常考题型.
nb
( )( ) ( )2
1 1 113 4a d a d a d+ + = + 2
12a d d=
0d > 1 1a = 2d∴ = ( ) ( )1 1 2 1na a n d n n N ∗∴ = + − = − ∈
( ) ( )
1 1 1 1 1
3 2 1 2 1n
n
b n a n n n n
= = = − + + +
1 2n nS b b b∴ = + +⋅⋅⋅+ 1 1 1 1 1 112 2 2 3 1n n
= − + − +⋅⋅⋅+ − +
1 112 1n
= − +
( )2 1
n
n
= +
( )2 1n
nS n
∴ = +
n