- 1.56 MB
- 2021-04-14 发布
www.ks5u.com
嘉善高级中学高一数学月考检测试卷
一、选择题 (每题4分,共40分)
1.已知全集U={1,2,3,4,5,6,7},A={3,4,5},B={1,3,6},则A∩(CUB)等于( )
A. {4,5} B. {2,4,5,7} C. {1,6} D. {3}
【答案】A
【解析】
试题分析:根据题意,由于全集U={1,2,3,4,5,6,7},A={3,4,5},B={1,3,6}那么可知,CUB={2,4,5,7},则A∩(CUB)= {4,5},故选A.
考点:交、并、补的定义
点评:本题考查利用交、并、补的定义进行集合间的混合运算,属于基础题
2.函数的定义域为( )
A. B. C. D.
【答案】C
【解析】
【分析】
根据对数的定义和对数的真数为正数,可得不等式组,解这个不等式即可求出函数的定义域.
【详解】由题意可知:.
故选:C
【点睛】本题考查了对数型函数的定义域,忽略对数型函数底数的要求是易犯的错误,考查了数学运算能力.
3.的次方根是( )
A. B. C. D.
【答案】C
【解析】
【分析】
根据偶次方根的定义可以直接求解.
【详解】的次方根是.
故选:C
【点睛】考查了偶次方根的定义,属于基础题.
4.若函数为定义在R上的奇函数,且在内是增函数,又,则不等式的解集为( )
A. B. C. D.
【答案】D
【解析】
【分析】
利用奇函数的单调性的性质,可以知道函数在上的单调性,结合的值可以知道的值,分类讨论求出的解集.
【详解】奇函数在内是增函数,所以函数在内是增函数,
.
当时,则有,
当时, 则有,所以的解集为
.
故选:D
【点睛】本题考查了利用函数奇偶性和单调性求解不等式解集问题.
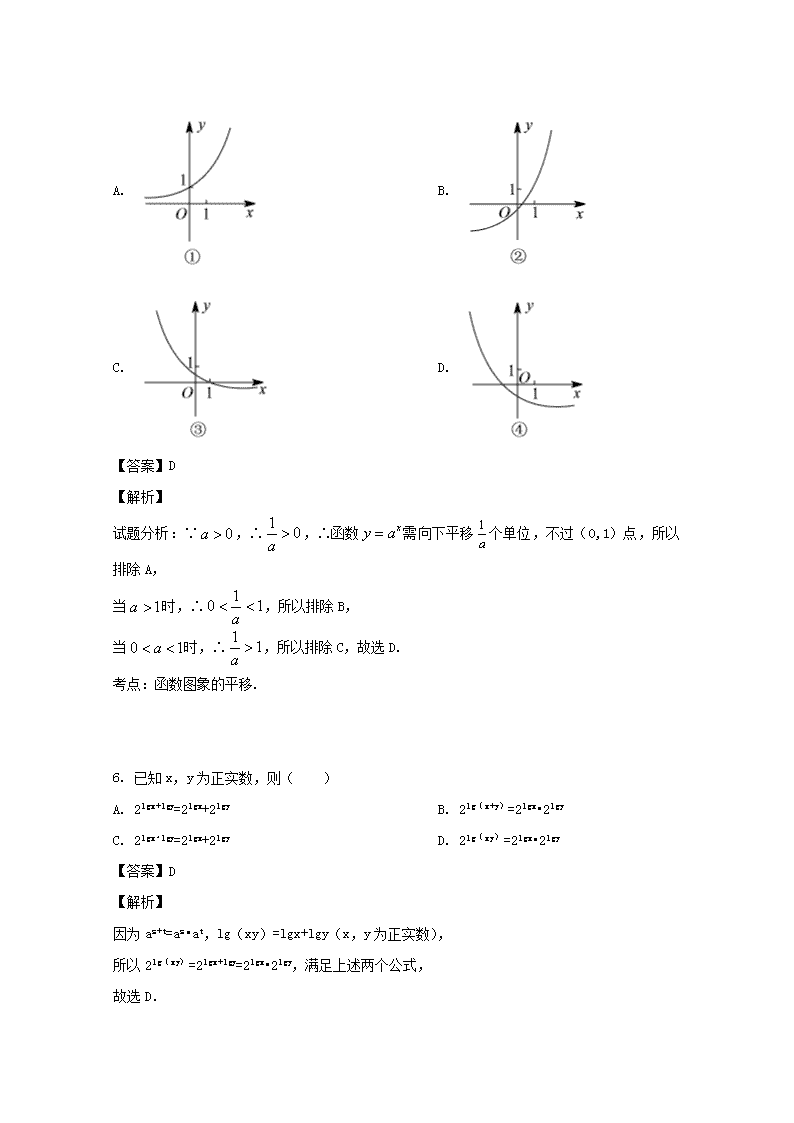
5.函数的图像可能是( ).
A. B.
C. D.
【答案】D
【解析】
试题分析:∵,∴,∴函数需向下平移个单位,不过(0,1)点,所以排除A,
当时,∴,所以排除B,
当时,∴,所以排除C,故选D.
考点:函数图象的平移.
6. 已知x,y为正实数,则( )
A. 2lgx+lgy=2lgx+2lgy B. 2lg(x+y)=2lgx•2lgy
C. 2lgx•lgy=2lgx+2lgy D. 2lg(xy)=2lgx•2lgy
【答案】D
【解析】
因为as+t=as•at,lg(xy)=lgx+lgy(x,y为正实数),
所以2lg(xy)=2lgx+lgy=2lgx•2lgy,满足上述两个公式,
故选D.
7.若,则下列不可能成立的是( )
A. B. C. D.
【答案】D
【解析】
【分析】
设,化为对数式,根据的不同取值进行判断,选出正确答案.
【详解】设,则有,
当时,有;
当时,有;
当时,有.
故选:D
【点睛】本题考查了两个指数式相等判断指数大小的问题,考查了指数式和对数式的互化,考查了数学运算能力.
8.已知,则满足下列关系式( )
A. B. C. D.
【答案】B
【解析】
【分析】
把指数式化成对数式,利用对数的运算性质可以求出满足的关系式.
【详解】,
所以有.
故选:B
【点睛】本题考查了对数式与指数式的互化,考查了对数运算的性质,
考查了数学运算能力和数感能力.
9.若函数 在上单调递减,则实数的取值范围为( )
A. B. C. D.
【答案】A
【解析】
【分析】
根据分段函数的单调性的性质可以得到不等式组,解这个不等式组即可.
【详解】因为是上单调递减函数,
所以有:.
故选:A
【点睛】本题考查了已知分段函数的单调性求参数取值范围问题,考查了数学运算能力.
10.设最小值为,的最大值为.若函数,,则( )
A. B. C. D.
【答案】B
【解析】
【分析】
通过比较函数和函数的大小,化简函数的解析式,然后分别求出函数的最小值和最大值,最后计算得出的值.
【详解】,
当时, ,此时函数的最小值为-4,
当时, ,此时,综上:;
,
当时, ,此时函数的最大值为12,
当时, ,此时
,
综上:,
.
故选:B
【点睛】本题考查了分段函数的最值问题,考查了分类讨论思想,考查了数学运算能力.
二、填空题(双空每题3分,单空每空4分,共36分)
11.化简:_________,__________.
【答案】 (1). 6 (2). 10
【解析】
【分析】
运用根式与指数互化公式和指数的运算公式求解即可.
【详解】;
.
故答案为:6;
【点睛】本题考查了根式与指数式的互化,考查了指数的运算法则,考查了数学运算能力.
12.若函数定义域为,则函数定义域为_________,函数定义域为_____________.
【答案】 (1). (2).
【解析】
【分析】
由函数定义域为,可以求出的取值范围,也就求出函数定义域,这样也能求出定义域.
【详解】因为函数定义域为,所以有,所以函数定义域为
;
,即函数定义域为:.
故答案为:;
【点睛】本题考查了求函数的定义域,考查了数学运算能力.
13.若函数f(x)=(2a-1)x-3-2,则y=f(x)的图象恒过定点______,又f(x)在R上是减函数,则实数a的取值范围是______.
【答案】 (1). (3,-1) (2). (,1)
【解析】
【分析】
令,求得,进而求得的值,即可得函数图象经过定点的坐标,再根据在上是减函数,故有,由此求得实数的取值范围
【详解】解:对于函数,
令,得,则,可得的图象恒过定点,
又∵函数在上减函数,故有,求得,
故答案为;
【点睛】本题考查指数函数恒过定点问题,考查指数函数的单调性,属于基础题
14.在如图所示的韦恩图中,是非空集合,定义表示阴影部分集合,若集合,,则=____________;
=____________;
【答案】 (1). (2).
【解析】
【分析】
求出函数的定义域化简集合的表示,求出函数的值域化简集合的表示,根据定义结合数轴求出及.
【详解】由,所以,
当时, ,所以.
所以,.
故答案为:;
【点睛】本题考查了集合新定义题,考查了集合的交集、补集的运算,考查了求函数的定义域和值域.
15.已知是奇函数,当时,,则当时,_______;
【答案】
【解析】
【分析】
根据奇函数的定义可以直接求出当时的表达式
【详解】当时, ,所以有.
故答案为:
【点睛】本题考查了利用奇函数的性质求解函数解析式,考查了数学运算能力.
16.若关于的方程有实数解,则实数的取值范围是________
【答案】
【解析】
【分析】
令,求出的取值范围,对等式进行换元,常变量分离,利用二次函数的单调性可以求出实数的取值范围.
【详解】令, 因为,所以.因此有:,方程可以化为:
.
故答案为:
【点睛】本题考查了方程有实数解求参数取值范围问题,考查了换元法、二次函数、指数函数的值域问题,考查了数学运算能力.
17.设,若恰有3个不同的实根,且其中三个根,则的取值范围是________.
【答案】
【解析】
【分析】
在直角坐标系内,画出函数的图象,结合已知利用图象求出三个根的分布情况、对称情况,最后求出取值范围.
【详解】在直角坐标坐标系内画出函数的图象, 如下图所示:
恰有3个不同的实根,于是有,设三个根据从左到右分别为,当
时,且,有,当时,且,有,
所以有,显然有 关于直线,则有
, 因此有的对值范围为:
.
故答案为:
【点睛】本题考查了求方程实根和问题,画出图象利用数形结合思想是解题的关键.
三:解答题.
18.设函数的定义域为集合,函数的值域为集合.
(1)求集合,;
(2)若全集,集合,满足,求实数的取值范围.
【答案】(1) ,;(2) .
【解析】
【分析】
(1)根据被开方数为非负数,解不等式可求出集合,利用指数函数的单调性可以求出集合;
(2)根据集合交集运算的性质可得之间的关系,利用数轴求出实数的取值范围.
【详解】(1)由,所以.
当,所以;
(2)因为,所以,又因为,
所以,因此有:.
【点睛】本题考查了函数的定义域和值域,考查了集合的补集运算,考查了根据集合的运算结果求参数取值范围.
19.已知函数为奇函数.
(1)求的值;
(2)当时,求的解集.
【答案】(1) ;(2) .
【解析】
【分析】
(1)根据奇函数的定义,可以求出的值;
(2)判断函数的单调性,利用单调性的奇偶性求出解集.
【详解】(1) 因为函数为奇函数,所以,即
;
(2)因为,所以,因此.
设是任意两个实数且.
,
因为,所以,,因此,所以函数
是单调递增函数.
【点睛】本题考查了已知函数的奇偶性求参数问题,考查了函数单调性的判断,考查了数学运算能力.
20.已知,定义函数:.
(1)画出函数的图象并写出其单调区间;
(2)若,且对恒成立,求的取值范围.
【答案】(1) 函数在上单调递减, 在上单调递增;
(2) .
【解析】
【分析】
(1)在直角坐标系内画出图象即可,通过图象可以写出单调区间;
(2)利用函数的单调性化简不等式,最后利用绝对值不等式的解集公式进行求解即可.
【详解】(1)图象如下图所示:通过图象可知:函数在上单调递减, 在上单调递增;
(2) 在恒成立,
于是有:且在恒成立,
因为,所以,于是有:.
【点睛】本题考查了画函数图象,考查了不等式恒成立问题,考查了数学运算能力.
21.已知是定义在上的单调函数,且满足,且.
(1)求的值并判断的单调性和奇偶性;
(2)若恒成立,求的取值范围.
【答案】(1) 函数是奇函数,是单调递增函数;(2) .
【解析】
【分析】
(1)令可以求出的值,令可以判断出奇偶性,根据和的值结合已知可以判断出函数的单调性;
(2)利用函数的单调性可以得到不等式,常变量分离,利用基本不等式,可以求出的取值范围.
【详解】(1) 令,可得令,所以有
,因此函数奇函数.
由已知可知:是定义在上的单调函数,且,因此函数是上的单调递增函数;
(2)因为函数是奇函数,所以由可得
,可得:,
因为(当且仅当取等号),所以要想
恒成立,只需.
【点睛】本题考查了抽象函数的单调性和奇偶性的判断,考查了用基本不等式判断不等式恒成立问题.
22.已知函数 (实常数).
(1)设在区间的最小值为,求的表达式;
(2)若在区间上单调递增,求的取值范围.
【答案】(1) ;(2) .
【解析】
【分析】
(1)根据正负性,结合具体类型的函数的单调性,进行分类讨论可以求出的表达式;
(2)利用函数单调性定义,转化为不等式恒成立问题,利用分类讨论思想可以求出的取值范围.
【详解】(1)当时, ,函数在区间的最小值为;
当时,函数的对称轴为:.
若,在区间的最小值为;
若,在区间的最小值为
;
若,在区间的最小值为;
当时, ,在区间的最小值为.
综上所述:;
(2) .设是上任意两个实数,且.
,要想函数
在区间上单调递增只需.
由.
当,不等式显然成立;
当时, ,要想恒成立,只需;
当时, ,要想恒成立,只需,
综上所述:的取值范围:.
【点睛】本题考查了求函数在区间上的最小值问题,考查了已知函数在区间上的单调性求参数取值范围问题,考查了分类讨论思想.