- 248.00 KB
- 2021-04-14 发布
第九章小结与思考(1)
【学习目标】1.掌握有关单项式乘单项式、单项式乘多项式、多项式乘多项式的计算法则,并会应用法则进行运算;2.进一步感受从图形面积计算得出整式乘法法则、公式的过程,并能理解算理,学会有条理的思考和表达。
【预习研问】
A 1.单项式乘单项式的法则是把 之积作为积的系数,相同字母的 作为积里这个字母的指数,只在一个单项式中含有的字母,则连同其指数作为积的一个 。
A 2.单项式与多项式相乘,就是根据乘法 律,用单项式乘多项式的 ,再把所得的 。
A 3.多项式与多项式相乘,先用一个多项式的 乘另一个多项式的 再把所得的 。
A 4. 写出完全平方公式 ;
写出平方差公式 。
A 5.填空
(1)_______; (2)_______;
(3) ; (4) ;
(5) ; (6)
B 6.计算
(1) (2)
个人或小组的预习未解决问题:
【课内解问】
A 1.下列关于单项式与多项式相乘的说法中不正确的是 ( )
A.单项式之积不可能是多项式 B.单项式必须是同类项才能相乘
C.几个单项式相乘有一个式子为零,积一定为零 D.几个单项式之积仍是单项式
A 2.在下列多项式乘法中,能用平方差公式计算的是 ( )
A.(1+x)(x+1) B.( C.(-a+b)(a-b) D.(
B 3.若,则之值为何( )
A.18 B.24 C.39 D. 45
B 4.填空 (1)(x-4y)2+ =(x+4y)2 ;(2)(m+n)2- =(m-n)2 ;
(3)a2+b2+ =(a-b)2 ; (4)x2-x+( )=( )2 。
B 5.若a+,则= ;若 求 = 。
B 6.根据乘法公式计算:102×98=( )( )=( )2-( )2= 。
A 7.计算:
(1); (2); (3)
B 8.化简后求值:,其中,。
A9.分别计算图中阴影部分的面积:
B 10.说理:试说明不论x,y取什么有理数,多项式的值总是正数.
【课后答问】
A 1.计算: = ;(2x+5)(x-5) = .
A 2.计算:(3x-2)2= ;(—a+2b)(a+2b)= .
A 3.计算: ;(用科学记数法表示).
A 4.⑴ ·; ⑵
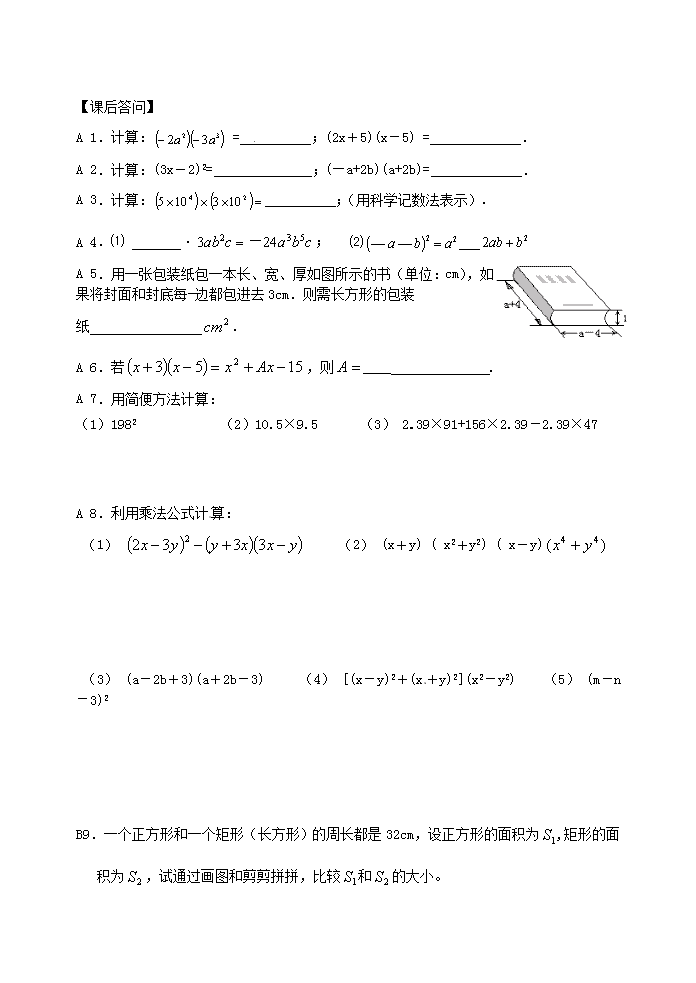
A 5.用一张包装纸包一本长、宽、厚如图所示的书(单位:cm),如果将封面和封底每一边都包进去3cm.则需长方形的包装
纸 .
A 6.若,则____ .
A 7.用简便方法计算:
(1)1982 (2)10.5×9.5 (3) 2.39×91+156×2.39-2.39×47
A 8.利用乘法公式计算:
(1) (2) (x+y) ( x2+y2) ( x-y)
(3) (a-2b+3)(a+2b-3) (4) [(x-y)2+(x+y)2](x2-y2) (5) (m-n-3)2
B 9.一个正方形和一个矩形(长方形)的周长都是32cm,设正方形的面积为,矩形的面积为,试通过画图和剪剪拼拼,比较和的大小。