2020届高三数学上学期期末考试质量检测试题 理（含解析） 13页

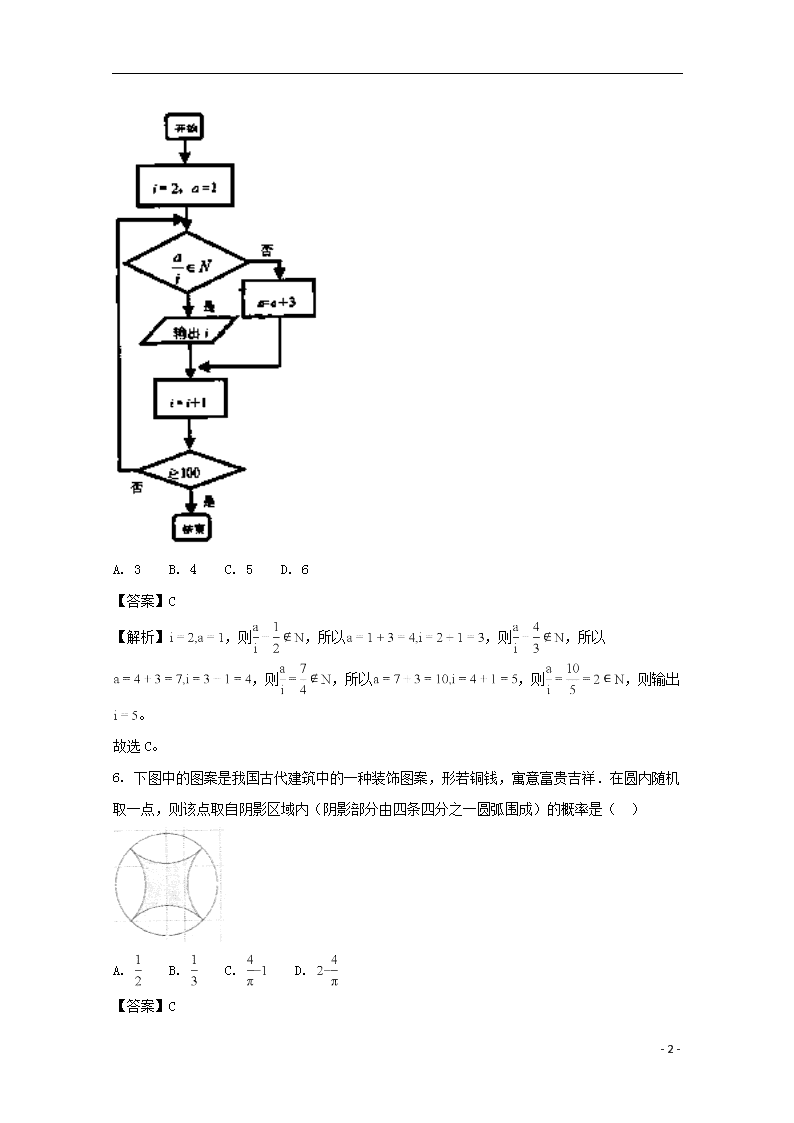
亳州市2017-2019学年度第一学期期末高三质量检测 数学试卷（理）‎ 第Ⅰ卷 一、选择题：本大题共12小题,每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1. 已知集合，集合，则（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】，故选B。‎ ‎2. 已知复数（为虚数单位），则（ ）‎ A. B. C. 2 D. ‎ ‎【答案】A ‎【解析】，所以，故选A。‎ ‎3. 已知是第二象限角，，则（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎.....................‎ 则，故选D。‎ ‎4. 已知是定义在上的奇函数，是定义在上的偶函数，若，则（ ）‎ A. 0 B. 2 C. -2 D. 4‎ ‎【答案】A ‎【解析】，所以是奇函数，‎ 所以，故选A。‎ ‎5. 执行下面的程序框图，则输出的第1个数是（ ）‎ - 13 -‎ A. 3 B. 4 C. 5 D. 6‎ ‎【答案】C ‎【解析】，则，所以，则，所以，则，所以，则，则输出。‎ 故选C。‎ ‎6. 下图中的图案是我国古代建筑中的一种装饰图案，形若铜钱，寓意富贵吉祥．在圆内随机取一点，则该点取自阴影区域内（阴影部分由四条四分之一圆弧围成）的概率是（ ）‎ A. B. C. D. ‎ ‎【答案】C - 13 -‎ ‎【解析】令圆的半径为1，则，故选C。‎ ‎7. 由函数的图像变换得到函数的图像，则下列变换过程正确的是（ ）‎ A. 把上各点的横坐标缩短到原来的倍，纵坐标不变，再把得到的曲线向右平移个单位长度，得到曲线 B. 把上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移个单位长度，得到曲线 C. 把向右平移个单位长度，再把得到的曲线上各点的横坐标缩短到原来的倍，纵坐标不变，得到曲线 D. 把向右平移个单位长度，再把得到的曲线上各点的横坐标伸长到原来的2倍，纵坐标不变，得到曲线 ‎【答案】D ‎【解析】，‎ 所以变换过程是：先向右平移个单位长度，在将各点的横坐标伸长到原来的2倍，纵坐标不变，得到。‎ 故选D。‎ ‎8. 经过双曲线的左焦点作倾斜角为的直线，若交双曲线的左支于，则双曲线离心率的取值范围是（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】由题意，，得，所以，即离心率的范围是，故选B。‎ ‎9. 如下图，网格纸上小正方形的边长为1，粗实线画出的是某组合体的三视图，则该组合体的体积为（ ）‎ - 13 -‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】，故选A。‎ ‎10. 的展开式中常数项是（ ）‎ A. -15 B. 5 C. 10 D. 15‎ ‎【答案】B ‎【解析】二项式的展开通项为，‎ 当时，有；当时，有；当时，有，‎ 所以，常数项为，故选B。‎ 点睛：本题考查二项式定理的应用。本题中的二项式形式较为复杂，为两式相乘的形式，一般的，将简单的一项直接展开，得，之后只需分别求解对应项的系数即可。‎ ‎11. 椭圆的两个焦点为，椭圆上两动点总使为平行四边形，若平行四边形的周长和最大面积分别为8和，则椭圆的标准方程可能为（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】C ‎【解析】由周长为8，可知，‎ 由最大面积为，可知，‎ - 13 -‎ 所以椭圆方程可以是，故选C。‎ 点睛：本题考查椭圆的性质应用。本题中的平行四边形的基本型是焦点三角形，考查焦点三角形相关特征的应用，得，，利用即可解得标准方程。‎ ‎12. 已知函数，若存在四个互不相等的实数根，则实数的取值范围为（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】D ‎【解析】令，则，由题意，有两个不同的解，有两个不相等的实根，‎ 由图可知，得或，所以和各有两个解。‎ 当有两个解时，则，‎ 当有两个解时，则或，‎ 综上，的取值范围是，故选D。‎ 第Ⅱ卷 二、填空题：本大题共4小题，每小题5分，把答案填在答题卡的相应位置．‎ ‎13. 已知实数满足，则的最小值为__________．‎ - 13 -‎ ‎【答案】-2‎ ‎【解析】‎ 由图，可知过点时，由最小值。‎ ‎14. 已知平面向量满足，，若的夹角为，则__________．‎ ‎【答案】3‎ ‎【解析】，得，所以。‎ ‎15. 的内角所对的边分别为，若，则角__________．‎ ‎【答案】‎ ‎【解析】，得，‎ 所以，所以。‎ ‎16. 某产品包装公司要生产一种容积为的圆柱形饮料罐（上下都有底），一个单位面积的罐底造价是一个单位面积罐身造价的3倍，若不考虑饮料罐的厚度，欲使这种饮料罐的造价最低，则这种饮料罐的底面半径是__________．‎ ‎【答案】‎ ‎【解析】，则，，‎ 所以，‎ 所以在单调递减，单调递增，‎ 所以当时，造价最低。‎ 点睛：本题考查导数的实际应用。本题中首先根据题目，得到造价的函数方程，则通过求导来判断造价的最小值，通过求导分析，得到 - 13 -‎ 的单调性情况，解得答案。‎ 三、解答题：解答应写出文字说明、证明过程或演算步骤. ‎ ‎17. 已知数列的前项和满足，其中是不为零的常数，．‎ ‎（Ⅰ）求的通项公式；‎ ‎（Ⅱ）若，记，求数列的前项和．‎ ‎【答案】（Ⅰ）（Ⅱ） ‎ ‎【解析】试题分析：（1）由已知可得：，两式相减化简得；（2），所以，得。‎ 试题解析：‎ ‎（Ⅰ）由已知可得：‎ 两式相减得：，即 ‎∵∴∴∴‎ ‎∴是首项为，公比为3的等比数列，从而 ‎（Ⅱ）因为，所以，从而 ‎∴‎ ‎∴‎ 点睛：本题考查数列基本型的综合应用。首先考查型求通项的公式应用，求解通项；然后考察裂项相消求和，需要对裂项基本型要熟悉：，解得答案。‎ ‎18. 某超市在元旦期间开展优惠酬宾活动，凡购物满100元可抽奖一次，满200元可抽奖两次…依此类推．抽奖箱中有7个白球和3个红球，其中3个红球上分别标有10元，10元，20元字样．每次抽奖要从抽奖箱中有放回地任摸一个球，若摸到红球，根据球上标注金额奖励现金；若摸到白球，没有任何奖励．‎ ‎（Ⅰ）一次抽奖中，已知摸中了红球，求获得20元奖励的概率；‎ - 13 -‎ ‎（Ⅱ）小明有两次抽奖机会，用表示他两次抽奖获得的现金总额，写出的分布列与数学期望．‎ ‎【答案】（Ⅰ）（Ⅱ）‎ ‎【解析】试题分析：（1）；（2）的可能取值为0,10,20,30,40，写出分布列，求出期望。‎ 试题解析：‎ ‎（Ⅰ）设事件，事件 则所求概率为 ‎（Ⅱ）的可能取值为0,10,20,30,40‎ ‎∴的分布列为 所以，．‎ ‎19. 如图，多面体中，是正方形，是梯形，，，平面且，分别为棱的中点．‎ - 13 -‎ ‎（Ⅰ）求证：平面平面；‎ ‎（Ⅱ）求平面和平面所成锐二面角的余弦值．‎ ‎【答案】（Ⅰ）见解析（Ⅱ）‎ ‎【解析】试题分析：（1）通过证明平面，所以平面平面．（2）建立空间直角坐标系，求出平面和平面的法向量，求二面角的余弦值。‎ 试题解析：‎ ‎（Ⅰ）∵，是正方形 ‎∴∵分别为棱的中点∴‎ ‎∵平面∴∵，‎ ‎∴平面∴从而 ‎∵，是中点∴‎ ‎∵∴平面 又平面 所以，平面平面．‎ ‎（Ⅱ）由已知，两两垂直，如图，建立空间直角坐标系，设，‎ 则，，，，‎ ‎∴，‎ 平面的一个法向量为，‎ 由得令，则 由（Ⅰ）可知平面 ‎∴平面的一个法向量为 设平面和平面所成锐二面角为，‎ 则 所以，平面和平面所成锐二面角的余弦值为．‎ - 13 -‎ ‎20. 已知抛物线与过点 的直线交于两点，且总有．‎ ‎（Ⅰ）确定与的数量关系；‎ ‎（Ⅱ）若，求的取值范围．‎ ‎【答案】（Ⅰ）（Ⅱ）‎ ‎【解析】试题分析：（1）设，由，，由得：，解得．（2）由题意，，，所以。‎ 试题解析：‎ ‎（Ⅰ）设，，‎ 由消去得：‎ ‎∴，‎ 由得：即 ‎∴∵∴．‎ ‎（Ⅱ）由（Ⅰ）可计算：‎ ‎ ‎ ‎∵‎ - 13 -‎ ‎∴‎ ‎∴‎ ‎∵∴‎ 点睛：本题考查直线和抛物线的位置关系。解析几何题型涉及到线段长，一般直接应用弦长公式，本题中首先设定目标直线，联立方程组，求得得到，利用函数求值域，由，解得。‎ ‎21. 已知．‎ ‎（Ⅰ）讨论的单调性；‎ ‎（Ⅱ）若在定义域内总存在使成立，求的最小值．‎ ‎【答案】（Ⅰ）见解析（Ⅱ）的最小值是．‎ ‎【解析】试题分析：（1）定义域为，，分类讨论得到单调性情况；（2）分参得到恒成立，令，求导得到在上单调减，在上单调增，所以，得。‎ 试题解析：‎ ‎（Ⅰ）定义域为，‎ ‎①当时，由解得：，由解得：‎ ‎∴在上单调递减，在上单调递增；‎ ‎②当时，由解得：或，由解得：‎ ‎∴在上单调递减，在和上单调递增；‎ ‎③当时，（仅在时等号成立）‎ ‎∴在上单调递增；‎ ‎④当时，由解得：或，由解得：‎ ‎∴在上单调递减，在和上单调递增．‎ ‎（Ⅱ）由已知，在定义域内总存在使成立，‎ 即，使成立 - 13 -‎ 令，则 ‎∴在上单调递增，在上单调递减 ‎∴‎ 所以，式转化为 使成立 即，‎ 令，则 ‎∴在上单调减，在上单调增 ‎∴‎ 所以， 即的最小值是．‎ 请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.‎ ‎22. 选修4-4：坐标系与参数方程 在直角坐标系中，曲线（为参数），在以为极点，轴的非负半轴为极轴的极坐标系中，曲线．‎ ‎（Ⅰ）写出曲线和的普通方程；‎ ‎（Ⅱ）若曲线上有一动点，曲线上有一动点，求使最小时点的坐标．‎ ‎【答案】（Ⅰ），（Ⅱ）‎ ‎【解析】试题分析：（1），；（2）设，结合图形可知：最小值即为点到直线的距离的最小值．到直线的距离，所以的坐标为。‎ 试题解析：‎ ‎（Ⅰ），‎ ‎（Ⅱ）设，结合图形可知：最小值即为点到直线的距离的最小值．‎ ‎∵到直线的距离 ‎∴当时，最小，即最小．‎ - 13 -‎ 此时，，结合可解得：，‎ 即所求的坐标为 ‎23. 选修4-5：不等式选讲 已知函数．‎ ‎（Ⅰ）解关于的不等式；‎ ‎（Ⅱ）对于，都有成立，求实数的取值范围．‎ ‎【答案】（Ⅰ）（Ⅱ）‎ ‎【解析】试题分析：（1）或，得不等式解集为；（2）时，恒成立，在和上单调递增，得，所以。‎ 试题解析：‎ ‎（Ⅰ）由得：‎ ‎∴即或 解得：或 所以，不等式解集为 ‎（Ⅱ）由，都有成立可得：‎ 时，恒成立 ‎∵在和上单调递增 ‎∴‎ ‎∴时，‎ ‎∴‎ ‎ ‎ - 13 -‎