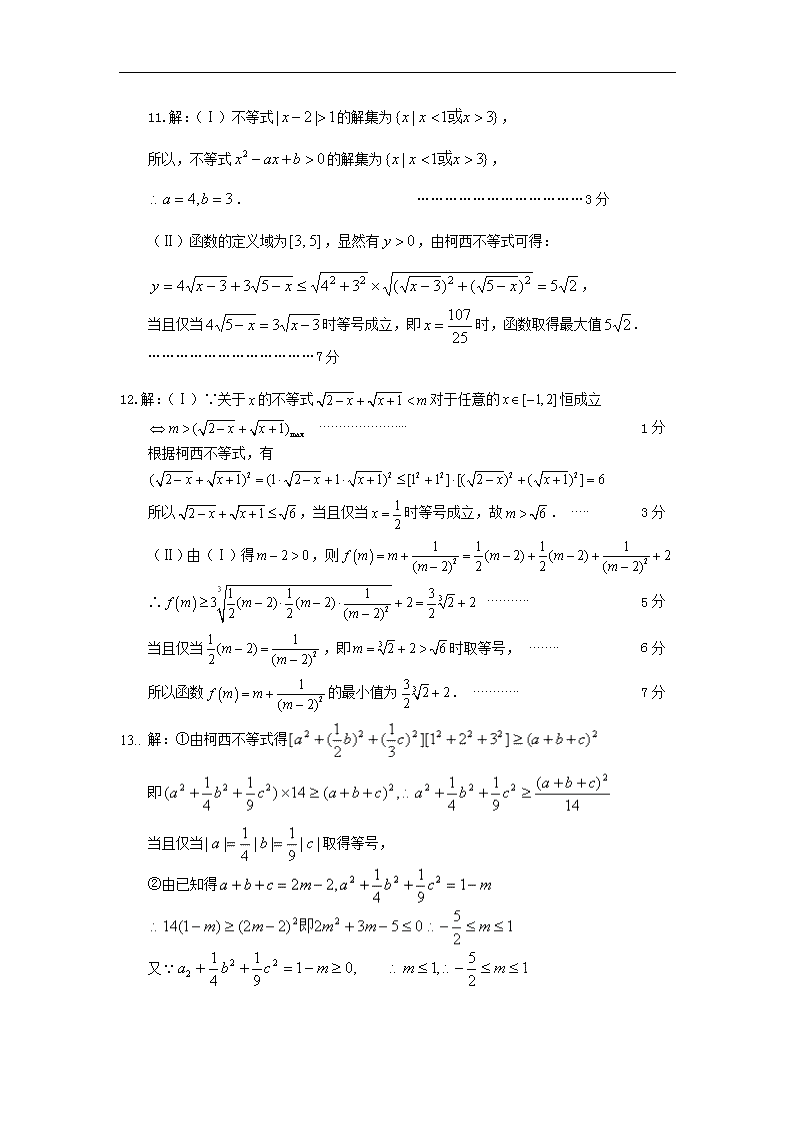高考数学专题复习：不等式精选精练答案 4页

‎2. 解：(I)所以的最小值为3．……………4分 ‎(II) 由(I)可知，当时，，即，此时；‎ 当时，，即，此时．‎ 因此不等式的解集为为或． …………………7分 ‎3. 解：由柯西不等式得 ‎ ‎ ‎（当且仅当即等号成立）‎ ‎4. ‎ ‎5. （I），得 ‎ 不等式的整数解为2， ‎ ‎ ‎ 又不等式仅有一个整数解2，整数 …………4分 ‎（II）即解不等式，．‎ 当时，不等式，不等式解集为 ‎ 当时，不等式为，不等式解为 ‎ 当时， ，不等式解集为 ‎ 综上，不等式解为 …………7分 ‎6.（1）由题设知：，‎ 如图，在同一坐标系中作出函数和的 图象（如图所示）,知定义域为.………4分 ‎（2）由题设知，当时，恒有，‎ 即， 又由（1），∴ ……7分 ‎7. （Ⅰ）‎ 当时，；‎ 当时，，‎ 所以，即当时，. 4分 ‎（Ⅱ）由且是正实数，根据柯西不等式，得 ‎，‎ 即. 7分 ‎8 略 ‎9略 ‎ ‎10. 本题主要考查绝对值的含义、柯西不等式等基础知识，考查运算求解能力以及推理论证能力，考查函数与方程思想以及分类与整合思想.满分7分.‎ 解析：（Ⅰ）当时，由得，所以； ‎ 当时，由得，所以； ‎ 当时，由得，所以. ……2分 综上得：不等式的解集. ……3分 ‎（Ⅱ）， ……4分 由柯西不等式得， m][来源:学|科|网Z|X|X|K]‎ ‎， ……5分 当且仅当时取“=”， ‎ ‎ 的取值范围是. ……7分 ‎11.解：（Ⅰ）不等式的解集为，‎ 所以，不等式的解集为，‎ ‎．　　　　　　　　　　　　………………………………3分 ‎（Ⅱ）函数的定义域为，显然有，由柯西不等式可得：‎ ‎，‎ 当且仅当时等号成立，即时，函数取得最大值.‎ ‎………………………………7分 ‎12.解：（Ⅰ）∵关于的不等式对于任意的恒成立 ‎ 1分 根据柯西不等式，有 所以，当且仅当时等号成立，故． 3分 ‎（Ⅱ）由（Ⅰ）得，则 ‎∴ 5分 当且仅当，即时取等号， 6分 所以函数的最小值为． 7分 ‎13.. 解：①由柯西不等式得 即 当且仅当取得等号， ‎ ‎②由已知得 又 ‎ ‎14. 解: （Ⅰ）,‎ ‎.…………………………3分 ‎,‎ 即 ‎.……………………7分