- 671.50 KB
- 2021-04-14 发布
云南省昆明市官渡区第一中学2018-2019学年高二下学期期中考试
文科数学试题
试卷满分:150分 考试时间:120分钟
第I卷
一、选择题(本大题共12小题.每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在答题卡上)
1、已知集合A=﹛-2,0,2﹜,B=﹛|--﹜,则AB=
(A) (B) (C) (D)
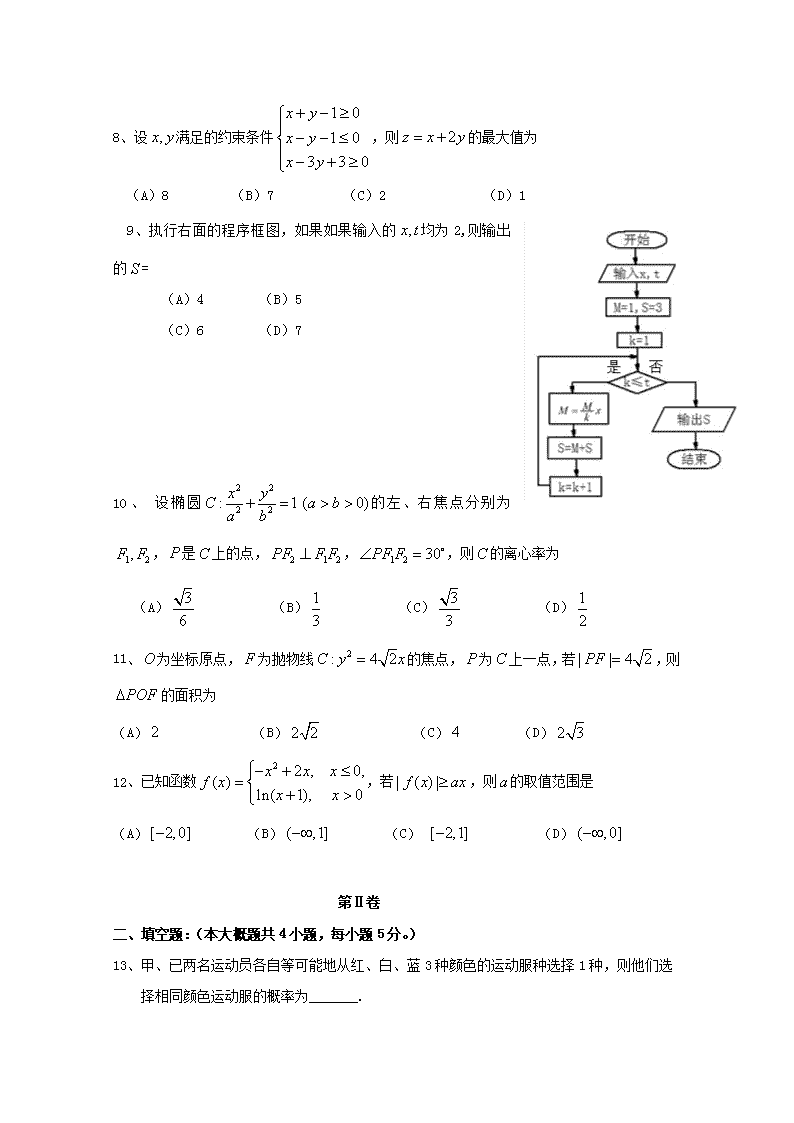
2、
(A) (B) (C) (D)
3、已知命题,;命题,,则下列命题中为真命题的是:
(A) (B) (C) (D)
4、设向量,满足,,则a·b=
(A)1 (B) 2 (C)3 (D) 5
5、等差数列的公差为2,若,,成等比数列,则的前n项和=
(A) (B) (C) (D)
6、如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm,高为6c m的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为
(A) (B) (C) (D)
7、正三棱柱的底面边长为2,侧棱长为,D为BC中点,则三棱锥的体积为
(A)3 (B) (C)1 (D)
8、设满足的约束条件,则的最大值为
(A)8 (B)7 (C)2 (D)1
9、执行右面的程序框图,如果如果输入的均为2,则输出的=
(A)4 (B)5
(C)6 (D)7
10、 设椭圆的左、右焦点分别为,是上的点,,,则的离心率为
(A) (B) (C) (D)
11、为坐标原点,为抛物线的焦点,为上一点,若,则的面积为
(A) (B) (C) (D)
12、已知函数,若,则的取值范围是
(A) (B) (C) (D)
第Ⅱ卷
二、 填空题:(本大概题共4小题,每小题5分。)
13、甲、已两名运动员各自等可能地从红、白、蓝3种颜色的运动服种选择1种,则他们选择相同颜色运动服的概率为_______.
14、函数的最大值为_________.
15、过双曲线左焦点的直线交双曲线的左支于两点, 为其右焦点,则的值为 .
16、已知为偶函数,当 时,,则曲线在点处的切线方程______________________.
三、解答题:(解答应写出文字说明过程或演算步骤。)
17、(本小题满分10分)
已知分别为内角的对边,
(Ⅰ)若,求;
(Ⅱ)设,且,求的面积
18、(本小题满分12分)
如图,四棱锥中,底面为矩形,垂直于面,为的中点。
(I)证明:;
(II)设,三棱锥的体积,求到平面的距离.
19、(本小题满分12分)
已知是等差数列,满足,,数列满足,,且是等比数列.
(I)求数列和的通项公式;
(II)求数列的前项和.
20、(本小题满分12分)
从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图:
(I)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的概率;
(II)求频率分布直方图中的的值;
(Ⅲ)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的100名学生该周课外阅读时间的平均数在第几组(只需写出结论).
21、(本小题满分12分)
设分别是椭圆C:的左,右焦点, 是C上一点,且与轴垂直,直线与的另一个交点为。
(I)若直线的斜率为,求C的离心率;
(II)若直线在轴上的截距为2且||=5||,求.
22、(本小题满分12分)
设.
(Ⅰ)令,求 的单调区间;
(Ⅱ)已知在处取得极大值.求实数的取值范围.
文科数学参考答案
一、 选择题
(1) B (2)B (3)D (4)A (5)A (6)C
(7) C (8)B (9)D (10)C (11)D (12)A
二、 填空题
(13) (14)1 (15)8 (16)
三、 解答题
(17) 解:(1) (2)
(18) 解:
(I)
(II)
(19) 解:⑴ 设等差数列的公差为,由题意得
所以.
设等比数列的公比为,由题意得,解得.
所以.从而
⑵ 由⑴知.数列的前项和为,
数列的前项和为.
所以,数列的前项和为.
20解:(Ⅰ)根据频数分布表,100名学生中课外阅读时间不少于12小时的学生共有名,所以样本中的学生课外阅读时间少于12小时的频率是.
从该校随机选取一名学生,估计其课外阅读时间少于12小时的概率为.
(Ⅱ)课外阅读时间落在组的有17人,频率为,所以.
课外阅读时间落在组的有25人,频率为,所以.
(Ⅲ)样本中的100名学生课外阅读时间的平均数在第4组
21.
(I)
(II) ①
带入 ②
将①及带入②得
22解:(Ⅰ)由
可得,
则,
当时,
时,,函数单调递增;
当时,
时,,函数单调递增,
时,,函数单调递减.
所以当时,函数单调递增区间为;
当时,函数单调递增区间为,单调递减区间为.
(Ⅱ)由(Ⅰ)知,.
①当时,,单调递减.
所以当时,,单调递减.
当时,,单调递增.
所以在x=1处取得极小值,不合题意.
②当时,,由(Ⅰ)知在内单调递增,
可得当当时,,时,,
所以在(0,1)内单调递减,在内单调递增,
所以在x=1处取得极小值,不合题意.
③当时,即时,在(0,1)内单调递增,在 内单调递减,
所以当时,, 单调递减,不合题意.
④当时,即 ,当时,,单调递增,
当时,,单调递减,
所以f(x)在x=1处取得极大值,合题意.
综上可知,实数a的取值范围为.