甘肃省镇原县二中2018-2019学年高二上学期期末考试数学（理）试卷 16页

‎2018—2019学年度第一学期期末考试试题 高二（数学）（理）‎ 一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．)‎ ‎1．命题“a∉A或b∉B”的否定形式是(　　)‎ A．若a∉A，则b∉B B．a∈A或b∈B C．a∉A且b∉B D．a∈A且b∈B ‎2．已知a∈R，则“a＜2”是“a2＜2a”的(　　)‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎3．若椭圆＋＝1(a＞b＞0)的离心率为，则双曲线－＝1的离心率为(　　) A.　　　B.　　　C.　　　D. ‎4．若a＝(0,1，－1)，b＝(1,1,0)，且(a＋λb)⊥a，则实数λ的值是(　　)‎ A．－1 B．0 C．1 D．－2‎ ‎5．下列说法正确的是(　　)‎ A．“x2＝1”是“x＝1”的充分不必要条件 B．“x＝－1”是“x2－5x－6＝0”的必要不充分条件 C．命题“∃x0∈R，使得x＋x0＋1＜0”的否定是：“∀x∈R，均有x2＋x＋1＜0”‎ D．命题“若α＝β，则sin α＝sin β”的逆否命题为真命题 ‎6．平面直角坐标系xOy中，若定点A(1,2)与动点P(x，y)满足·＝4，则点P的轨迹方程是(　　)‎ A．x＋y＝4 B．2x＋y＝4 C．x＋2y＝4 D．x＋2y＝1‎ ‎7．如图1，在正方体ABCD—A1B1C1D1中，M、N分别为A1B1、CC1的中点，P为AD上一动点，记α为异面直线PM与D1N所成的角，则α的集合是(　　)‎ A. B. C. D. 图1‎ ‎8．已知圆x2＋y2＋mx－＝0与抛物线y＝x2的准线相切，则m＝(　　)‎ A．±2 B. C. D．± ‎9．给出两个命题：p：|x|＝x的充要条件是x为正实数，q：不等式|x－y|≤|x|＋|y|取等号的条件是xy＜0，则下列命题是真命题的是(　　)‎ A．p∧q B．p∨q C．(p)∧q D．(p)∨q ‎10．直线y＝x－3与抛物线y2＝4x交于A、B两点，过A、B 两点向抛物线的准线作垂线，垂足为P、Q，则梯形APQB的面积为(　　)‎ A．48 B．56 C．64 D．72‎ ‎11．若点O和点F分别为椭圆＋＝1的中心和左焦点，点P为椭圆上的任意一点，则·的最大值为(　　)‎ A．2 B．3 C．6 D．8‎ ‎12．已知抛物线x2＝2py(p＞0)的焦点为F，过F作倾斜角为30°的直线，与抛物线交于A，B两点，若∈(0,1)，则＝(　　)‎ A. B. C. D. 二、填空题(本大题共4小题，每小题5分，共20分．)‎ ‎13．已知双曲线－＝1的右焦点为(，0)，则该双曲线的渐近线方程为________．‎ ‎14．已知a，b是两个命题，如果a是b的充分条件，那么“a”是“b”的________条件．‎ ‎15．已知正方体ABCD—A1B1C1D1，P、M为空间任意两点，如果有＝＋6＋7＋4，那么M点一定在平面________内．‎ ‎16．已知F是双曲线－＝1(a＞0，b＞0)的左焦点，E是双曲线的右顶点，过点F且垂直于x轴的直线与双曲线交于A，B两点，若△ABE是锐角三角形，则该双曲线的离心率e的取值范围为________．‎ 三、解答题(本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤．)‎ ‎17．(本小题满分10分)已知p：2x2－9x＋a＜0，q：且q是p的必要条件，求实数a的取值范围．‎ ‎18．(本小题满分12分)如图3，四边形MNPQ是圆C的内接等腰梯形，向量与的夹角为120°，·＝2.‎ ‎(1)建立坐标系，求圆C的方程；‎ ‎(2)求以M，N为焦点，过点P，Q的椭圆方程．‎ 图3‎ ‎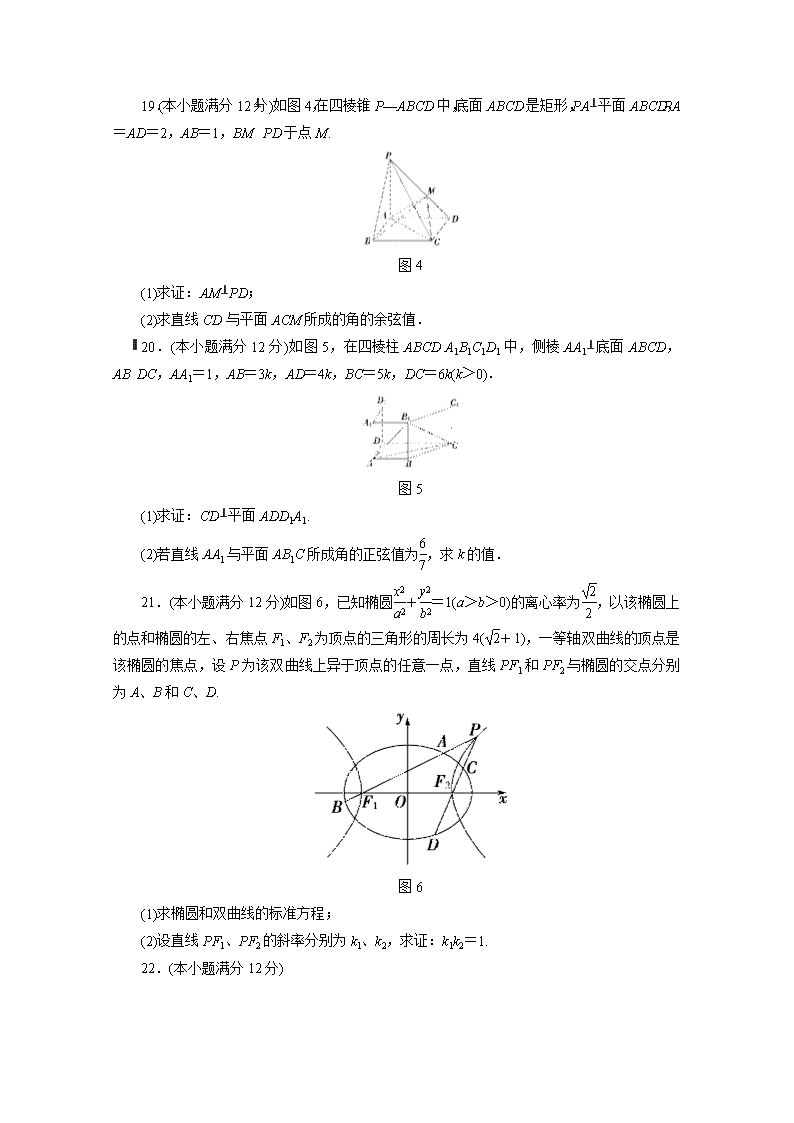19．(本小题满分12分)如图4，在四棱锥P—ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA＝AD＝2，AB＝1，BM⊥PD于点M.‎ 图4‎ ‎(1)求证：AM⊥PD；‎ ‎(2)求直线CD与平面ACM所成的角的余弦值．‎ ‎20．(本小题满分12分)如图5，在四棱柱ABCDA1B1C1D1中，侧棱AA1⊥底面ABCD，AB∥DC，AA1＝1，AB＝3k，AD＝4k，BC＝5k，DC＝6k(k＞0)．‎ 图5‎ ‎(1)求证：CD⊥平面ADD1A1.‎ ‎(2)若直线AA1与平面AB1C所成角的正弦值为，求k的值．‎ ‎21．(本小题满分12分)如图6，已知椭圆＋＝1(a＞b＞0)的离心率为，以该椭圆上的点和椭圆的左、右焦点F1、F2为顶点的三角形的周长为4(＋1)，一等轴双曲线的顶点是该椭圆的焦点，设P为该双曲线上异于顶点的任意一点，直线PF1和PF2与椭圆的交点分别为A、B和C、D.‎ 图6‎ ‎(1)求椭圆和双曲线的标准方程；‎ ‎(2)设直线PF1、PF2的斜率分别为k1、k2，求证：k1k2＝1.‎ ‎22．(本小题满分12分)‎ 图7‎ 如图，点P(0，－1)是椭圆C1：＋＝1(a＞b＞0)的一个顶点，C1的长轴是圆C2：x2＋y2＝4的直径．l1，l2是过点P且互相垂直的两条直线，其中l1交圆C2于A，B两点，l2交椭圆C1于另一点D.‎ ‎(1)求椭圆C1的方程；‎ ‎(2)求△ABD面积取最大值时直线l1的方程．‎ 镇原二中高二数学上学期期末数学试题（理）‎ ‎(时间：120分钟，满分：150分)‎ 一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．)‎ ‎1．命题“a∉A或b∉B”的否定形式是(　　)‎ A．若a∉A，则b∉B　　　 B．a∈A或b∈B C．a∉A且b∉B D．a∈A且b∈B ‎【解析】　“p或q”的否定为“非p且非q”，D正确．‎ ‎【答案】　D ‎2．已知a∈R，则“a＜2”是“a2＜2a”的(　　)‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎【解析】　∵a2＜2a⇔a(a－2)＜0⇔0＜a＜2.‎ ‎∴“a＜2”是“a2＜2a”的必要不充分条件．‎ ‎【答案】　B ‎3．若椭圆＋＝1(a＞b＞0)的离心率为，则双曲线－＝1的离心率为(　　)‎ A.　　　B.　　　C.　　　D. ‎【解析】　由题意，1－＝2＝，∴＝，而双曲线的离心率e2＝1＋＝1＋＝，∴e＝.‎ ‎【答案】　B ‎4．若a＝(0,1，－1)，b＝(1,1,0)，且(a＋λb)⊥a，则实数λ的值是(　　)‎ A．－1 B．0 ‎ C．1 D．－2‎ ‎【解析】　∵a＋λb＝(0,1，－1)＋(λ，λ，0)＝(λ，1＋λ，－1)‎ ‎∵(a＋λb)⊥a，∴(a＋λb)·a＝1＋λ＋1＝0，∴λ＝－2.‎ ‎【答案】　D ‎5．下列说法正确的是(　　)‎ A．“x2＝1”是“x＝1”的充分不必要条件 B．“x＝－1”是“x2－5x－6＝0”的必要不充分条件 C．命题“∃x0∈R，使得x＋x0＋1＜0”的否定是：“∀x∈R，均有x2＋x＋1＜0”‎ D．命题“若α＝β，则sin α＝sin β”的逆否命题为真命题 ‎【解析】　“x2＝1”是“x＝1”的必要不充分条件，“x＝－1”是“x2－5x－6＝0”的充分不必要条件，A、B均不正确；C中命题的否定应该为“∀x∈R，均有x2＋x＋1≥0”，故C不正确．‎ ‎【答案】　D ‎6．平面直角坐标系xOy中，若定点A(1,2)与动点P(x，y)满足·＝4，则点P的轨迹方程是(　　)‎ A．x＋y＝4 B．2x＋y＝4‎ C．x＋2y＝4 D．x＋2y＝1‎ ‎【解析】　由＝(x，y)，＝(1,2)得·＝(x，y)·(1,2)＝x＋2y＝4，x＋2y＝4即为所求轨迹方程，故选C.‎ ‎【答案】　C ‎7．如图1，在正方体ABCD—A1B1C1D1中，M、N分别为A1B1、CC1的中点，P为AD上一动点，记α为异面直线PM与D1N所成的角，则α的集合是(　　)‎ 图1‎ A. B. C. D. ‎【解析】　分别以DA、DC、DD1所在的直线为x、y、z轴，D 为原点建系，连结AM、DM，可以证明⊥，⊥，故D1N⊥平面ADM，∴D1N⊥PM，即α＝.‎ ‎【答案】　A ‎8．已知圆x2＋y2＋mx－＝0与抛物线y＝x2的准线相切，则m＝(　　)‎ A．±2 B. ‎ C. D．± ‎【解析】　抛物线方程可化为x2＝4y，∴其准线方程为y＝－1，圆的方程可化为2＋y2＝＋，是以为圆心.为半径的圆，由题意知＝1，∴m＝±.‎ ‎【答案】　D ‎9．给出两个命题：p：|x|＝x的充要条件是x为正实数，q：不等式|x－y|≤|x|＋|y|取等号的条件是xy＜0，则下列命题是真命题的是(　　)‎ A．p∧q B．p∨q C．(p)∧q D．(p)∨q ‎【解析】　命题p为假，因为x＝0时，也有|x|＝x成立；命题q也为假，因为当x＝0或y＝0时，|x－y|≤|x|＋|y|也成立，因此只有(p)∨q为真命题．‎ ‎【答案】　D ‎10．直线y＝x－3与抛物线y2＝4x交于A、B两点，过A、B两点向抛物线的准线作垂线，垂足为P、Q，则梯形APQB的面积为(　　)‎ A．48 B．56 ‎ C．64 D．72‎ ‎【解析】　联立可解得A(1，－2)，B(9,6)．‎ ‎∵抛物线准线为x＝－1，∴|AP|＝2，|BQ|＝10，|PQ|＝8，‎ ‎∴S＝＝48.‎ ‎【答案】　A ‎11．若点O和点F分别为椭圆＋＝1的中心和左焦点，点P 为椭圆上的任意一点，则·的最大值为(　　)‎ A．2 B．3 C．6 D．8‎ ‎【解析】　设椭圆上任意一点P(x0，y0)，则有＋＝1，即y＝3－x，O(0,0)，F(－1,0)，‎ 则·＝x0(x0＋1)＋y＝x＋x0＋3‎ ‎＝(x0＋2)2＋2.‎ ‎∵|x0|≤2，∴当x0＝2时，·取得最大值为6.‎ ‎【答案】　C ‎12．已知抛物线x2＝2py(p＞0)的焦点为F，过F作倾斜角为30°的直线，与抛物线交于A，B两点，若∈(0,1)，则＝(　　)‎ A. B. C. D. ‎【解析】　因为抛物线的焦点为，直线方程为y＝x＋，与抛物线方程联立得x2－px－p2＝0，解方程得xA＝－p，xB＝p，所以＝＝.故选C.‎ ‎【答案】　C 二、填空题(本大题共4小题，每小题5分，共20分．)‎ ‎13．已知双曲线－＝1的右焦点为(，0)，则该双曲线的渐近线方程为________．‎ ‎【解析】　由题意得：9＋a＝13，∴a＝4，故渐近线方程为y＝±x.‎ ‎【答案】　y＝±x ‎14．已知a，b是两个命题，如果a是b的充分条件，那么“a”是“b”‎ 的________条件．‎ ‎【解析】　由题意a⇒b成立，故其逆否命题为b⇒a也成立．‎ ‎∴“a”是“b”的必要条件．‎ ‎【答案】　必要 ‎15．已知正方体ABCD—A1B1C1D1，P、M为空间任意两点，如果有＝＋6＋7＋4，那么M点一定在平面________内．‎ ‎【解析】　∵＝－＝＋6＋6＋4 ‎＝＋6＋4 ‎＝＋2＋4，‎ ‎∴－＝2＋4，‎ 即＝2＋4.‎ 故，，共面，即M点在平面A1BCD1内．‎ ‎【答案】　A1BCD1‎ ‎16．已知F是双曲线－＝1(a＞0，b＞0)的左焦点，E是双曲线的右顶点，过点F且垂直于x轴的直线与双曲线交于A，B两点，若△ABE是锐角三角形，则该双曲线的离心率e的取值范围为________．‎ ‎【解析】　∵△ABE为等腰三角形，可知只需∠AEF＜45°即可，即|AF|＜|EF|⇒＜a＋c，化简得e2－e－2＜0，又e＞1，∴1＜e＜2，∴该双曲线的离心率e的取值范围为(1,2)．‎ ‎【答案】　(1,2)‎ 三、解答题(本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤．)‎ ‎17．(本小题满分10分)已知p：2x2－9x＋a＜0，q：且q是p的必要条件，求实数a的取值范围．‎ ‎【解】　由 得即2＜x＜3.‎ ‎∴q：2＜x＜3.‎ 设A＝{x|2x2－9x＋a＜0}，B＝{x|2＜x＜3}，‎ ‎∵p⇒q，∴q⇒p.‎ ‎∴BA.‎ 即2＜x＜3满足不等式2x2－9x＋a＜0.设f(x)＝2x2－9x＋a，‎ 要使2＜x＜3满足不等式2x2－9x＋a＜0，‎ 需即 ‎∴a≤9.故所求实数a的取值范围是{a|a≤9}．‎ ‎18．(本小题满分12分)如图3，四边形MNPQ是圆C的内接等腰梯形，向量与的夹角为120°，·＝2.‎ ‎(1)建立坐标系，求圆C的方程；‎ ‎(2)求以M，N为焦点，过点P，Q的椭圆方程．‎ 图3‎ ‎【解】　(1)建立如图坐标系，由题意得：△CQM为正三角形．‎ ‎∴·＝r2·cos 60°＝2，∴r＝2，‎ ‎∴圆C的方程为：x2＋y2＝4.‎ ‎(2)M(2,0)，N(－2,0)，Q(1，)，2a＝|QN|＋|QM|＝2＋2.‎ ‎∴c＝2，a＝＋1，b2＝a2－c2＝2.‎ ‎∴椭圆方程为：＋＝1.‎ ‎19．(本小题满分12分)如图4，在四棱锥P—ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA＝AD＝2，AB＝1，BM⊥PD于点M.‎ 图4‎ ‎(1)求证：AM⊥PD；‎ ‎(2)求直线CD与平面ACM所成的角的余弦值．‎ ‎【解】　(1)证明　∵PA⊥平面ABCD，AB⊆平面ABCD，‎ ‎∴PA⊥AB.‎ ‎∵AB⊥AD，AD∩PA＝A，‎ ‎∴AB⊥平面PAD.‎ ‎∵PD⊂平面PAD，‎ ‎∴AB⊥PD.‎ ‎∵BM⊥PD，AB∩BM＝B，‎ ‎∴PD⊥平面ABM.‎ ‎∵AM⊂平面ABM，∴AM⊥PD.‎ ‎(2)如图所示，以点A为坐标原点，建立空间直角坐标系Axyz，则A(0,0,0)，P(0,0,2)，B(1,0,0)，C(1,2,0)，D(0,2,0)，M(0,1,1)，‎ 于是＝(1,2,0)，＝(0,1,1)，＝(－1,0,0)．‎ 设平面ACM的一个法向量为n＝(x，y，z)，‎ 由n⊥，n⊥可得 令z＝1，得x＝2，y＝－1，于是n＝(2，－1,1)．‎ 设直线CD与平面ACM所成的角为α，‎ 则sin α＝＝，cos α＝.‎ 故直线CD与平面ACM所成的角的余弦值为.‎ ‎20．(本小题满分12分)如图5，在四棱柱ABCDA1B1C1D1中，侧棱AA1⊥底面ABCD，AB∥DC，AA1＝1，AB＝3k，AD＝4k，BC＝5k，DC＝6k(k＞0)．‎ 图5‎ ‎(1)求证：CD⊥平面ADD1A1.‎ ‎(2)若直线AA1与平面AB1C所成角的正弦值为，求k的值．‎ 图(1)‎ ‎【证明】　(1)取CD的中点E，连结BE，如图(1)．‎ ‎∵AB∥DE，AB＝DE＝3k，‎ ‎∴四边形ABED为平行四边形，‎ ‎∴BE∥AD且BE＝AD＝4k.‎ 在△BCE中，∵BE＝4k，CE＝3k，‎ BC＝5k，‎ ‎∴BE2＋CE2＝BC2，‎ ‎∴∠BEC＝90°，即BE⊥CD.‎ 又∵BE∥AD，∴CD⊥AD.‎ ‎∵AA1⊥平面ABCD，CD⊂平面ABCD，‎ ‎∴AA1⊥CD.‎ 又AA1∩AD＝A，∴CD⊥平面ADD1A1.‎ 图(2)‎ ‎(2)以D为原点，，，的方向为x，y，z轴的正方向建立如图(2)所示的空间直角坐标系，则A(4k,0,0)，C(0,6k,0)，B1(4k,3k,1)，A1(4k,0,1)，‎ ‎∴＝(－4k,6k,0)，＝(0,3k,1)，＝(0,0,1)．‎ 设平面AB1C的法向量n＝(x，y，z)，则由得 取y＝2，得n＝(3,2，－6k)．‎ 设AA1与平面AB1C所成的角为θ，则 sin θ＝|cos〈，n〉|＝＝＝，解得k＝1，故所求k的值为1.‎ ‎21．如图6，已知椭圆＋＝1(a＞b＞0)的离心率为，以该椭圆上的点和椭圆的左、右焦点F1、F2为顶点的三角形的周长为4(＋1)，一等轴双曲线的顶点是该椭圆的焦点，设P为该双曲线上异于顶点的任意一点，直线PF1和PF2与椭圆的交点分别为A、B和C、D.‎ 图6‎ ‎(1)求椭圆和双曲线的标准方程；‎ ‎(2)设直线PF1、PF2的斜率分别为k1、k2，求证：k1k2＝1.‎ ‎【解】　(1)设椭圆的半焦距为c，由题意知＝，2a＋2c＝4(＋1)，所以a＝2，c＝2.‎ 又a2＝b2＋c2，因此b＝2.‎ 故椭圆的标准方程为＋＝1.‎ 由题意设等轴双曲线的标准方程为－＝1(m＞0)，因为等轴双曲线的顶点是椭圆的焦点，所以m＝2，‎ 因此双曲线的标准方程为－＝1.‎ ‎(2)设P(x0，y0)，则k1＝，k2＝.‎ 因为点P在双曲线x2－y2＝4上，所以x－y＝4.‎ 因此k1k2＝·＝＝1，即k1k2＝1.‎ ‎22．(本小题满分12分)‎ 图7‎ 如图，点P(0，－1)是椭圆C1：＋＝1(a＞b＞0)的一个顶点，C1的长轴是圆C2：x2＋y2＝4的直径．l1，l2是过点P且互相垂直的两条直线，其中l1交圆C2于A，B两点，l2交椭圆C1于另一点D.‎ ‎(1)求椭圆C1的方程；‎ ‎(2)求△ABD面积取最大值时直线l1的方程．‎ ‎【解】　(1)由题意得 所以椭圆C的方程为＋y2＝1.‎ ‎(2)设A(x1，y1)，B(x2，y2)，D(x0，y0)．由题意知直线l1的斜率存在，不妨设其为k，则直线l1的方程为y＝kx－1.‎ 又圆C2：x2＋y2＝4，故点O到直线l1的距离d＝，‎ 所以|AB|＝2＝2.‎ 又l2⊥l1，故直线l2的方程为x＋ky＋k＝0.‎ 由消去y，‎ 整理得(4＋k2)x2＋8kx＝0，‎ 故x0＝－，所以|PD|＝.‎ 设△ABD的面积为S，则S＝|AB|·|PD|＝，‎ 所以S＝≤＝，当且仅当k＝±时取等号．‎ 所以所求直线l1的方程为y＝±x－1.‎