- 595.42 KB
- 2021-04-14 发布
山大附中2019~2020学年第一学期期中考试
高二年级数学试题(文)
考试时间:90分钟 满分:100分
一.选择题:(本题有12个小题,每小题3分,共36分)
1.直线的倾斜角大小是( )
A. B. C. D.
2.如图,平行四边形是水平放置的一个平面图形的直观图,其中,
,,则下列叙述正确的是( )
A.原图形是正方形 B.原图形是非正方形的菱形
C.原图形的面积是 D.原图形的面积是
3.已知,,则直线不通过( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
4.设为直线,是两个不同的平面,下列命题中正确的是( )
A.若,,则 B.若,,则
C.若,,则 D.若,,则
5.点,,直线与线段相交,则实数的取值范围是( )
A.或 B.
C. D.或
6.如图,在四面体中,点分别是棱的中点,
截面是正方形,则下列结论错误的为( )
A. B. 截面
C. D.异面直线与所成的角为45°
7.已知点,,若直线过原点,且、两点
到直线的距离相等, 则直线的方程为( )
A. 或 B.或
C.或 D. 或
8.在直三棱柱中,,,则点到平面 的距离为( )
A. B. C. D.
9.用一块圆心角为、半径为的扇形铁皮制成一个无底面的圆锥容器(接缝忽略不计),则该容器的体积为( )
A. B. C. D.
10.当点到直线的距离最大时,的值为( )
A.3 B.0 C. D.1
11.正方体中,分别是棱和上的点,
,那么正方体中过的截面图形是( )
A.三角形 B.四边形 C.五边形 D.六边形
12.如图,在棱长为的正方体中,为的中点,为
上任意一点,为上任意两点,且的长为定值,则下面四个值
中不为定值的是( )
A.点到平面的距离
B.直线与平面所成的角
C.三棱锥的体积
D.二面角的大小
二.填空题:(本题有5个小题,每小题4分,共20分)
13.圆台的两个底面面积之比为,母线与底面的夹角是,轴截面的面积为,则圆台的侧面积为 .
14. 正三棱柱的底面边长为2,高为2,则它的外接球表面积为 .
15.空间中点关于轴的对称点,点,则连线的长度为 .
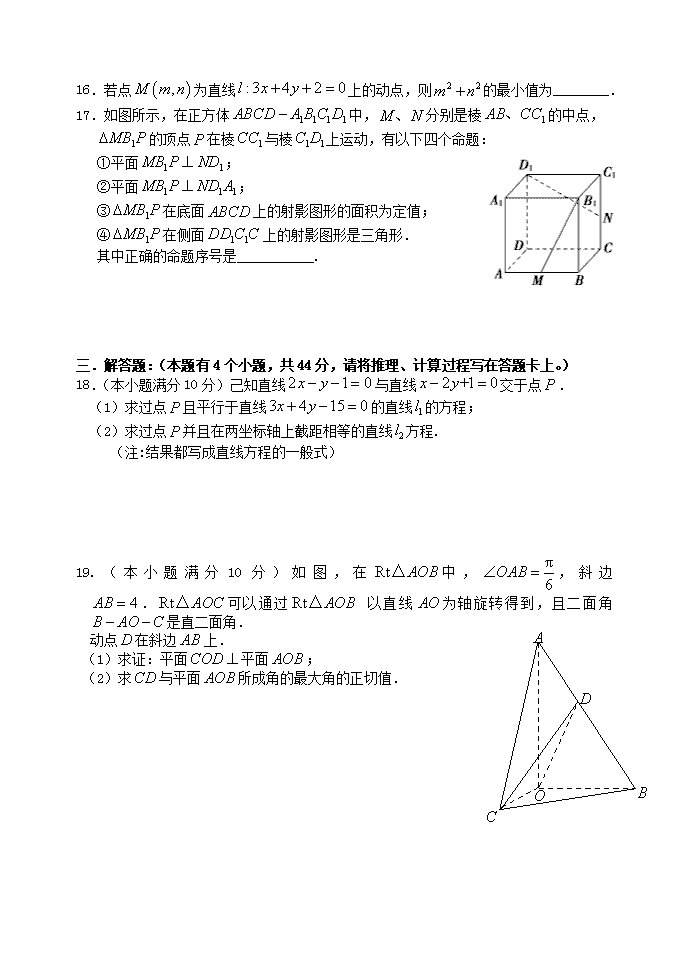
16.若点为直线上的动点,则的最小值为________.
17.如图所示,在正方体中,分别是棱的中点,
的顶点在棱与棱上运动,有以下四个命题:
①平面;
②平面;
③在底面上的射影图形的面积为定值;
④在侧面上的射影图形是三角形.
其中正确的命题序号是___________.
三.解答题:(本题有4个小题,共44分,请将推理、计算过程写在答题卡上。)
18.(本小题满分10分)己知直线与直线交于点.
(1)求过点且平行于直线的直线的方程;
(2)求过点并且在两坐标轴上截距相等的直线方程.
(注:结果都写成直线方程的一般式)
19. (本小题满分10分)如图,在中,,斜边.可以通过 以直线为轴旋转得到,且二面角是直二面角.
动点在斜边上.
(1)求证:平面平面;
(2)求与平面所成角的最大角的正切值.
20.(本小题满分12分)
在如图所示的空间几何体中,平面平面, 与是边长为的等边三角形,,和平面所成的角为,且点在平面上的射影落在的平分线上.
(1)求证:平面;
(2)求三棱锥体的体积.
21.(本小题满分12分)如图1,四棱锥中,底面,面
是直角梯形,为侧棱上一点.该四棱锥的俯视图和侧(左)视图如图2所示.
(1)证明:平面;
(2)线段上是否存在点,使与所成角的余弦值为?若存在,
找到所有符合要求的点,并求的长;若不存在,说明理由.
山大附中2019~2020学年第一学期期中考试
高二年级数学试题(文)评分细则
考试时间:90分钟 满分:100分
一、选择题(3×12=36分)
1
2
3
4
5
6
7
8
9
10
11
12
D
C
C
B
A
A
D
B
A
C
C
B
二、填空题(4×5=20分)
13. 14. 15. 16. 17. ②③
三.解答题(满分44分,解答应写出文字说明,证明过程或演算步骤)
18. (本小题满分10分)己知直线与直线交于点.
(1)求过点且平行于直线的直线的方程;
(2)求过点并且在两坐标轴上截距相等的直线方程.
(注:结果都写成直线方程的一般式)
18.解:
联立,解得,得点. ……………1分
(1)设平行于直线的直线的方程为,
把代入可得:解得. ……………3分
∴过点且平行于直线的直线的方程为.
……………4分
(2)当直线经过原点时,可得方程为:. ……………6分
当直线不过原点时,可设方程为:把代入可得可得
……………8分
∴直线的方程为 ……………9分
综上可得:直线的方程为或 ……………10分
19.(本小题满分10分)
如图,在中,,斜边.可以通过 以直线为轴旋转得到,且二面角是直二面角.动点在斜边上.
(1)求证:平面平面;
(2)求与平面所成角的最大角的正切值.
19.解:(1)证明:由题意,
∴是二面角的平面角, ……………1分
又二面角是直二面角,
∴, ……………2分
又∵,
∴平面。 ……………4分
(2)解:由(1)知,平面,
∴是与平面所成的角, ……………5分
且, ……………6分
当最小时,最大, ……………7分
这时,,垂足为, ……………9分
∴与平面所成的角最时的正切值为. ……………10分
20. (本小题满分12分)
在如图所示的空间几何体中,平面平面,与是边长为的等边三角形,,和平面所成的角为,且点在平面上的射影落在的平分线上.
(1)求证:平面;
(2)求二面角的余弦值.
20.(本小题满分12分)
解:(1)由题意知,,都是边长为2的等边三角形,取中点,连接,则,, ……………………2分
又∵平面⊥平面,∴⊥平面,作⊥平面,
那么,根据题意,点落在上,
∴,易求得,…………4分
∴四边形是平行四边形,∴,∴平面 ………6分
(2)因为,平面平面,平面,
平面平面
所以平面,即平面, …………7分
由(1)知,
故. …………9分
又, …………10分
. …………11分
…………12分
21.(本小题满分12分)
如图1,四棱锥中,底面,面是直角梯形,为侧棱上一点.该四棱锥的俯视图和侧(左)视图如图2所示.
(1)证明:平面;
(2)线段上是否存在点,使与所成角的余弦值为?若存在,找到所有符合要求的点,并求的长;若不存在,说明理由.
21.解:(1)证明:由俯视图可得,,
所以. …………2分
又因为 平面,
所以 , …………3分
所以 平面. …………4分
(2)解:线段上存在点,使与所成角的余弦值为.
证明如下:
因为 平面,,所以两两垂直,建立如图所示的空间直角坐标系.
…………5分
所以 .
设 ,其中. …………6分
所以,. …………7分
要使与所成角的余弦值为,则有 , …………9分
所以 ,解得 或, …………11分
均适合.
故点位于点处,此时;或中点处,此时,有与所成角的余弦值为. …………12分