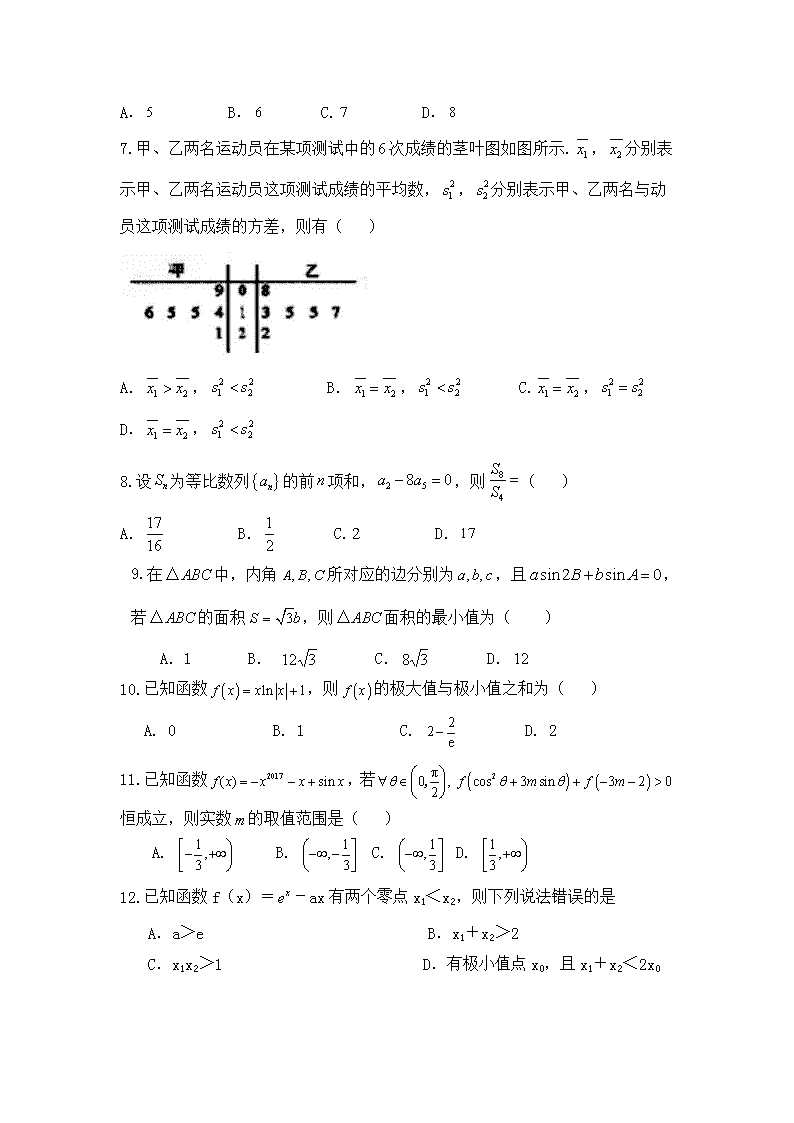2017-2018学年陕西省黄陵中学高二（重点班）下学期开学考试数学（文）试题 Word版 10页

‎2017-2018学年陕西省黄陵中学高二（重点班）下学期开学考试数学试题（文）‎ 一、选择题（本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.）‎ ‎1.抛物线的焦点坐标是（ ）‎ A． B．‎ C． D．‎ ‎2. 命题“，”的否定是（ ）‎ A．， B．，‎ C．， D．，‎ ‎3. 下列命题中，不是真命题的是（ ）‎ A．命题“若，则”的逆命题.‎ B．“”是“且”的必要条件.‎ C．命题“若，则”的否命题.‎ D．“”是“”的充分不必要条件. ‎ ‎4. 某工厂的三个车间在12月份共生产了3600双皮靴，在出厂前要检查这批产品的质量，决定采用分层抽样的方法进行抽取，若从一、二、三车间抽取的产品数分别为、、，且，则第二车间生产的产品数为（ ）‎ A．800 B．‎1000 C．1200 D．1500‎ ‎5.下列命题中，说法错误的是（ ）‎ A．“若，则”的否命题是“若，则” ‎ B.“是真命题”是 “是真命题”的充分不必要条件 ‎ C.“，”的否定是“，” ‎ D．“若，则是偶函数”的逆命题是真命题 ‎6.设，，若是与的等比中项，则的最小值是（ ）‎ A． B． C. D．‎ ‎7.甲、乙两名运动员在某项测试中的次成绩的茎叶图如图所示.，分别表示甲、乙两名运动员这项测试成绩的平均数，，分别表示甲、乙两名与动员这项测试成绩的方差，则有（ ）‎ A．， B．， C.， D．，‎ ‎8.设为等比数列的前项和，，则（ ）‎ A． B． C. D．‎ ‎9.在中，内角所对应的边分别为，且，若的面积，则面积的最小值为（ ）‎ ‎ A．1 B． C． D． ‎ ‎10.已知函数，则的极大值与极小值之和为（ ） A. 0 B. ‎1 ‎C. D. 2‎ ‎11.已知函数，若恒成立，则实数的取值范围是（ ） A. B. C. D. ‎ ‎12.已知函数f（x）＝－ax有两个零点x1＜x2，则下列说法错误的是 A．a＞e B．x1＋x2＞2‎ C．x1x2＞1 D．有极小值点x0，且x1＋x2＜2x0‎ 二、填空题(本大题共4小题，每小题5分，共20分．请把正确答案填在题中横线上)‎ ‎13.若，，则 ．‎ ‎14. 已知数列的前项和为，则数列的通项公式为 . ‎ ‎15.若不等式的解集为，则不等式的解集为 ．‎ ‎16.已知直线，是之间的一定点，并且点到的距离分别为1，2，是直线上一动点，，与直线交于点，则面积的最小值为 ．‎ 三、解答题(本大题共6个小题，70分。)‎ ‎17. (本题10分)已知函数.‎ ‎（1）求函数的最小值；‎ ‎（2）若对任意的恒成立，求实数的取值范围.‎ ‎18. (本题12分)如图，由围成的曲边三角形，在曲线弧上求一点，使得过所作的的切线与围城的三角形的面积最大，并求得最大值．‎ ‎19. (本题12分)在直三棱柱ABC﹣A1B‎1C1中，AC=3，BC=4，AB=5，AA1=4，点D是AB的中点，‎ ‎（Ⅰ）求证：A‎1C1⊥BC1；‎ ‎（Ⅱ）求证：AC1∥平面CDB1．‎ ‎20. (本题12分)如图,直线与圆 且与椭圆相交于两点.‎ ‎(1)若直线恰好经过椭圆的左顶点,求弦长 ‎(2)设直线的斜率分别为,判断是否为定值,并说明理由 ‎(3)求，面积的最小值.‎ ‎21．已知关于的不等式．‎ ‎（1）若关于的不等式的解集为或，求的值；‎ ‎（2）解关于的不等式.‎ ‎22．已知数列的前项和为，且满足.‎ ‎（1）求数列的通项公式；‎ ‎（2）设，记数列的前项和为，若对任意的，恒成立，求实数的取值范围.‎ ‎1-5: ABACC 6-10:DDABD 11‎‎-12AC ‎13．1； 14．； 15．； 16．2．‎ ‎17.(1) 当时， 取最小值且为;(2) .‎ ‎（1）函数的定义域为 ‎ ‎，‎ 在，‎ 所以当时， 取最小值且为 ‎（2）问题等价于： 对恒成立，‎ 令，则，‎ 因为，所以，‎ 所以在上单调递增，‎ 所以， 所以 ‎ ‎[]‎ ‎18.， .‎ 设 ，则 ，‎ ‎∵ ， ，‎ 即 ∴。 ‎ 令，得 , ∴, ‎ 令，得, ∴. ‎ ‎∴ , ‎ ‎, ‎ 令，则（舍去）或， 即当时， , ‎ ‎∴ ,∴ .‎ ‎19. ‎ 证明(法一: 故有,A. 法二: ;由直三棱柱;;平面; 平面,平面, 平面,‎ ‎(连接相交于点O,连OD,易知// , 平面 , 平面,故//平面.‎ ‎20.‎ ‎（1）由题意直线斜率存在，设直线 因为直线与圆相切，.‎ 所以 解得 当时，由解得，所以 当时，同理 所以。‎ ‎（2）（ⅰ）当直线的斜率不存在时，得；‎ ‎（ⅱ）当的斜率存在时，设直线 ‎ 因为直线与圆相切，‎ 所以 整理得所以①，‎ 由消去y整理得，‎ 由直线与圆相交得 设 则 ，②‎ 所以③，‎ 将①②代入③式得 综上可得 ‎ ‎（3）由（2）知 记直线与圆的切点为 设 所以，‎ 则 所以当时， .‎ ‎21.(1)解：由题，方程的两根分别为，，‎ 于是 解得.‎ ‎（2）原不等式等价于，等价于 ‎①当时，原不等式的解集为；‎ ‎②当时，，，‎ 当时，原不等式的解集为或；‎ 当时，‎ ‎（i）若，即时，原不等式解集为 ‎（ii）若，即时，原不等式解集为 ‎（iii）当，即时，原不等式的解集为.‎ ‎22.（1）当时，，解得 当时，，‎ 化简得，，‎ 所以是以2为首项，2为公比的等比数列，‎ 所以.‎ ‎（2）因为，‎ 所以的前项和 因为对任意，恒成立，‎ 所以，整理得]‎ 因为，‎ 当且仅当时取等号，所以 所以要想对任意，恒成立，‎ 则 所以实数的取值范围是.‎ ‎.‎