2020年中考数学总复习 第4讲 二次根式 新版 新人教版 2页

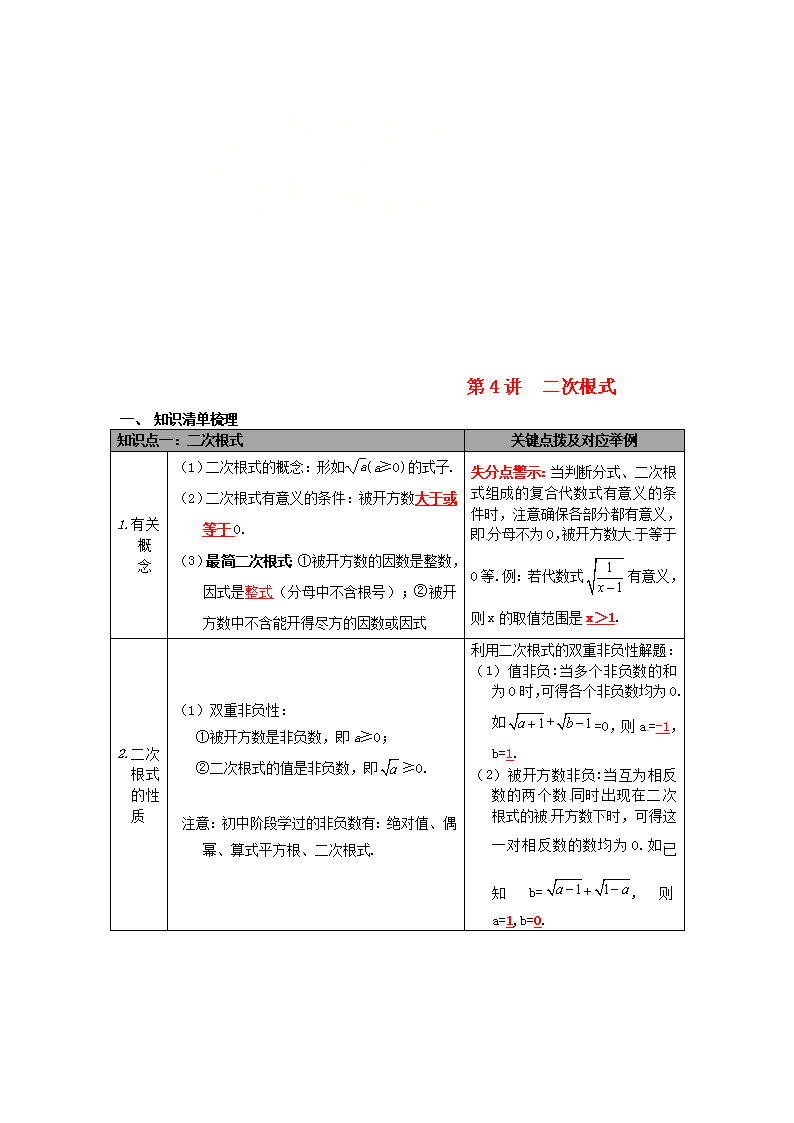
第4讲 二次根式 一、 知识清单梳理 ‎ 知识点一：二次根式 ‎ 关键点拨及对应举例 ‎1.有关概念 ‎（1）二次根式的概念：形如(a≥0)的式子.‎ ‎（2）二次根式有意义的条件：被开方数大于或等于0.‎ ‎（3）最简二次根式：①被开方数的因数是整数，因式是整式（分母中不含根号）；②被开方数中不含能开得尽方的因数或因式 失分点警示：当判断分式、二次根式组成的复合代数式有意义的条件时，注意确保各部分都有意义，即分母不为0，被开方数大于等于0等.例：若代数式有意义，则x的取值范围是x＞1.‎ ‎2.二次根式的性质 ‎（1）双重非负性：‎ ‎①被开方数是非负数，即a≥0；‎ ‎②二次根式的值是非负数，即≥0.‎ 注意：初中阶段学过的非负数有：绝对值、偶幂、算式平方根、二次根式.‎ 利用二次根式的双重非负性解题：‎ ‎（1）值非负:当多个非负数的和为0时，可得各个非负数均为0.如+=0，则a=-1，b=1. ‎ ‎（2）被开方数非负:当互为相反数的两个数同时出现在二次根式的被开方数下时，可得这一对相反数的数均为0.如已知b=+,则a=1,b=0.‎ ‎(2)两个重要性质：‎ ‎①()2＝a(a≥0)；②＝|a|＝；‎ ‎(3)积的算术平方根：＝·(a≥0，b≥0)；‎ ‎(4)商的算术平方根： (a≥0，b＞0)．‎ 例：计算：‎ ‎＝3.14；＝2；‎ ‎=；=2 ；‎ 知识点二 ：二次根式的运算 ‎3.二次根式的加减法 先将各根式化为最简二次根式，再合并被开方数相同的二次根式．‎ 例：计算：＝.‎ ‎4.二次根式的乘除法 ‎（1）乘法：·=(a≥0，b≥0)；‎ ‎（2）除法： = (a≥0，b＞0)．‎ 注意：将运算结果化为最简二次根式.‎ 例：计算：＝1；4.‎ ‎5.二次根式的混合运算 运算顺序与实数的运算顺序相同，先算乘方，再算乘除，最后算加减，有括号的先算括号里面的（或先去括号）．‎ 运算时，注意观察，有时运用乘法公式会使运算简便.‎ 例：计算：(+1)( -1)= 1 .‎ 一、 习题处理 中考一本通P13---6、7 P15---5‎ 三、课后反思：‎