数学理卷·2018届湖北省黄石三中（稳派教育）高三阶段性检测（2017 10页

湖北省黄石市第三中学（稳派教育）2018届高三阶段性检测 理数试卷 第Ⅰ卷（共60分）‎ 一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1.若，，则( )‎ A． B． C． D．‎ ‎2.下列命题正确的是（ ）‎ A．， ‎ B．函数在点处的切线斜率是0 ‎ C．函数的最大值为，无最小值 ‎ D．若，则 ‎3.若把函数的图象向左平移个单位长度后，所得到的图象关于原点对称，则的最小值是（ ）‎ A．1 B．2 C．3 D．4‎ ‎4.已知中，，分别为边上的六等分点.设，则（ ）‎ A．180 B．300 C. 360 D．480‎ ‎5.已知数列是递增的等比数列，且，则（ ）‎ A．6 B．8 C．10 D．12‎ ‎6.已知向量满足，则的最大值是（ ）‎ A．3 B．4 C. 5 D．6‎ ‎7.已知定义在上的奇函数满足，又，且当时，恒成立，则函数的零点的个数为（ ）‎ A．2 B．3 C. 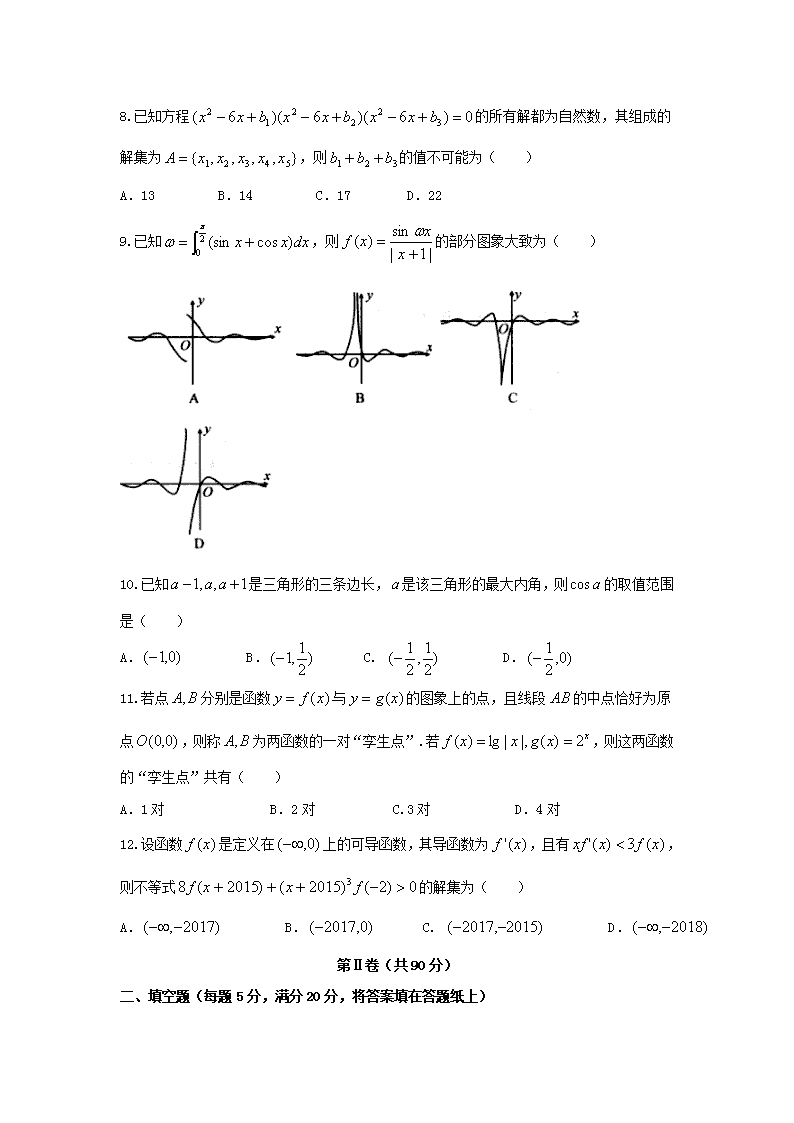4 D．5‎ ‎8.已知方程的所有解都为自然数，其组成的解集为，则的值不可能为（ ）‎ A．13 B．14 C．17 D．22‎ ‎9.已知，则的部分图象大致为（ ）‎ ‎10.已知是三角形的三条边长，是该三角形的最大内角，则的取值范围是（ ）‎ A． B． C. D．‎ ‎11.若点分别是函数与的图象上的点，且线段的中点恰好为原点，则称为两函数的一对“孪生点”.若，则这两函数的“孪生点”共有（ ）‎ A．1对 B．2对 C.3对 D．4对 ‎12.设函数是定义在上的可导函数，其导函数为，且有，则不等式的解集为（ ）‎ A． B． C. D．‎ 第Ⅱ卷（共90分）‎ 二、填空题（每题5分，满分20分，将答案填在答题纸上）‎ ‎13.我国古代数学著作《九章算术》有“今有金箠，长五尺，斩本一尺，重四斤，斩末一尺，重二斤，问次一尺各重几何？”意思是：“现有一根金箠，一头粗，一头细，在粗的一端截下1尺，重4斤；在细的一端截下1尺，重2斤；问依次每一尺各重多少斤？”根据上题的已知条件，若金箠由粗到细是依次等量减小的，则正中间一尺的重量为 ．‎ ‎14.分别以边长为1的正方形的顶点为圆心，1为半径作圆弧，交于点，则曲边三角形的周长为 . ‎ ‎15.下表给出一个“三角形数阵”：‎ ‎，‎ ‎，，‎ ‎……‎ 已知每一列的数成等差数列；从第三行起，每一行的数成等比数列，每一行的公比都相等.记第行第列的数为，则（1） ；（2）前20行中这个数共出现了 次．‎ ‎16.已知是外接圆的圆心，若且，则 ．‎ ‎(的角所对边分别为，外接圆半径为，有)‎ 三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） ‎ ‎19.在锐角中，.‎ ‎（1）若的面积等于，求；‎ ‎（2）求的面积的取值范围. ‎ ‎18.设数列的前项和为，且.令.‎ ‎（1）求的通项公式；‎ ‎（2）若，且数列的前项和为，求.‎ ‎19.某校高二（1）班学生为了筹措经费给班上购买课外读物，班委会成立了一个社会实践小组，决定利用暑假八月份（30天计算）轮流换班去销售一种时令水果.在这30天内每斤水果的收入（元）与时间（天）的部分数据如下表所示，已知日销售（斤）与时间（天）满足一次函数关系.‎ ‎（1）根据提供的图象和表格，下厨每斤水果的收入（元）与时间（天）所满足的函数关系式及日销售量（斤）与时间（天）的一次函数关系； ‎ ‎（2）用（元）表示销售水果的日收入，写出与的函数关系式，并求这30天中第几天日收入最大，最大值为多少元？‎ ‎20.已知，分别为等差数列和等比数列，，的前项和为.函数的导函数是，有，且是函数的零点.‎ ‎（1）求的值；‎ ‎（2）若数列公差为，且点，当时所有点都在指数函数的图象上.‎ 请你求出解析式，并证明：.‎ ‎21.如图，已知，分别是中点，弧 的半径分别为，点平分弧，过点作弧的切线分别交于点.四边形为矩形，其中点在线段上，点在弧上，延长与交于点.设，矩形的面积为.‎ ‎（1）求的解析式并求其定义域；‎ ‎（2）求的最大值.‎ ‎22.设函数.‎ ‎（1）当时，求的单调区间；‎ ‎（2）若的图象与轴交于两点，起，求的取值范围；‎ ‎（3）在（2）的条件下，求证.‎ ‎（参考知识：若，则有）‎ 试卷答案 一、选择题 ‎1-5：BCACD 6-10：CBACB 11、12：BC 二、填空题 ‎13．3斤 14． 15．（1）；（2）4 16．‎ 三、解答题 ‎17、解：(1)∵，由正弦定理得，‎ ‎∵，∴，得.‎ 由得，‎ 所以由解得.‎ ‎（2）由正弦定理得，‎ ‎∴.‎ 又，∴.‎ 因为为锐角三角形，∴，‎ ‎∴.‎ ‎18.（1）当时，得 ‎∴.‎ ‎∵，∴（）.‎ ‎（2），‎ 所以 作差得，‎ ‎∴.‎ ‎19、（1）依题意可设，当时，线段过点，得；‎ 当时，线段过点，得.‎ 所以.‎ 令，由表中数据得，所以.‎ ‎（2）由得 当时，在上的单调递增，在 上单调递减，所以当时，有最大值为元；当时，在上单调递减，所以.‎ 综合上述得：在第十天时日收入最大，最大值为90元.‎ ‎20、解：（1）由得，又，所以 ‎∴.‎ ‎∵的零点为，而是的零点，又是等比数列的首项，所以，，‎ ‎∴.‎ ‎（2）∵，‎ 令的公比为，则.‎ 又都在指数函数的图象上，即，即当时恒成立，‎ 解得.所以.‎ ‎∵，‎ 因为，所以当时，有最小值为，所以.‎ ‎21、（1）∵，又，‎ ‎∴，由圆的性质得是中点.‎ 依题意得弧的半径分别为2,1‎ 在中，，，∴，，‎ ‎∴.‎ ‎∵，平分，所以为等腰直角三角形，‎ ‎∴，∴即 ‎∴，又为锐角，∴.‎ 所以的定义域为.‎ ‎（2）因为 令，‎ ‎∵，∴，则在上单调递增，‎ ‎∴，‎ ‎∴，∴在上单调递增，‎ ‎∴.‎ ‎22、（1）当时，得，解得，‎ ‎∴函数的单调递增区间为，单调减区间为.‎ ‎（2），依题意可知，此时得，‎ 在上单调递减，在上单调递增，又或时，‎ ‎，‎ ‎∴的图象与轴交于两点，‎ 当且仅当即 得.‎ ‎∴的取值范围为.‎ ‎（3）由题意得得，‎ 欲证即证即证，‎ 即.‎ ‎∴，得证.‎ ‎ ‎