- 948.50 KB
- 2021-04-13 发布
四川省泸县第五中学2018-2019学年高二下学期期末模拟
文科数学试题
第I卷(共60分)
一.选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,有且只有一项是符合题目要求的. 请将其编号选出,并涂在机读卡上的相应位置)
1.是虚数单位,计算的结果为
A. B. C. D.
2. 已知,,则
A. B. C. D.
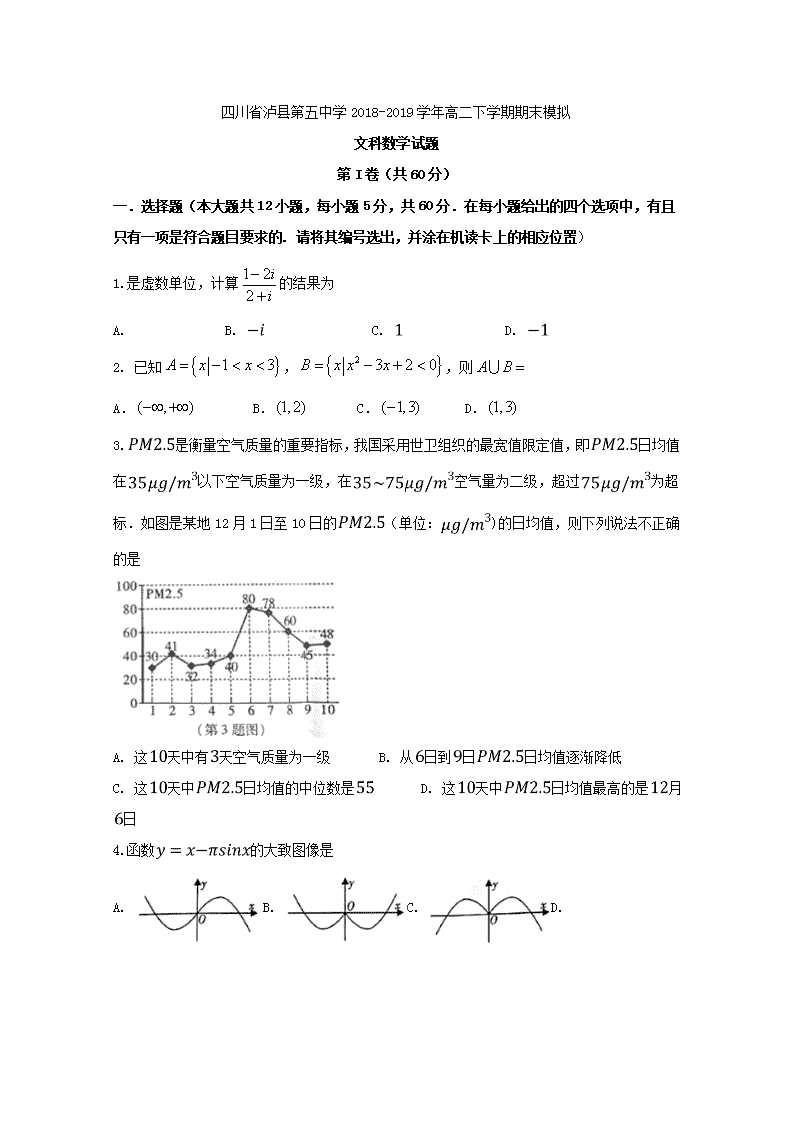
3.是衡量空气质量的重要指标,我国采用世卫组织的最宽值限定值,即日均值在以下空气质量为一级,在空气量为二级,超过为超标.如图是某地12月1日至10日的(单位:)的日均值,则下列说法不正确的是
A. 这天中有天空气质量为一级 B. 从日到日日均值逐渐降低
C. 这天中日均值的中位数是 D. 这天中日均值最高的是月日
4.函数的大致图像是
A. B. C. D.
5.已知,在区间上任取一个实数,则的概率为
A. B. C. D.6.过双曲线的一个焦点作实轴的垂线,交双曲线于,两点,若线段的长度恰等于焦距,则双曲线的离心率为
A. B. C. D.
7.老师带甲乙丙丁四名学生去参加自主招生考试,考试结束后老师向四名学生了解考试情况,四名学生回答如下:甲说:“我们四人都没考好”;乙说:“我们四人中有人考的好”;丙说:“乙和丁至少有一人没考好”;丁说:“我没考好”.结果,四名学生中有两人说对了,则四名学生中说对两人是.
A. 甲 丙 B. 乙 丁 C. 丙 丁 D. 乙 丙
8.已知,,,则、、的大小关系是
A. B. C. D.
9.已知函数,则的极大值点为
A. B. C. D.
10.中,,,将沿上的高折成直二面角,则三棱锥的外接球的表面积为
A. B. C. D.
11.已知定义在上的函数的导函数为,任意,有,且,设,,
,则
A. B.
C. D.
12.已知函数 对任意 都存在 使得 则 的最大值为
A. B. C. D.
第Ⅱ卷(共90分)
二.填空题(本大题共4小题,每小题5分,共20分)
13.实数满足约束条件,则的最小值是________.
14.一个几何体的三视图如图所示,则该几何体的体积为__.
15.已知,,且,则的最小值为_______.
16.关于的不等式的解集为,则实数的取值范围是___________。
三.解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17.(12分)2018年中央电视台春节联欢晚会分会场之一落户黔东南州黎平县肇兴侗寨,黔东南州某中学高二社会实践小组就社区群众春晚节目的关注度进行了调查,
随机抽取80名群众进行调查,将他们的年龄分成6段:,,,,,,得到如图所示的频率分布直方图.问:
(Ⅰ)求这80名群众年龄的中位数;
(Ⅱ)若用分层抽样的方法从年龄在中的群众随机抽取6名,并从这6名群众中选派3人外出宣传黔东南,求选派的3名群众年龄在的概率.
18.(12分).设函数,.
(1)当(为自然对数的底数)时,求的极小值;
(2)若在上为单调增函数,求的取值范围.
19.(12分)一只药用昆虫的产卵数与一定范围内与温度有关, 现收集了该种药用昆虫的6组观测数据如下表:
温度/℃
21
23
24
27
29
32
产卵数/个
6
11
20
27
57
77
(1)若用线性回归模型,求关于的回归方程=x+(精确到0.1);
(2)若用非线性回归模型求关的回归方程为 且相关指数
( i )试与 (1)中的线性回归模型相比,用 说明哪种模型的拟合效果更好.
( ii )用拟合效果好的模型预测温度为时该种药用昆虫的产卵数(结果取整数).
附:一组数据(x1,y1), (x2,y2), ...,(xn,yn), 其回归直线=x+的斜率和截距的最小二乘估计为,,相关指数.
。
20.(12分)设定点,动点满足:以为直径的圆与轴相切.
(I)求动点的轨迹的方程;
(Ⅱ)设,是曲线上两点,若曲线在点,处的切线互相乖直,求证:,,三点共线.
21.(12分)已知.
(1)讨论的单调性;
(2)有三个不同的零点,求的取值范围.
请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题记分,作答时请写清题号.
22.(选修4-4:坐标系与参数方程)(10分)
以坐标原点为极点,轴正半轴为极轴建立极坐标系,曲线的极坐标方程是.
(1)求曲线的直角坐标方程;
(2)设过点且倾斜角为的直线和曲线交于两点,,求的值.
23.[选修4-5:不等式选讲]
已知函数,且的解集为.
(1)求实数的值;
(2)设,, ,且,求的最大值.
2019年春四川省泸县第五中学高二期末模拟考试
文科数学试题答案
一.选择题
1.B 2.C 3.C 4.D 5.B 6.C 7.D 8.D 9.D 10.C
11.A 12.A
二.填空题
13. 14. 15. 16.
三解答题
17.解(Ⅰ)设80名群众年龄的中位数为,则
,解得,
即80名群众年龄的中位数55.
(Ⅱ)由已知得,年龄在中的群众有人,
年龄在的群众有人, 按分层抽样的方法随机抽取年龄在的群众
人,记为1,2;随机抽取年龄在的群众人, 记为.则基本事件有:
,
共20个,参加座谈的导游中有3名群众年龄都在的基本事件有:共4个,设事件为“从这6名群众中选派3人外出宣传黔东南,选派的3名群众年龄都在”,则
18.(1)由题设,当时,,则,()
∴当,,在上单调递减,
当,,在上单调递增,
∴当时,取得极小值,,∴的极小值为2.
(2)因为在上为单调增函数,
所以对于恒成立,
即对于恒成立,
进而
19.(1)由题意得, ,
,,
所以,
∴33−6.626=−138.6,
∴y关于x的线性回归方程为=6.6x−138.6.
(2) ( i )由所给数据求得的线性回归方程为=6.6x−138.6,
又,
故得相关指数为,
因为0.9398<0.9522,
所以回归方程 比线性回归方程=6.6x−138.6拟合效果更好.
( ii )由( i )得当x= C时,.
即当温度x=35℃时,该种药用昆虫的产卵数估计为190个.
20.(I)设,则的中点为,依题意知到点与它到轴相等,
可得,
化简得,即为动点的轨迹的方程.
(II)设,,则由得,
知曲线在点,处的切线的斜率分别是,,
依题意,即,可得,
,,
,知,,三点共线.
21.(1)由已知的定乂域为,又,
当时,恒成立;
当时,令得;令得.
综上所述,当时,在上为增函数;
当时,在上为增函数,在上为减函数.
(2)由题意,则,
当时,∵,
∴在上为增函数,不符合题意.
当时,,
令,则.
令的两根分别为且,
则∵,∴,
当时,,∴,∴在上为增函数;
当时,,∴,∴在上为减函数;
当时,,∴,∴在上为增函数.
∵,∴在上只有一个零点 1,且。
∴
,
,
.
∵,又当时,.∴
∴在上必有一个零点.
∴
.
∵,又当时,,∴.
∴在上必有一个零点.
综上所述,故的取值范围为.
22.(1)由得,将代入得,
即为曲线的直角坐标方程.
(2)依题意得直线(为参数),与椭圆联立得
.
即,可得,, .
,
23.(1)依题意得,即,
可得.
(2)依题意得()由柯西不等式得,
,
当且仅当,即,,时取等号.
,,,
的最大值为