四川省棠湖中学2020届高三数学（理）第二次高考适应性试题（Word版附答案） 14页

1 四川省棠湖中学高 2020 届第二次高考适应性考试 理科数学 注意事项： 1．答卷前，考生务必将自己的姓名和准考证号填写在答题卡上。 2．回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑。如需改动，用橡 皮擦干净后，再选涂其它答案标号。回答非选择题时，将答案写在答题卡上。写在本试卷上无效。3．考 试结束后，将本试卷和答题卡一并交回。 第 I 卷 选择题（60 分） 一、选择题：本题共 12 小题，每小题 5 分，共 60 分。在每小题给的四个选项中，只有一项是符合 题目要求的。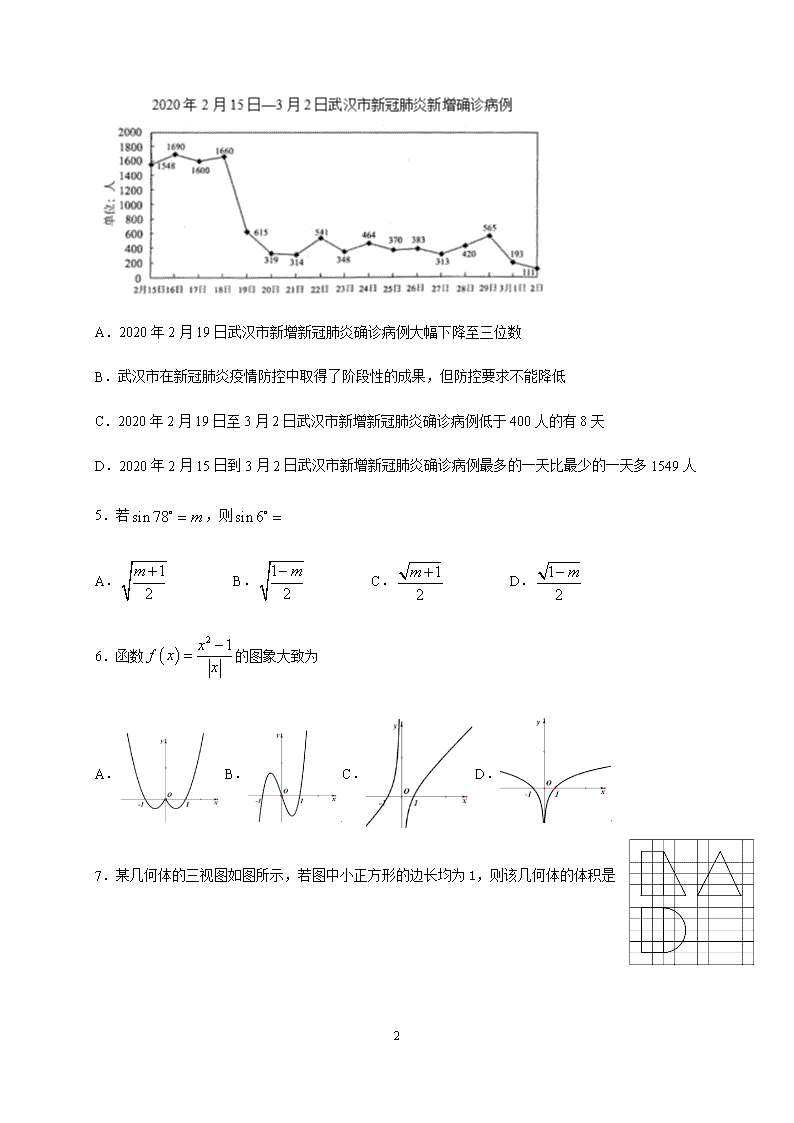 1． z 是 z 的共轭复数，若  2, 2(z z z z i i    为虚数单位) ，则 z = A．1 i B． 1 i  C． 1 i  D．1 i 2．集合  2| 2 3 0x x xA    ，集合  2| 1,B y y x x R    ，则 R A B ð A．[ 1,1] B． ( 1,1) C．[ 1.3] D． ( 1.3) 3．已知实数 x 、 y 满足不等式组 2 1 0 2 1 0 0 x y x y y          ，则 3z x y   的最大值为 A．3 B． 2 C． 3 2  D． 2 4．下图是 2020 年 2 月 15 日至 3 月 2 日武汉市新增新冠肺炎确诊病例的折线统计图．则下列说法不 正确的是 2 A．2020 年 2 月 19 日武汉市新增新冠肺炎确诊病例大幅下降至三位数 B．武汉市在新冠肺炎疫情防控中取得了阶段性的成果，但防控要求不能降低 C．2020 年 2 月 19 日至 3 月 2 日武汉市新增新冠肺炎确诊病例低于 400 人的有 8 天 D．2020 年 2 月 15 日到 3 月 2 日武汉市新增新冠肺炎确诊病例最多的一天比最少的一天多 1549 人 5．若sin 78 m ，则sin 6  A． 1 2 m  B． 1 2 m C． 1 2 m  D． 1 2 m 6．函数   2 1xf x x  的图象大致为 A． B． C． D． 7．某几何体的三视图如图所示，若图中小正方形的边长均为 1，则该几何体的体积是 3 A． 1616 3  B． 816 3  C． 32 8 3 3  D． 32 16 3 3  8．已知等差数列{ }na 的前 n 项和为 ,nS 9 12 2 1 6, 4,2a a a   则数列 1{ } nS 的前 10 项和为 A． 11 12 B．10 11 C． 9 10 D． 8 9 9．将函数   sin2f x x 的图象向左平移 0 2       个单位长度，得到的函数为偶函数，则 的 值为 A． 12  B． 6  C． 3  D． 4  10．从装有若干个大小相同的红球、白球和黄球的袋中随机摸出 1 个球，摸到红球、白球和黄球的 概率分别为 1 1 1, ,2 3 6 ，从袋中随机摸出一个球，记下颜色后放回，连续摸 3 次，则记下的颜色中有红 有白，但没有黄的概率为 A． 5 36 B． 5 6 C． 5 12 D． 1 2 11．已知抛物线 2 4y x 的焦点为 F ，准线与 x 轴的交点为 K ，点 P 为抛物线上任意一点 KPF 的 平分线与 x 轴交于 ( ,0)m ，则 m 的最大值为 A．3 2 2 B． 2 3 3 C． 2 3 D． 2 2 12．设函数 ( ) ( )(ln )x mf x e ax x ax   ，若存在实数 a 使得 ( ) 0f x  恒成立，则 m 的取值范围是 A． ,0 B． 0,2 C． 2  ， D． ,2 第 II 卷 非选择题（90 分） 4 二、填空题：本题共 4 小题，每小题 5 分，共 20 分。 13．曲线 ( ) xf x xe 在点 (1, (1))f 处的切线在 y 轴上的截距是_______. 14．在 3 2( )nx x  的二项展开式中，所有项的系数之和为 81，则常数项为________ 15．双曲线 2 2 2 2 1x y a b   的左右焦点分别为 1F 、 2F ， P 是双曲线右支上一点， I 为 1 2PF F 的内心， PI 交 x 轴于Q 点，若 1 2FQ PF ，且 : 2:1PI IQ  ，则双曲线的离心率 e 的值为__________． 16．在三棱锥 P ABC 中， 60ABC   ， 90PBA PCA    o ， 3PB PC  ，点 P 到底面 ABC 的距离为 2 ，则三棱锥 P ABC 的外接球的表面积为________. 三．解答题：共 70 分。解答应写出文字说明、证明过程或演算步骤。第 17~21 题为必考题，每个试 题考生都必须作答。第 22、23 题为选考题，考生根据要求作答。 （一）必考题：共 60 分 17．（12 分）某校的一个社会实践调查小组，在对该校学生的良好“用眼习惯”的调查中，随机发 放了 120 分问卷.对收回的 100 份有效问卷进行统计，得到如 2 2 下列联表： 做不到科学用眼 能做到科学用眼 合计 男 45 10 55 女 30 15 45 合计 75 25 100 （1）现按女生是否能做到科学用眼进行分层，从 45 份女生问卷中抽取了 6 份问卷，从这 6 份问卷 中再随机抽取 3 份，并记其中能做到科学用眼的问卷的份数 X ，试求随机变量 X 的分布列和数学 期望； （2）若在犯错误的概率不超过 P 的前提下认为良好“用眼习惯”与性别有关，那么根据临界值表， 5 最精确的 P 的值应为多少？请说明理由. 附：独立性检验统计量        2 2 n ad bcK a b c d a c b d      ，其中 n a b c d    . 独立性检验临界值表：  2 0P K k 0.25 0.15 0.10 0.05 0.025 0k 1.323 2.072 2.706 3.840 5.024 18．（12 分）已知数列 na 是等差数列，前 n 项和为 nS ，且 5 33S a ， 4 6 8a a  ． （1）求 na ． （2）设 2n n nb a  ，求数列 nb 的前 n 项和 nT ． 19．（12 分）如图，几何体是圆柱的一部分，它是由矩形 ABCD(及其内部)以 AB 边所在直线为旋转 轴旋转 120°得到的，G 是 DF 的中点. (1)设 P 是 CE 上的一点，且 AP⊥BE，求∠CBP 的大小； (2)当 AB＝3，AD＝2 时，求二面角 E－AG－C 的大小. 20．（12 分）已知抛物线 2 2y px （ 0p  ）上的两个动点  1 1,A x y 和  2 2,B x y ，焦点为 F.线段 AB 的中点为  03,M y ，且 A，B 两点到抛物线的焦点 F 的距离之和为 8. 6 （1）求抛物线的标准方程； （2）若线段 AB 的垂直平分线与 x 轴交于点 C，求 ABC 面积的最大值. 21．（12 分）已知 ( ) ln( 1) .axf x e x x   （1）若 a=1，且 f(x)≥m 在(0，+∞)恒成立，求实数 m 的取值范围； （2）当 1 2a  时，若 x=0 不是 f(x)的极值点，求实数 a 的取值. （二）选考题：共 10 分。请考生在第 22、23 题中任选一题作答。如果多做，则按所做的第一题计 分。 22．[选修 4-4：坐标系与参数方程]（10 分） 在平面直角坐标系 xOy 中，曲线 C 的参数方程为 1 cos sin x y       （ 为参数），以坐标原点为极点， x 轴的正半轴为极轴建立极坐标系，直线 l 的极坐标方程为 sin 2 24       . （1）求曲线 C 的极坐标方程和直线 l 的直角坐标方程； （2）若射线 0 2         与曲线 C 交于点 A（不同于极点 O），与直线 l 交于点 B，求 | | | | OA OB 的最大值. 23．[选修 4-5：不等式选讲]（10 分） 设函数 ( ) 2 1 1f x x x    .  1 画出 ( )y f x 的图像；  2 若 ( )f x m x n  ，求 m n 的最小值. 7 8 四川省棠湖中学高 2020 届第二次高考适应性考试 理科数学参考答案 1．D 2．A 3．A 4．D 5．B 6．D 7．B 8．B 9．D 10．C 11．A 12．D 13． e 14．8 15． 3 2 16． 6 17．（1）“科学用眼”抽 人，“不科学用眼”抽 人．则随机变量 ， ∴ ， ， 分布列为 0 1 2 （2） 由表可知 2．706＜3．030＜3．840；∴ ． 18．(1)由题意，数列 na 是等差数列，所以 5 35S a ，又 5 33S a ， 3 0a  ， 由 4 6 58 2a a a   ，得 5 4a  ，所以 5 3 2 4a a d   ，解得 2d  ， 所以数列的通项公式为    3 3 2 3na a n d n     ． 9 (2)由（1）得   12 3 2n n n nb a n      ，      2 3 4 12 2 1 2 0 2 3 2n nT n             ，        3 4 1 22 2 1 2 4 2 32 2n n nT n n              ， 两式相减得    2 3 4 1 22 2 2 2 2 2 3 2n n n nT T n           ，  1 2 28 1 2 8 ( 3) 2 ( 4) 2 161 2 n n nn n             ，即 2( 4) 2 16n nT n     ． 19．(1)因为 AP⊥BE，AB⊥BE，AB，AP ⊂ 平面 ABP，AB∩AP＝A，所以 BE⊥平面 ABP. 又 BP ⊂ 平面 ABP，所以 BE⊥BP.又∠EBC＝120°，所以∠CBP＝30°. (2)方法一：如图，取 EC  的中点 H，连接 EH，GH，CH. 因为∠EBC＝120°，所以四边形 BEHC 为菱形， 所以 AE＝GE＝AC＝GC＝ 2 23 2 13  . 取 AG 的中点 M，连接 EM，CM，EC， 则 EM⊥AG，CM⊥AG， 所以∠EMC 为所求二面角的平面角． 又 AM＝1，所以 EM＝CM＝ 13 1 2 3  . 在△BEC 中，由于∠EBC＝120°， 由余弦定理得 EC2＝22＋22－2×2×2×cos 120°＝12， 10 所以 EC＝2 3 ，所以△EMC 为等边三角形， 故所求的角为 60°. 方法二：以 B 为坐标原点，分别以 BE，BP，BA 所在的直线为 x，y，z 轴，建立如图所示的空间直角 坐标系 B－xyz. 由题意得 A(0,0,3)，E(2,0,0)，G(1， 3 ，3)，C(－1， 3 ，0)， 故 AE  ＝(2,0，－3)， AG  ＝(1， 3 ，0)，CG  ＝(2,0,3)． 设 m  ＝(x1，y1，z1)是平面 AEG 的一个法向量， 由 0 0 m AE m AG         可得 1 1 1 1 2 3 0 3 0 x z x y     取 z1＝2，可得平面 AEG 的一个法向量 m  ＝(3，－ 3 ，2)． 设 n  ＝(x2，y2，z2)是平面 ACG 的一个法向量．由 0 0 n AG n CG         可得 2 2 2 2 3 0 2 3 0 x y x z      取 z2＝－2，可得平面 ACG 的一个法向量 n＝(3，－ 3 ，－2)．所以 cos〈 ,m n   〉＝ | || | m n m n     ＝ 1 2 . 故所求的角为 60°. 20．（1）由题意知 1 2 6x x  ，则 1 2| | | | 6 8AF BF x x p p       ，∴ 2p  ， ∴抛物线的标准方程为 2 4y x ； （2）设直线 :AB x my n  （ 0m  ）由 2 4 x my n y x     ，得 2 4 4 0y my n   ， ∴ 1 2 4y y m  ，∴  1 2 1 22 4 22 6x yx y mn nm      ，即 23 2n m  ， 11 即  2 1 2 2 1 2 16 3 0 4 8 12 m y y m y y m            ，∴ 2 2 2 1 2| | 1 4 1 3AB m y y m m        ， 设 AB 的中垂线方程为： 2 ( 3)y m m x    ，即 ( 5)y m x   ，得点 C 的坐标为 (5,0) ， ∵直线 2: 3 2AB x my m   ，即 22 3 0x my m    ， ∴点 C 到直线 AB 的距离 2 2 5 2 3 1 m d m     22 1m  ， ∴  2 21 | | 4 1 32S AB d m m      令 23t m  ，则 2 23 (0 3)m t t    ，  24 4S t t    令  2( ) 4 4f t t t   ，∴  2( ) 4 4 3f t t   ， 令 ( ) 0f t  ，则 2 3 3t  ，在 2 30, 3       上 ( ) 0f t  ；在 2 3 , 33       上 ( ) 0f t  ， 故 ( )f t 在 2 30, 3       单调递增， 2 3 , 33       单调递减， ∴当 2 3 3t  ，即 15 3m   时， max 64 3 9S  . 21．解:（1）由题,当 1a  时,    ln 1xf x e x x   ,所以     1ln 1 11 xf x e x x         , 设      1ln 1 01g x x xx     ,所以    2 0 1 xg x x     恒成立, 所以  g x 在 0,  上为增函数,所以    0 1g x g  ,又 e 1x  , 所以   0f x  恒成立,所以  f x 在 0,  上为增函数,所以    0 0f x f  ,所以 0m  12 （2）       1ln 1 1 ln 1 11 1 ax ax axef x ae x e a xx x              , 令    g x f x ,则       2 2 2 2 1ln 1 1 ax ax ag x e a x x           , 设       2 2 2 2 1ln 1 1 ax ah x a x x      , 则         22 3 3 1 1 12 2 2 01 1 1 a xa ax ah x x x x               , 所以  h x 在 1,  上递增,且  0 2 1h a  , ①当 1 2a  时,  0 0h  ,所以当  1,0x  时,   0h x  ；当  0,x  时,   0h x  , 即当  1,0x  时,   0g x  ；当  0,x  时,   0g x  , 所以    g x f x 在 1,0 上递减,在 0,  上递增,所以    0 0f x f   , 所以  f x 在 1,  上递增,所以 0x  不是  f x 的极值点,所以 1 2a  时,满足条件； ②当 1 2a  时,  0 2 1 0h a   ,又因为  h x 在 1,  上递增, 所以 0 0x  ,使得  0 0h x  ,所以当 0x x 时,   0h x  ,即   0g x  , 所以    g x f x 在 0,x  上递增,又  0 0f   , 所以当 0 0x x  时,   0f x  ；当 0x  时,   0f x  ,所以 0x  是  f x 的极小值点,不合题意, 综上, 1 2a  22．（1）消去参数 可得曲线C 的普通方程是 2 2( 1) 1x y   ，即 2 2 2 0x y x   ，代入 13 cos sin x y        得 2 2 cos   ，即 2cos  ，∴曲线C 的极坐标方程是 2cos  ； 由 sin( ) 2 24     ，化为直角坐标方程为 4x y  ． （2）设 1 2( , ), ( , )B    ，则 1 2cos  ， 2 2 2 sin( )4     ， 1 2 cos sin( )4 2 OA OB       2sin cos cos 1 1 1sin 2 cos22 4 4 4         2 1sin(2 )4 4 4    ， 当 8   时， OA OB 取得最大值为1 2 4  ． 23．（1）由题意，根据绝对值的定义，可得分段函数   3 , 1 12, 1 2 13 , 2 x x f x x x x x              ， 所以 ( )y f x 的图象如图所示： 14 （2）由  f x m x n  ，可得  0f n ，解得 2n  ， 又因为    2 1| ( ) 31f x x x x    ，所以 3m x n x  .(※) 若 3m  ，(※)式明显成立； 若 3m  ，则当 3 nx m   时，(※)式不成立， 由图可知，当 3m  ，且 2n  时，可得   f x m x n  ， 所以当且仅当 3m  ，且 2n  时，   f x m x n  成立， 因此 m n 的最小值为5.