- 682.00 KB
- 2021-04-13 发布
广东仲元中学2016学年第一学期期末考试
高二年级数学(文科)试卷
一、选择题:本大题共12个小题;每小题5分,共60分.在每小题给出的四个选项中,有且只有一项是符合题目要求的.
1.集合,则等于 ( )
A. B. C. D.
2.曲线在点处的切线方程是 ( )
A. B. C. D.
3. 下列函数中,满足“”的单调递增函数是 ( )
A. B. C. D.
4.以下四个命题中,其中真命题的个数为 ( )
①从匀速传递的产品生产流水线上,质检员每10分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;
②对于命题p: ,使得.则,均匀
③“x<0”是 “ln(x+1)<0”的充分不必要条件;
④“若,则,互为相反数”的逆命题
A.1 B.2 C.3 D.4
5.若直线被圆C:截得的弦最短,则直线的方程是( )
A. B. C. D.
6.已知等比数列中,各项都是正数,且成等差数列,则( )
A. B. C. D.
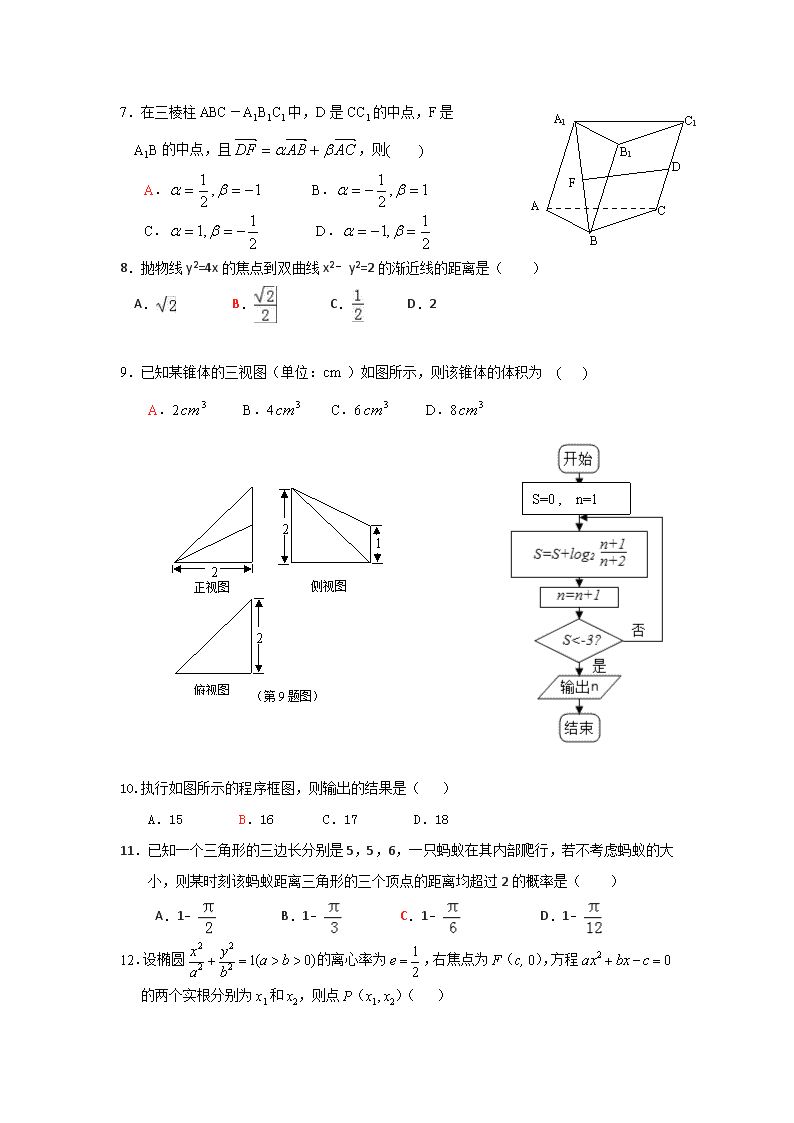
B1
A1
C
B
A
C1
D
F
7.在三棱柱ABC-A1B1C1中,D是CC1的中点,F是
A1B的中点,且,则( )
A. B.
C. D.
8.抛物线y2=4x的焦点到双曲线x2﹣y2=2的渐近线的距离是( )
A. B. C. D.2
9.已知某锥体的三视图(单位:cm )如图所示,则该锥体的体积为 ( )
S=0 , n=1
A.2 B.4 C.6 D.8
(第9题图)
正视图
侧视图
俯视图
2
2
2
1
10.执行如图所示的程序框图,则输出的结果是( )
A.15 B.16 C.17 D.18
11.已知一个三角形的三边长分别是5,5,6,一只蚂蚁在其内部爬行,若不考虑蚂蚁的大小,则某时刻该蚂蚁距离三角形的三个顶点的距离均超过2的概率是( )
A.1﹣ B.1﹣ C.1﹣ D.1﹣
12.设椭圆的离心率为,右焦点为F(c, 0),方程的两个实根分别为x1和x2,则点P(x1, x2)( )
A.必在圆内 B.必在圆上
C.必在圆外 D.以上三种情形都有可能
二、填空题:本大题共5小题,每小题5分,共25分,把答案写在答题卡相应位置上
13.已知向量的夹角为,且,,则 .
14.已知样本7,5,x,3,4的平均数是5,则此样本的方差为 . .
15.球O内有一个内接正方体,正方体的全面积为24,则球O的体积是
16.记不等式组所表示的平面区域为,若直线与有公共点,则的取值范围是 .
三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17. (满分10分) 己知函数的最小正周期为,直线为它的图象的一条对称轴.
(1)求,的值;
(2)在分别为角的对应边,若,=6,求b,c值.
18.(满分12分)某中学对高三年级进行身高统计,测量随机抽取的20名学生的身高,其频率分布直方图如下(单位:cm).
(1)根据频率分布直方图,求出这20名学生身高中位数的估计值和平均数的估计值.
身高(cm)
0.01
0.02
0.03
频率
组距
140
150
160
170
180
0.04
(2)在身高为140~160的学生中任选2个,求至少有一人的身高在150~160之间的概率.
19.(满分12分)已知递增的等差数列中,、是方程的两根,数列为等比数列,
⑴求数列,的通项公式;
⑵记,数列的前项和为.求证:
20. (本小题满分12分)在三棱柱ABC﹣A1B1C1中,△ABC是边长为2的正三角形,侧面BB1C1C是矩形,D、E分别是线段BB1、AC1的中点.
(1)求证:DE∥平面A1B1C1;
(2)若平面ABC⊥平面BB1C1C,BB1=4,求三棱锥A﹣DCE的体积.
21. (本小题满分12分)已知椭圆的中心在坐标原点,离心率,且其中一个焦点与抛物线的焦点重合.
(1)求椭圆的方程;
(2)过点的动直线交椭圆于两点,试问:在坐标平面上是否存在一个定点,使得无论如何转动,以为直径的圆恒过点?若存在,求出点的坐标;若不存在,请说明理由.
【来源:全,品…中&高*考+网】
22. (本小题满分12分)已知函数f(x)=ax+xlnx(a∈R)
(1)当a=2时,求函数f(x)的单调区间。
(2)当a=1且k∈Z时,不等式k(x﹣1)<f(x)在x∈(1,+∞)上恒成立,求k的最大值.
广东仲元中学2016学年第一学期期末考试高二年级数学(文科)参考答案
一、选择题:ADABD CABAB CA
11解:∵三角形的三边长分别是5,5,6,∴三角形的高AD=4,
则三角形ABC的面积S=×6×4=12,
则该蚂蚁距离三角形的三个顶点的距离均超过2,
对应的区域为图中阴影部分,三个小扇形的面积之和为一个
整圆的面积的,圆的半径为2,则阴影部分的面积为S1=12﹣×π×22=12﹣2π,
则根据几何概型的概率公式可得所求是概率为=1﹣,故选:C.
二、填空题:
13. 14. 2 . 15.. 16.
三、解答题
17. (本题满分10分)
解:(Ⅰ)函数的最小正周期为, ……2分
为的图象的一条对称轴,……5分
(Ⅱ),
…………7分
, 即bc=9 。 ……9分
又b+c=6,解得到b=c=3. ……10分
18.(本题满分12分)
解: (1)中位数的左边和右边的直方图的面积相等,由此可以估计中位数的值,
,所以中位数的估计值为162.5.…………………………3分
平均数的估计值等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和.则平均数的估计值为……6分
(2)这20名学生中,身高在140~150之间的有2个,分别为A,B,身高在150~160之间的有6人,分别为C,D,E,F,G,H,则从这8人中任选2个的所有基本事件有
AB,AC,AD,AE,AF,AG,AH,BC,BD,BE,BF,BG,BH,CD,
CE,CF,CG,CH,DE,DF,DG,DH,EF,EG,EH,FG,FH,GH共28个,
两个身高都在140~150之间的事件有AB共1个,
所以至少有一个人在150~160之间的概率为.………………………12分
19. (本题满分12分)
⑴解得, ,因为是递增,所以,……1分
解 得,所以 ……2分
又由, ,得q=, ……4分
所以 。 ……6分
⑵ …………………………7分
……8分
……9分
两式相减得:, ……10分
所以……12分
20. (本题满分12分)
(1)证明:取棱A1C1的中点F,连接EF、B1F…
则由EF是△AA1C1的中位线得EF∥AA1,EF=AA1 ……2分
又DB1∥AA1,DB1=AA1 ……2分
所以EF∥DB1,EF=DB1
故四边形DEFB1是平行四边形,从而DE∥B1F…
所以DE∥平面A1B1C1 …………6分
(Ⅱ)解:因为E是AC1的中点,所以VA﹣DCE=VD﹣ACE=…
过A作AH⊥BC于H…
因为平面平面ABC⊥平面BB1C1C,所以AH⊥平面BB1C1C,…
所以== ……10分
所以VA﹣DCE=VD﹣ACE== …………12分
21.(本题满分12分)
解:(1)设椭圆的方程为,离心率,—1分
又抛物线的焦点为,所以, ——3分
椭圆的方程是. ——4分
(2)若直线与轴重合,则以为直径的圆是,若直线垂直于轴,
则以为直径的圆是. ——5分
由解得即两圆相切于点.
因此所求的点如果存在,只能是. ——6分[
当直线不垂直于轴时,可设直线. ——7分
由消去得. ——8分
设,则 ——9分
又因为, ——10分
——11分
,即以为直径的圆恒过点.
故在坐标平面上存在一个定点满足条件. ——12分
22. (本题满分12分)
解:(1)∵a=2,∴f(x)=2x+xlnx,定义域为(0,+∞)。 ……1分
∴f′(x)=3+lnx,由f′(x)〉0得到x〉e-3 ,由f′(x)〈0得到x〈e-3 ………3分
∴函数f(x)=2x+xlnx的增区间为(e-3,+∞),减区间为(0,e-3). ……4分
(2)当x>1时,x﹣1>0,故不等式k(x﹣1)<f(x)⇔k<,
即对任意x>1恒成立. ……5分
令 则, ……6分
令h(x)=x﹣lnx﹣2(x>1),
则在(1,+∞)上单增.
∵h(3)=1﹣ln3<0,h(4)=2﹣ln4>0,
∴存在x0∈(3,4)使h(x0)=0,
即当1<x<x0时,h(x)<0,即g′(x)<0,
当x>x0时,h(x)>0,即g′(x)>0,
∴g(x)在(1,x0)上单减,在(x0,+∞)上单增. ……10分
令h(x0)=x0﹣lnx0﹣2=0,即lnx0=x0﹣2,
=x0∈(3,4), ……11分
∴k<g(x)min=x0且k∈Z,
即kmax=3. ……12分