- 752.54 KB
- 2021-04-13 发布
2019学年度第二学期期末试卷
高 二 数 学(文)
一、 选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知命题:"若,则",则原命题、逆命题、否命题、逆否命题这四个命题中,真命题的个数是( )
A. B. C. D.
2.已知全集,集合,集合,则下列结论中成立的是( )
A. B.
C. D.
3.是成立的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既非充分又非必要条件
4已知命题p:a2≥0(a∈R),命题q:函数f(x)=x2-x在区间[0,+∞)上单调递增,则下列命题中为真命题的是( )
A.p∨q
B.p∧q
C.(┐p)∧(┐q)
D.(┐p)∨q
5设,不等式的解集是,则等于( )
A.
B.
C.
D.
6.设,则“”是“复数为纯虚数”的( )
A.充分必要条件 B.必要不充分条件
C.充分不必要条件 D.既不充分也不必要条件
7.命题“能被2整除的整数是偶数”的否定( )
A.所有不能被2整除的整数都是偶数
B.所有能被2整除的整数都不是偶数
C.存在一个不能被2整除的整数是偶数
D.存在一个能被2整除的整数不是偶数
8.如图,已知是实数集,集合则阴影部分表示的集合是( )
- 9 -
A.
B.
C.
D.
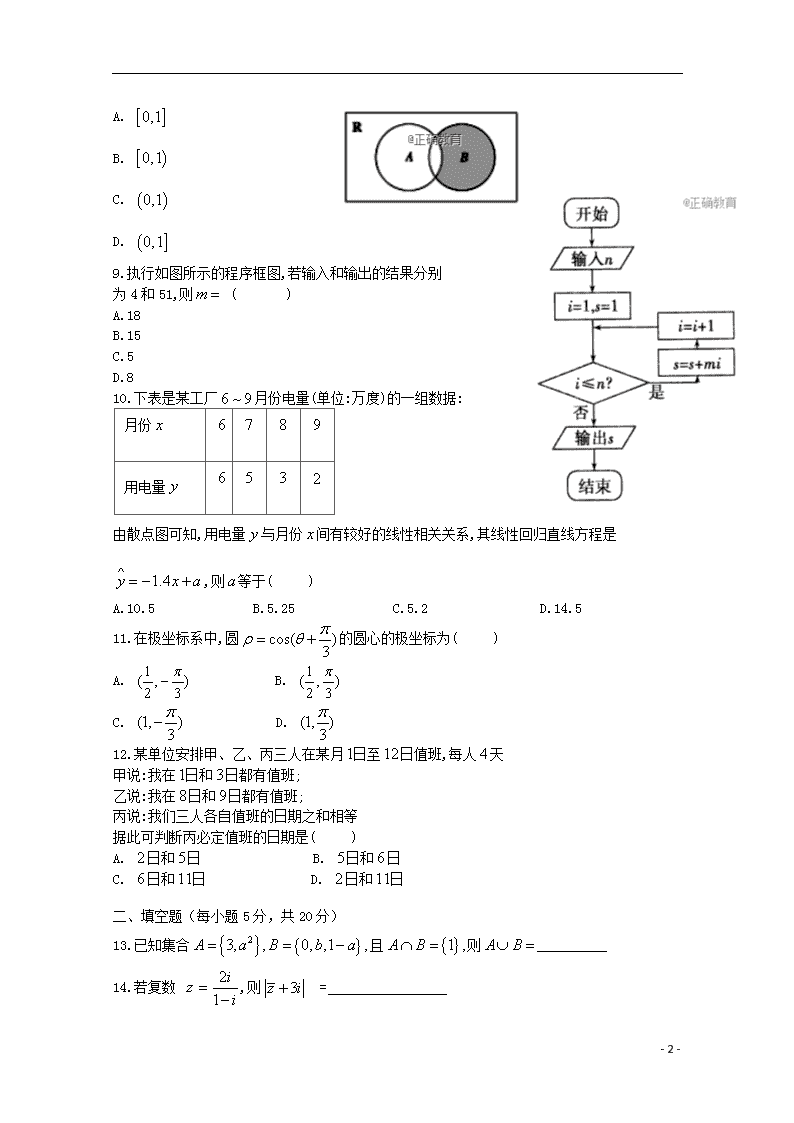
9.执行如图所示的程序框图,若输入和输出的结果分别
为4和51,则 ( )
A.18
B.15
C.5
D.8
10.下表是某工厂月份电量(单位:万度)的一组数据:
月份
用电量
由散点图可知,用电量与月份间有较好的线性相关关系,其线性回归直线方程是,则等于( )
A.10.5 B.5.25 C.5.2 D.14.5
11.在极坐标系中,圆的圆心的极坐标为( )
A. B.
C. D.
12.某单位安排甲、乙、丙三人在某月日至日值班,每人天
甲说:我在日和日都有值班;
乙说:我在日和日都有值班;
丙说:我们三人各自值班的日期之和相等
据此可判断丙必定值班的日期是( )
A. 日和日 B. 日和日
C. 日和日 D. 日和日
二、 填空题(每小题5分,共20分)
13.已知集合且则__________
14.若复数 ,则 =
- 9 -
15.极坐标系中两点和,则的中点的极坐标为__________
16.“三角形的外角至少有两个钝角”的否定是__________.
三、解答题(第17题10分,其余各题均12分.共70分)
17、(本小题满分10分)
已知函数,当时,求不等式的解集
18、 (本小题满分12分)
为了解某班学生喜好体育运动是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
喜好体育运动
不喜好体育运动
合计
男生
5
女生
10
合计
50
已知按喜好体育运动与否,采用分层抽样法抽取容量为10的样本,则抽到喜好体育运动的人数为6.
1.请将上面的列联表补充完整;
2.能否在犯错概率不超过的前提下认为喜好体育运动与性别有关?说明你的理由.
(参考公式: )
临界值表
0.15
0.10
0.05
0.025
0.010
0.005
0.001
2.072
2.706
3.841
5.024
6.635
7.879
10.828
19、(本小题满分12分)
已知函数
1.求曲线在点处的切线方程;
2.求函数的单调区间。
- 9 -
20、(本小题满分12分)
已知直线经过点,倾斜角.
1.写出直线的参数方程。
2.设与圆相交与两点,求点到两点的距离之和与距离之积。
21、(本小题满分12分)
在极坐标系中,曲线参数方程为,以极点为原点,极轴为轴的正半轴建立平面直角坐标系,直线的参数方程为参数
1.写出曲线的参数方程和直线的普通方程;
2.已知点是曲线上一点,求点到直线的最小距离.
22、(本小题满分12分)
已知函数
1.若 在上的最小值为,求的值;
2.若 在上恒成立,求的取值范围.
- 9 -
参考答案
一、选择题
1.答案:B
2.答案:D
3.答案:B
4.答案: A
5.答案: B
6.答案: A
7.答案:D
8.答案:D
9.答案:C
10.答案:D
11.答案:A
12.答案:C
解析:日期之和为,三人各自值班的日期之和相等,
故每人值班四天的日期之和是,
甲在日和日都有值班,
故甲余下的两天只能是号和号;
而乙在日和日都有值班, ,
所以号只能是丙去值班了.
余下还有号、号、号、号、号五天,
显然, 号只可能是丙去值班了
二、填空题
13.答案:
解析:
14.答案: 根号5
解析:
15.答案:
解析:
16.答案:存在一个三角形,其外角最多有一个钝角
解析:全称命题的否定形式为特称命题, 而"至少有两个"的否定为"至多有一个"故该命题的否定为"存在一个三角形,其外角最多有一个钝角"
三、解答题
17.答案:1.
时,即求解|
①当时,不等式即 ,解得
②当时,不等式即∴
- 9 -
③当时, ,解得,即
∴综上,解集为 或
2.
即恒成立
令,
则由函数的图象可得它的最大值为
故函数的图象应该恒在函数
的图象的上方,数形结合可得
∴,即的范围是
解析:
18.答案:1.设喜好体育运动的人数为人,由已知得解得列联表补充如下:
喜好体育运动
不喜好体育运动
合计
男生
女生
合计
2.∵
所以,可以在犯错概率不超过的前提下认为喜好体育运动与性别有关.
解析:
19.答案:1.解:因为
所以
所以又因为
所以曲线在点处的切线方程为即
2.因为函数的定义域为
- 9 -
由得;
得
所以函数的单调递减区间是单调递增区间为
解析:
20.答案:1.直线的参数方程为为参数
2.将直线的参数方程为参数
代入中得:
是方程的两个根,
解析:
21.答案:1.由曲线的极坐标方程得: ,
∴曲线的直角坐标方程为: ,
曲线的参数方程为为参数;
- 9 -
直线的普通方程为: .
2.设曲线上任意一点为,
则点到直线的距离为
解析:
22.答案:1. 由题意的定义域为且
∵,
故在上是单调递增函数.
2.由(1)可知,
①若,则,即在上恒成立,此时在上为增函数,
∴,∴ (舍去).
②若,则,即在上恒成立,此时在上为减函数,
∴,∴ (舍去).
③若,令得,
当时, ,∴在上为减函数;
当时, ,∴在上为增函数,
∴,∴
综上所述, .
3. ∵
又
令,
- 9 -
∵时, ,
∴在上是减函数.
∴,即,
∴在上也是减函数. ,
∴当时, 在上恒成立.
解析:
- 9 -