- 997.50 KB
- 2021-04-13 发布
总复习:空间向量在立体几何中的应用
【考纲要求】
1. 理解直线的方向向量与平面的法向量.
2. 能用向量语言表述直线与直线、直线与平面、平面与平面的垂直、平行关系.
3. 能用向量方法证明有关直线和平面位置关系的一些定理(包括三垂线定理).
4. 能用向量方法解决直线与直线、直线与平面、平面与平面的夹角的计算问题,了解向量方法在研究几何问题中的作用.
【知识网络】
【考点梳理】
空间向量在立体几何中的应用401056 知识要点】
考点一:立体几何中垂直和平行命题
对于垂直问题,一般是利用进行证明;
对于平行问题,一般是利用共线向量和共面向量定理进行证明.
考点二:立体几何中有关角的求解
利用向量求夹角(线线夹角、线面夹角、面面夹角)有时也很方便.其一般方法是将所求的角转化为求两个向量的夹角或其补角,而求两个向量的夹角则可以利用向量的夹角公式。
考点三:立体几何中有关距离的计算
设n是平面的法向量,AB是平面的一条斜线,则点B到平面的距离为(如图)。
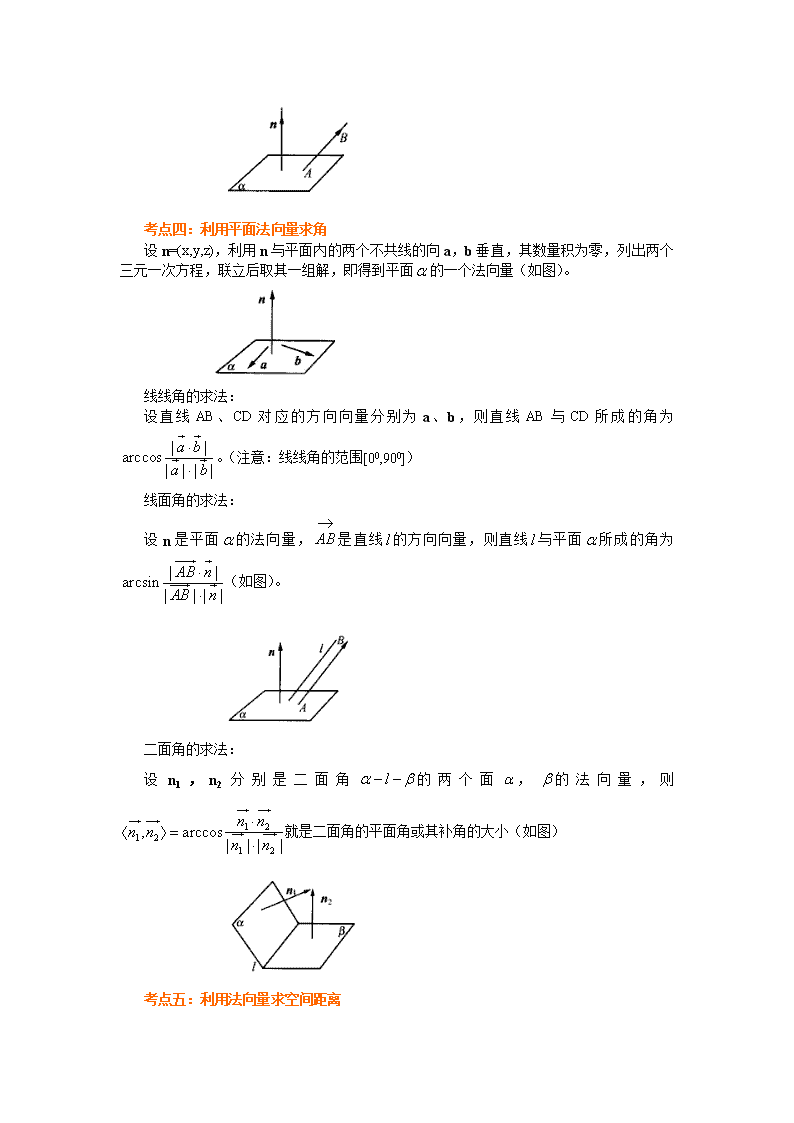
考点四:利用平面法向量求角
设n=(x,y,z),利用n与平面内的两个不共线的向a,b垂直,其数量积为零,列出两个三元一次方程,联立后取其一组解,即得到平面的一个法向量(如图)。
线线角的求法:
设直线AB、CD对应的方向向量分别为a、b,则直线AB与CD所成的角为。(注意:线线角的范围[00,900])
线面角的求法:
设n是平面的法向量,是直线的方向向量,则直线与平面所成的角为(如图)。
二面角的求法:
设n1,n2分别是二面角的两个面,的法向量,则就是二面角的平面角或其补角的大小(如图)
考点五:利用法向量求空间距离
⑴ 点A到平面的距离:
,其中,是平面的法向量。
⑵ 直线与平面之间的距离:
,其中,是平面的法向量。
⑶ 两平行平面之间的距离:
,其中, 是平面的法向量。
【典型例题】
类型一:利用空间向量证明有关平行或垂直
例1. 在正方体ABCD-A1B1C1D1中,E、F分别是BB1,CD的中点
(1)求证:AD⊥D1F;
(2)求AE与D1F所成的角;
(3)证明平面AED⊥平面A1FD1
【思路点拨】涉及正方体中一些特殊的点、线、面的问题,建立空间直角坐标系来解,不仅容易找到解题方向,而且坐标也简单,此时“垂直”问题转化为“两向量数量积为0”的问题,当然也可用其它的证法
【解析】建立空间直角坐标系如图,并设AB=2,
则A(0,0,0), D(0,2,0), A1(0,0,2) ,D1(0,2,2),E(2,0,1), F(1,2,0)
(1)证明:
∴=0×1+2×1+0×(-2)=0, ∴AD⊥D1F
(2)解:=(2,0,1), =(1,0,-2),| ,|
设AE与D1F的夹角为θ,
则cosθ=
所以,直线AE与D1F所成的角为90°.
(3)证明:由(1)知D1F⊥AD,由(2)知D1F⊥AE,
又AD∩AE=A,∴D1F⊥平面AED,
∵D1F平面A1FD1M
∴平面AED⊥平面A1FD1 。
【总结升华】用向量法证明垂直,就是证有关向量的数量积为0。
举一反三:
【变式1】如图,在棱长为2的正方体中,分别为、的中点,分别为与的中点.指出直线与平面的位置关系.
【解析】以AB、AA1、AD所在直线为x,y,z轴建立直角坐标系如图所示,
则B(2,0,0),C(2,2,0),D(0,2,0), A1(0,0,2),B1(2,0,2),C1(2,2,2),D1(0,2,2),
从而E(1,0,2),F(0,1,2),G(2,1,0),H(1,1,2),
,
∴,即,
又,∴.
类型二:利用空间向量求异面直线所成的角
例2.在正四面体ABCD中,E、F分别为AD、BC的中点,求异面直线AF、CE所成角的余弦值.
【思路点拨】求异面直线所成的角,可通过过某一点作异面直线的平行线,转化为求相交直线所成的角.这里因为E为AD的中点,故可取FD的中点G,由三角形的中位线定理知EG//AF,从而求AF、CE所成的角.
【解析】如图,连DF,取DF的中点G,连GE、GC,
∵E为AD的中点,∴EG//AF,
∴∠GEC即为AF、CE所成的角.
设正四面体的棱长为a, 则CE=AF=DF=a,
∴ EG=FG=a,在RtΔGFC中,CG==a.
∴在ΔECG中,由余弦定理可得:cos∠GEC==,
∴异面直线AF、CE所成的角的余弦值.
【总结升华】作异面直线所成的角常用的方法
①平移法:在异面直线中的一条直线上选择“特殊点”,作另一条直线的平行线或利用中位线;
②补形法:把空间图形补成熟悉的几何体,其目的在于容易发现两条异面直线间的关系.
一般来说,平移法是最常用的,应作为求两异面直线所成角的首选方法;
③向量法:用夹角公式.
举一反三:
【变式1】如图,正四棱柱中,,则异面直线所成角的余弦值为( )
A. B. C. D.
【解析】D;
设,则 ,以为坐标原点建立直角坐标系如图所示,
则,
所以异面直线所成角的余弦值为。
类型三:直线与平面所成的角
例3、正方体ABCD-EFGH的棱长为a,点P在AC上,Q在BG上,且AP=BQ=a, 求直线PQ与平面ABCD所成的角的正切值;
【思路点拨】先作出PQ在面ABCD内的射影,由于面BFGC⊥面ABCD,作QM⊥BC于M,则MP就是QP在面ABCD内的射影,∠QPM就是要求的角.
【解析】作QM⊥BC于M,连MP,
则∠QPM就是直线PQ与平面ABCD所成的角
易得:QM=, MP=(1-
∴tan∠QPM=
【总结升华】求直线和平面所成的角,关键是作出斜线在平面内的射影,将直线与平面所成的角转化成线线所成的角.
举一反三:
【变式1】如图,三棱锥P-ABC中,∠ABC=,PA=1,AB=,AC=2,PA⊥面ABC.
(1)求直线AB和直线PC所成角的余弦值;
(2)求PC和面ABC所成角的正弦值;
【解析】(1)以A为坐标原点,分别以AB、AP所在直线为y轴、z轴,以过A点且平行于BC直线为x轴建立空间直角坐标系.
在直角△ABC中,∵AB=,AC=2,∴BC=1
A(0,0,0),B(0,,0),C(1,,0),P(0,0,1).
(0,,0),(1,,),
cos<,>===
∴直线AB与直线PC所成的角余弦为.
(2)取平面ABC的一个法向量=(0,0,1),
设PC和面ABC所成的角为,则
sin=|cos<,>|==.
∴PC和面ABC所成的角的正弦值为.
类型四:有关二面角问题
例4(2018 惠州模拟)如图,在四棱锥P﹣ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=AD=1,CD=.
(1)求证:平面PQB⊥平面PAD;
(2)若二面角M﹣BQ﹣C为30°,设PM=tMC,试确定t的值.
【解析】(Ⅰ)证法一:∵AD∥BC,BC=AD,Q为AD的中点,
∴四边形BCDQ为平行四边形,∴CD∥BQ.
∵∠ADC=90°∴∠AQB=90°,即QB⊥AD.
又∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,
∴BQ⊥平面PAD.
∵BQ⊂平面PQB,∴平面PQB⊥平面PAD.
证法二:AD∥BC,BC=AD,Q为AD的中点,
∴四边形BCDQ为平行四边形,∴CD∥BQ.
∵∠ADC=90°∴∠AQB=90°.
∵PA=PD,∴PQ⊥AD.
∵PQ∩BQ=Q,∴AD⊥平面PBQ.
∵AD⊂平面PAD,∴平面PQB⊥平面PAD
(Ⅱ)∵PA=PD,Q为AD的中点,∴PQ⊥AD.
∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,
∴PQ⊥平面ABCD.
如图,以Q为原点建立空间直角坐标系.
则平面BQC的法向量为;
Q(0,0,0),,,.
设M(x,y,z),则,,
∵,
∴,∴
在平面MBQ中,,,
∴平面MBQ法向量为.
∵二面角M﹣BQ﹣C为30°,
∴,
∴t=3.
举一反三:
【变式1】(2018 漳州二模)如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
(Ⅰ)求证:AC⊥平面BDE;
(Ⅱ)求二面角F﹣BE﹣D的余弦值;
(Ⅲ)设点M是线段BD上一个动点,试确定点M的位置,使得AM∥平面BEF,并证明你的结论.
【证明】(Ⅰ)因为DE⊥平面ABCD,所以DE⊥AC.
因为ABCD是正方形,所以AC⊥BD,
从而AC⊥平面BDE.
【解析】(Ⅱ)因为DA,DC,DE两两垂直,所以建立空间直角坐标系D﹣xyz如图所示.
因为BE与平面ABCD所成角为600,即∠DBE=60°,
所以.
由AD=3,可知,.
则A(3,0,0),,,B(3,3,0),C(0,3,0),
所以,.
设平面BEF的法向量为=(x,y,z),则,即.
令,则=.
因为AC⊥平面BDE,所以为平面BDE的法向量,.
所以,
因为二面角为锐角,所以二面角F﹣BE﹣D的余弦值为
(Ⅲ)点M是线段BD上一个动点,设M(t,t,0).
则.
因为AM∥平面BEF,
所以=0,即4(t﹣3)+2t=0,解得t=2.
此时,点M坐标为(2,2,0),
即当时,AM∥平面BEF
类型五:利用空间向量求空间距离
例5.如图,四面体ABCD中,O、E分别是BD、BC的中点,,,求点E到平面ACD的距离。
【解析】以O为原点,如图建立空间直角坐标系,
则
设平面ACD的法向量为则
,令得是平面ACD的一个法向量。
又
点E到平面ACD的距离
【总结升华】求点到平面的距离除了根据定义及等积变换外,还可以借用平面的法向量求得,方法是:求出平面的一个法向量的坐标(两种方法),再求出已知点P与平面内任一点M构成的向量的坐标,那么P到平面的距离d=|||cos〈,〉。
举一反三:
【变式1】在平行四边形ABCD中,AB=AC=1,∠ACD=90°,将它沿对角线AC折起,使AB与CD成60°角,求B、D间的距离
【解析】如下图,
因为∠ACD=90°,所以· =0,
同理,·=0
因为AB与CD成60°角,所以〈,〉=60°或120°
因为=++,
所以
所以||=2或,
即B、D间的距离为2或。
类型六:空间向量在立体几何中的综合应用
例6. 如图,在三棱锥中,,,,.
A
C
B
P
(Ⅰ)求证:;
(Ⅱ)求二面角的正弦值;
(Ⅲ)求点到平面的距离.
解析:
(Ⅰ)取中点,连结.
A
C
B
D
P
,.
,.
,
平面.
平面,
.
A
C
B
E
P
(Ⅱ),,.
又,.
又,即,且,
平面.
取中点.连结.
,.
是在平面内的射影,.
是二面角的平面角.
在中,,,,
.
A
C
B
D
P
H
二面角的正弦值为.
(Ⅲ)由(Ⅰ)知平面,
平面平面.
过作,垂足为.
平面平面,
平面.
的长即为点到平面的距离.
由(Ⅰ)知,又,且,
平面.
平面,
.
在中,,,
.
.
点到平面的距离为.
举一反三:
【变式1】如图,在直四棱柱中,已知,,.
B
C
D
A
E
G
(Ⅰ)设是的中点,求证:平面;
(Ⅱ)求二面角的余弦值.
【解析】(Ⅰ)连结,则四边形为正方形,
,且,
四边形为平行四边形..
又平面,平面,
平面.
(Ⅱ)以为原点,所在直线分别为轴,轴,轴建立如图所示的空间直角坐标系,
B
C
D
A
E
z
y
x
F
M
不妨设,则,,,,,
,,
设为平面的一个法向量.
由,,得 取,则.
又,,
设为平面的一个法向量,
由,,得取,则,
设与的夹角为,二面角为,显然为锐角,
.,
即所求二面角的余弦为.