- 432.50 KB
- 2021-04-13 发布
哈师大附中高二上学期期末考试
理科数学试题
一.选择题(本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.抛物线的焦点坐标为( )
A.() B.() C.() D.()
2.将两颗骰子各掷一次,设事件A=“两个点数都是偶数”,则概率等于( )
A. B. C. D.
3.已知点为椭圆的两个焦点,过的直线交椭圆于两点,且,则( )
A.20 B.18 C.12 D.10
4.在极坐标系中,圆的圆心的极坐标为( )
A. B. C. D.
5.某单位共有老、中、青职工430人,其中有青年职工160人,中年职工人数是老年职工人数的2倍.为
了解职工身体状况,现采用分层抽样方法进行调查,在抽取的样本中有青年职工32人,则该样本中的
老年职工抽取人数为( )
A.9 B.18 C.27 D.36
6.设集合,则“”是“”的( )
A.充分而不必要条件 B.必要而不充分条件 C. 充分必要条件 D.既不充分也不必要条件
7.已知P是抛物线上的一个动点,则点P到直线和的距离之和的最小值是( )
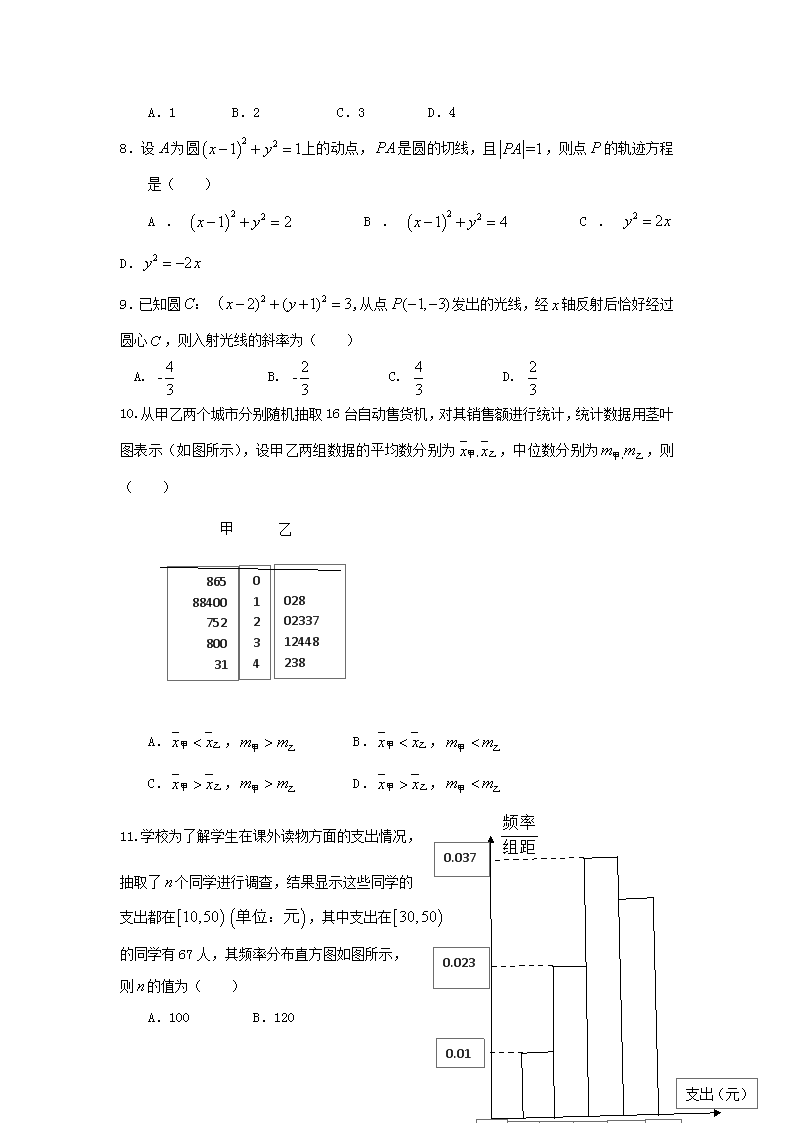
A.1 B.2 C.3 D.4
8.设为圆上的动点,是圆的切线,且,则点的轨迹方程是( )
A. B. C. D.
9.已知圆,从点发出的光线,经轴反射后恰好经过圆心,则入射光线的斜率为( )
A. B. C. D.
10.从甲乙两个城市分别随机抽取16台自动售货机,对其销售额进行统计,统计数据用茎叶图表示(如图所示),设甲乙两组数据的平均数分别为,中位数分别为,则( )
甲
乙
0
1
2
3
4
028
02337
12448
238
865
88400
752
800
31
A., B.,
C., D.,
支出(元)
0
10
20
30
40
50
0.01
0.023
0.037.
11.学校为了解学生在课外读物方面的支出情况,
抽取了个同学进行调查,结果显示这些同学的
支出都在,其中支出在
的同学有67人,其频率分布直方图如图所示,
则的值为( )
A.100 B.120
C.130 D.390
12.从6名同学中选派4人分别参加数学、物理、化学、生物四科知识竞赛,若其中甲、乙两名同学不能参加生物竞赛,则选派方案共有( )种
A.336 B.408 C.240 D.264
二.填空题(本大题共4小题,每小题5分)
13.在三棱锥中,三条侧棱两两垂直,且侧棱长都是1,则点到平面的距离为 .
14.从区间内任取两个数,则这两个数的和小于的概率为________________.
15.的展开式中各项系数的和为-32,则该展开式中系数最大的项为________________.
16.设是双曲线在第一象限内的点,为其右焦点,点关于原点的对称点为若设且则双曲线离心率的取值范围是 .
三.解答题(本大题共6小题,总分70分)
17.(本题满分10分)在新年联欢晚会上,游戏获胜者甲和乙各有一次抽奖机会,共有10个奖品,其中一等奖6个,二等奖4个,甲、乙二人依次各抽一次.
(1)甲抽到一等奖且乙抽到二等奖的概率是多少?
(2)甲、乙二人中至少有一人抽到一等奖的概率是多少?
18.(本题满分12分)在平面直角坐标系中,直线的参数方程为: (
为参数),它与曲线交于,两点.
(1) 求的长;
(2)在以为极点,轴的正半轴为极轴建立极坐标系,设点的极坐标为,求点到线段中点的距离.
19. (本题满分12分)已知四棱锥中,底面是矩形,平面,,是的中点,是线段上的点.
(1)当是的中点时,求证:平面.
(2)当时,求二面角的余弦值.
F
E
P
D
C
A
B
20.(本题满分12分)抛物线:的焦点为,抛物线上点M的横坐标为2,且
(1)求抛物线的方程;
(2)过焦点作两条相互垂直的直线,分别与抛物线交于、和、四点,求四边形 面积的最小值.
21.(本题满分12分)已知在长方体中,,,点E在棱
A
B
C
D
E
上移动.
(1)求证:;
(2)在棱AB上是否存在点E使得与平面成的角为?若存在,求出AE的长,若不存在,说明理由.
22.(本题满分12分)椭圆的左右焦点分别为,离心率为,过点且垂直于x轴的直线被椭圆截得的弦长为,直线与椭圆交于不同的,两点.
(1)求椭圆的方程;
(2)若在椭圆上存在点满足:(为坐标原点).求实数的取值范围.
1
2
3
4
5
6
7
8
9
10
11
12
D
A
C
A
B
A
C
A
C
B
A
C
一、选择题
二、填空题
13、 14、 15、 16、
三、解答题
17、(1) (2)
18、(1) (2)
19、(1)略 (2)
20、(1) (2)32
21、(1)略 (2)
22、(1) (2)