2018届二轮复习平抛运动课件（60张）全国通用 60页

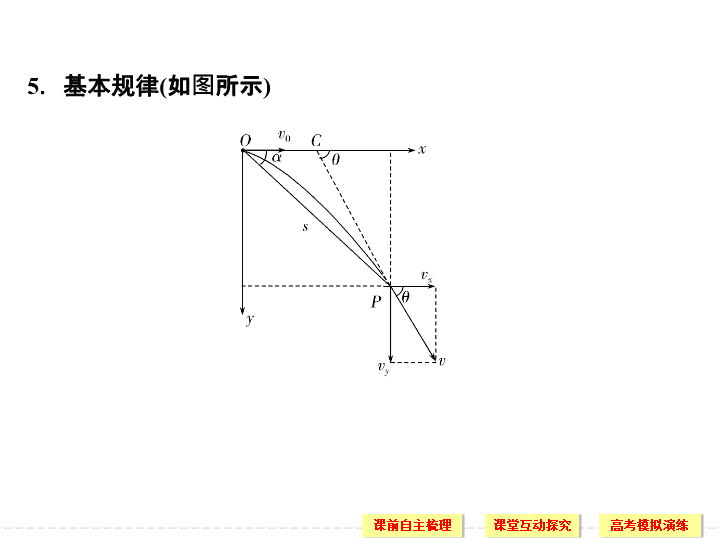
基础课 2 　平抛运动 知识点一、平抛运动 1 ． 定义： 把物体 以一定的初速度沿水平方向抛出 ，不考虑空气阻力，物体 只在 _____ 作用下 所做的 运动。 2 ． 性质 ：平抛运动是加速度为 g 的 ________ 曲线运动，其运动轨迹是 _________ 。 3 ． 平抛运动的条件： (1) v 0 ≠ 0 ，沿 ___________ ； (2) 只受 _____ 作用。 4 ． 研究方法： 平抛运动可以分解为水平方向的 _________ 运动和竖直方向的 _________ 运动。 重力 匀加速 抛物线 水平方向 重力 匀速直线 自由落体 5 ． 基本规律 ( 如图所示 ) (1) 速度关系 (2) 位移关系 (3) 轨迹方程： y ＝ ____________ gt v 0 t 知识点二、斜抛运动 1 ． 定义： 以初速度将物体与水平方向成一定角度 ________ 抛出，物体仅在 ______ 作用下所做的曲线运动。 2 ． 性质 ：加速度为 _______________ 的匀变速曲线运动，轨迹是 _________ 。 3 ． 研究方法： 斜抛运动可以看做水平方向的 ___________ 运动和竖直方向的 ____________ 运动的合运动。 重力加速度 g 抛物线 匀速直线 匀变速直线 斜向上 重力 [ 思考判断 ] (1) 平抛运动是匀变速曲线运动。 ( 　　 ) (2) 平抛运动的加速度方向时刻在变化。 ( 　　 ) (3) 平抛运动的竖直分运动是自由落体运动。 ( 　　 ) (4) 平抛运动的物体任意时刻速度方向与水平方向的夹角保持不变。 ( 　　 ) (5) 平抛运动的物体在任意相等的两段时间内的速度的变化相同。 ( 　　 ) (6) 对于在相同高度以相同速度平抛的物体，在月球上水平位移与在地球上水平位移相等。 ( 　　 ) 答案　 (1) √ 　 (2) × 　 (3) √ 　 (4) × 　 (5) √ 　 (6) × 平抛运动的规律及其应用 4 ． 速度改变量： 物体在任意相等时间内的速度改变量 Δ v ＝ g Δ t 相同，方向恒为竖直向下，如图 1 所示。 图 1 图 2 (2) 做平抛 ( 或类平抛 ) 运动的物体在任一时刻，设其速度方向与水平方向的夹角为 θ ，位移与水平方向的夹角为 α ，则 tan θ ＝ 2tan α 。如图 2 所示。 推导： 1 ． [ 对平抛运动的理解 ] ( 多选 ) 对于平抛运动，下列说法正确的是 ( 　　 ) A ．落地时间和落地时的速度只与抛出点的高度有关 B ．平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动 C ．做平抛运动的物体，在任何相等的时间内位移的增量都是相等的 D ．平抛运动是加速度大小、方向不变的曲线运动 答案　 BD 2 ． [ 平抛规律的应用 ] ( 多选 ) 某人向放在水平地面上正前方的小桶中水平抛球，结果球划着一条弧线飞到小桶的前方，如图 3 所示。不计空气阻力，为了能把小球抛进小桶中，则下次再水平抛球时，可能做出的调整为 ( 　　 ) 图 3 A ．减小初速度，抛出点高度不变 B ．增大初速度，抛出点高度不变 C ．初速度大小不变，降低抛出点高度 D ．初速度大小不变，增大抛出点高度 答案　 AC 3 ． [ 多体的平抛运动 ] 如图 4 所示，在同一平台上的 O 点水平抛出的三个物体分别落到 a 、 b 、 c 三点，不计空气阻力，则三个物体运动的初速度 v a 、 v b 、 v c 的关系和三个物体运动的时间 t a 、 t b 、 t c 的关系分别是 ( 　　 ) 图 4 A ． v a ＞ v b ＞ v c ； t a ＞ t b ＞ t c B ． v a ＜ v b ＜ v c ； t a ＝ t b ＝ t c C ． v a ＜ v b ＜ v c ； t a ＞ t b ＞ t c D ． v a ＞ v b ＞ v c ； t a ＜ t b ＜ t c 答案　 C “ 化曲为直 ” 思想在平抛运动中的应用 (1) 根据运动效果的等效性，利用运动分解的方法，将其转化为我们所熟悉的两个方向上的直线运动： ① 水平方向的匀速直线运动； ② 竖直方向的自由落体运动。 (2) 运用运动合成的方法求出平抛运动的速度、位移等。 反思总结 与斜面相关联的平抛运动 【典例】 　 (2017· 信阳一模改编 ) 如图 5 所示，一名跳台滑雪运动员经过一段时间的加速滑行后从 O 点水平飞出，经过 3 s 落到斜坡上的 A 点。已知 O 点是斜坡的起点，斜坡与水平面的夹角 θ ＝ 37° ，不计空气阻力 (sin 37° ＝ 0.6 ， cos 37° ＝ 0.8 ， g 取 10 m/s 2 ) 。则运动员落到斜坡上时速度方向与水平方向的夹角 φ 满足 ( 　　 ) 图 5 A ． tan φ ＝ 1.33 B ． tan φ ＝ 1.44 C ． tan φ ＝ 1.50 D ． tan φ ＝ 2.00 答案　 C 【 思考 延伸】 在 【典例】 中，若运动员从 O 点飞出的初速度为 20 m/s ，则运动员离开 O 点后离斜坡的最远距离为 ( 　　 ) A ． 30 m B ． 15 m C ． 18 m D ． 9m 解析　 将运动员的初速度 v 0 和加速度 g 分别沿垂直于斜面和平行于斜面方向进行分解，如图所示，初速度 v 0 沿垂 直斜面方向上的分量为 v 1 ＝ v 0 sin θ ，加速度 g 在垂直于斜面方向上的分量为 a 1 ＝ g cos θ ，根据分运动各自独立的原理可知， 答案　 D 平抛运动的分解方法与技巧 (1) 如果知道速度的大小或方向，应首先考虑分解速度。 (2) 如果知道位移的大小或方向，应首先考虑分解位移。 (3) 两种分解方法： ① 沿水平方向的匀速运动和竖直方向的自由落体运动； ② 沿斜面方向的匀加速运动和垂直斜面方向的匀减速运动。 技巧点拨 1 ．将一挡板倾斜 地固定在水平面上，倾角为 θ ＝ 30° ，如图 6 所示。现有质量为 m 的小球由挡板上方的 A 点以 v 0 的初速度水平向右抛出，小球落在挡板上的 B 点时，小球速度方向刚好与挡板垂直，小球与挡板碰前后的速度方向相反、速度大小之比为 4 ∶ 3 。下列有关小球的运动描述正确的是 ( 　　 ) 图 6 解析　 小球在碰撞挡板前做平抛运动。设刚要碰撞斜面时小球速度为 v 。由题意，速度 v 的方向与竖直方向的夹角为 30° 且水平分量仍为 v 0 ，如图。由此得 v ＝ 2 v 0 ，碰撞过程中， 答案　 D 2 ． [ 分解速度和位移的综合应用 ] ( 多选 ) 如图 7 所示，一固定斜面倾角为 θ ，将小球 A 从斜面顶端以速率 v 0 水平向右抛出，击中了斜面上的 P 点；将小球 B 从空中某点以相同速率 v 0 水平向左抛出，恰好垂直斜面击中 Q 点。不计空气阻力，重力加速度为 g ，下列说法正确的是 ( 　　 ) 图 7 A ．若小球 A 在击中 P 点时速度方向与水平方向所夹锐角为 φ ，则 tan θ ＝ 2tan φ B ．若小球 A 在击中 P 点时速度方向与水平方向所夹锐角为 φ ，则 tan φ ＝ 2tan θ C ．小球 A 、 B 在空中运动的时间比为 2tan 2 θ ∶ 1 D ．小球 A 、 B 在空中运动的时间比为 tan 2 θ ∶ 1 答案　 BC 平抛运动中的临界问题 常见的 “ 三种 ” 临界特征 (1) 有些题目中有 “ 刚好 ” 、 “ 恰好 ” 、 “ 正好 ” 等字眼，明显表明题述的过程中存在着临界点。 (2) 若题目中有 “ 取值范围 ” 、 “ 多长时间 ” 、 “ 多大距离 ” 等词语，表明题述的过程中存在着 “ 起止点 ” ，而这些起止点往往就是临界点。 (3) 若题目中有 “ 最大 ”“ 最小 ”“ 至多 ”“ 至少 ” 等字眼，表明题述的过程中存在着极值，这个极值点往往是临界点。 【典例】 　 (2016· 浙江理综， 23) 在真空环境内探测微粒在重力场中能量的简化装置如图 8 所示。 P 是一个微粒源，能持续水平向右发射质量相同、初速度不同的微粒。高度为 h 的探测屏 AB 竖直放置，离 P 点的水平距离为 L ，上端 A 与 P 点的高度差也为 h 。 图 8 (1) 若微粒打在探测屏 AB 的中点，求微粒在空中飞行的时间； (2) 求能被屏探测到的微粒的初速度范围； (3) 若打在探测屏 A 、 B 两点的微粒的动能相等，求 L 与 h 的关系。 1 ． 处理平抛运动中的临界问题要抓住两点 (1) 找出临界状态对应的临界条件； (2) 要用分解速度或者分解位移的思想分析平抛运动的临界问题。 2 ． 平抛运动临界极值问题的分析方法 (1) 确定研究对象的运动性质； (2) 根据题意确定临界状态； (3) 确定临界轨迹，画出轨迹示意图； (4) 应用平抛运动的规律结合临界条件列方程求解。 方法技巧 1 ． [ 生活中的临界问题 ] [2016· 广东广州综合测试 ( 一 )] 如图 9 ，窗子上、下沿间的高度 H ＝ 1.6 m ，墙的厚度 d ＝ 0.4 m ，某人在离墙壁距离 L ＝ 1.4 m 、距窗子上沿 h ＝ 0.2 m 处的 P 点，将可视为质点的小物件以 v 的速度水平抛出，小物件直接穿过窗口并落在水平地面上，取 g ＝ 10 m/s 2 。则 v 的取值范围是 ( 　　 ) A ． v ＞ 7 m/s B ． v ＜ 2.3 m/s C ． 3 m/s ＜ v ＜ 7 m/s D ． 2.3 m/s ＜ v ＜ 3 m/s 图 9 答案　 C 2 ． [ 平抛运动与斜面有关的临界问题 ] 如图 10 为湖边一倾角为 30° 的大坝横截面示意图，水面与大坝的交点为 O 。一人站在 A 点以速度 v 0 沿水平方向扔一小石子，已知 AO ＝ 40 m ，不计空气阻力， g 取 10 m/s 2 。下列说法中正确的是 ( 　　 ) 图 10 A ．若 v 0 ＞ 18 m/s ，则石子可以落入水中 B ．若 v 0 ＜ 20 m/s ，则石子不能落入水中 C ．若石子能落入水中，则 v 0 越大，落水时速度方向与水平面的夹角越大 D ．若石子不能落入水中，则 v 0 越大，落到斜面上时速度方向与斜面的夹角越大 答案　 A 生活中的平抛运动问题 平抛运动与日常生活紧密联系，如乒乓球、足球、排球等运动模型，飞镖、射击、飞机投弹模型等。这些模型经常受到边界条件的制约，如网球是否触网或越界、飞镖是否能击中靶心、飞机投弹是否能命中目标等。解题的关键是能准确地运用平抛运动规律分析对应的运动特征。 图 11 A ．击球点的高度与网高度之比为 2 ∶ 1 B ．乒乓球在网左右两侧运动时间之比为 2 ∶ 1 C ．乒乓球过网时与落到右侧桌边缘时速率之比为 1 ∶ 2 D ．乒乓球在左、右两侧运动速度变化量之比为 1 ∶ 2 答案　 D 图 12 答案　 B 处理此类问题的方法 (1) 阅读试题，提炼关键信息； (2) 通过迁移、联想、类比，建立物理模型； (3) 找出每个物理过程所满足的规律，应用所 反思总结 学知识列方程，进行推理计算，得出结论。 体育运动中许多运动都可简化为平抛运动的模型，在分析此类问题时一定要注意从实际出发寻找一些临界点，画出物体运动的草图，找出临界条件，如图所示的网球刚好过网和刚好压线的情况。 1 ． (2016· 海南单科， 1) 在地面上方某一点将一小球以一定的初速度沿水平方向抛出，不计空气阻力，则小球在随后的运动中 ( 　　 ) A ．速度和加速度的方向都在不断变化 B ．速度与加速度方向之间的夹角一直减小 C ．在相等的时间间隔内，速率的改变量相等 D ．在相等的时间间隔内，动能的改变量相等 答案　 B 2 ． ( 全国卷 ) ( 多选 ) 如图 13 所示， x 轴在水平地面内， y 轴沿竖直方向。图中画出了从 y 轴上沿 x 轴正向抛出的三个小球 a 、 b 和 c 的运动轨迹，其中 b 和 c 是从同一点抛出的。不计空气阻力，则 ( 　　 ) 图 13 A ． a 的飞行时间比 b 的长 B ． b 和 c 的飞行时间相同 C ． a 的水平速度比 b 的小 D ． b 的初速度比 c 的大 答案　 BD 3 ． (2015· 全国卷 Ⅰ ， 18) 一带有乒乓球发射机的乒乓球台如图 14 所示。水平台面的长和宽分别为 L 1 和 L 2 ，中间球网高度为 h 。发射机安装于台面左侧边缘的中点，能以不同速率向右侧不同方向水平发射乒乓球，发射点距台面高度为 3 h 。不计空气的作用，重力加速度大小为 g 。若乒乓球的发射速率 v 在某范围内，通过选择合适的方向，就能使乒乓球落到球网右侧台面上，则 v 的最大取值范围是 ( 　　 ) 图 14 答案 　 D 图 15 答案　 D