2020届高三物理上学期第一次月考试题（含解析）人教版 11页

‎2019届高三（上）第一次月考物理试卷 一、选择题 ‎1. 如图所示，坐高铁从杭州到南京，原需经上海再到南京，其路程为s1，位移为x1．杭宁高铁通车后，从杭州可直达南京．其路程为s2，位移为x2，则（　　）‎ A. s1＞s2，x1＞x2 B. s1＞s2，x1＜x2 C. s1＞s2，x1=x2 D. s1=s2，x1=x2‎ ‎【答案】C 考点：路程和位移 ‎【名师点睛】本题考查位移与路程，要注意明确位移是矢量，能表示物体位置的变化；而路程描述物体经过的轨迹的长度.‎ ‎2. 一质点做直线运动，其运动的位移x跟时间t的比值与时间t的关系图线为一条过原点的倾斜直线，如图所示．由图可知，t=2s时质点的速度大小为（　　）‎ A. 2m/s B. 4m/s C. 6m/s D. 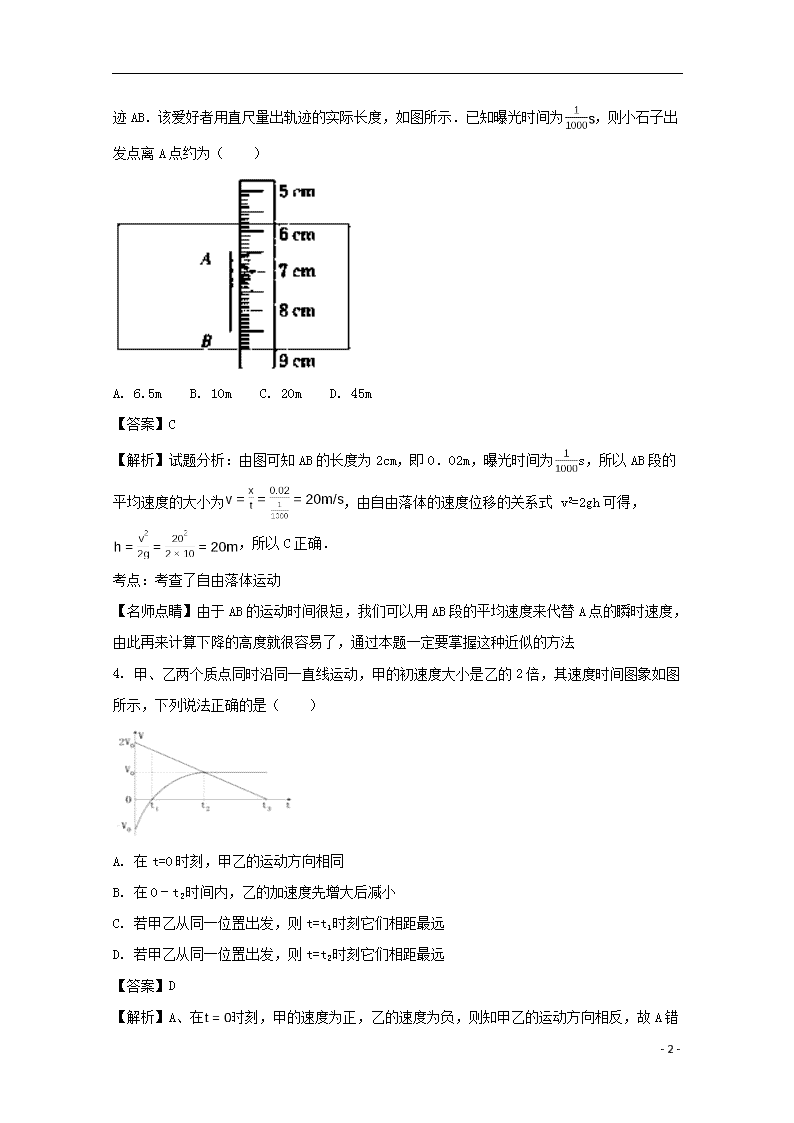8m/s ‎【答案】B ‎【解析】试题分析：由图得：．由匀变速直线运动的位移时间公式变形得：，可得质点的初速度v0=0，加速度为：a=2m/s2，质点做匀加速直线运动．所以t=2s时质点的速度大小为：v=at=4m/s 故选 考点：‎ ‎【名师点睛】‎ ‎3.‎ - 11 -‎ ‎ 一个小石子从离地某一高度处由静止自由落下，某摄影爱好者恰好拍到了它下落的一段轨迹AB．该爱好者用直尺量出轨迹的实际长度，如图所示．已知曝光时间为，则小石子出发点离A点约为（　　）‎ A. 6.5m B. 10m C. 20m D. 45m ‎【答案】C ‎【解析】试题分析：由图可知AB的长度为2cm，即0．02m，曝光时间为s，所以AB段的平均速度的大小为，由自由落体的速度位移的关系式 v2=2gh可得，，所以C正确．‎ 考点：考查了自由落体运动 ‎【名师点睛】由于AB的运动时间很短，我们可以用AB段的平均速度来代替A点的瞬时速度，由此再来计算下降的高度就很容易了，通过本题一定要掌握这种近似的方法 ‎4. 甲、乙两个质点同时沿同一直线运动，甲的初速度大小是乙的2倍，其速度时间图象如图所示，下列说法正确的是（　　）‎ A. 在t=0时刻，甲乙的运动方向相同 B. 在0﹣t2时间内，乙的加速度先增大后减小 C. 若甲乙从同一位置出发，则t=t1时刻它们相距最远 D. 若甲乙从同一位置出发，则t=t2时刻它们相距最远 ‎【答案】D ‎【解析】A、在 - 11 -‎ 时刻，甲的速度为正，乙的速度为负，则知甲乙的运动方向相反，故A错误； B、速度时间图线的斜率表示加速度，则知在时间内，乙的加速度一直减小，故B错误； C、甲一直沿正向运动，乙先沿负向运动，后沿正向运动，两者都沿正向运动时，若甲乙从同一位置出发，时刻前，甲的速度较大，两者间距增大，时刻后，乙的速度较大，两者间距减小，故时刻它们相距最远，故C错误，D正确。‎ 点睛：速度时间图线的斜率表示加速度，图线与时间轴围成的面积表示位移，分析速度的大小判断何时两个物体相距最远。‎ ‎5. 如图所示的位移﹣时间（x﹣t）图象和速度（V﹣t）图象中，给出了四条曲线1、2、3、4代表四个不同物体的运动情况，则下列说法错误的是（　　）‎ A. 图线1、3表示物体做曲线运动 B. X﹣t图象中0～t1时间内物体1和2的平均速度相等 C. V﹣t图象中t3时刻物体3的速度大于物体4的速度 D. 两图象中t2、t4时刻分别表示物体2和4开始反向运动 ‎【答案】ACD ‎【解析】A、运动图象反映物体的运动规律，不是运动轨迹，无论速度-时间图象还是位移-时间图象只能表示物体做直线运动，故A错误； B、图象中时间内物体1和2通过的位移相等，所用时间相等，则平均速度相等，故B正确； C、由图知，图象中时刻物体3的速度等于物体4的速度，故C错误； D、图线的斜率等于物体的速度，斜率大于0，表示物体沿正方向运动；斜率小于0，表示物体沿负方向运动，而时刻之前物体2的运动沿正方向，时刻之后物体2沿负方向运动，故时刻开始反向运动，图象中速度的正负表示运动方向，从这段时间内速度始终为正，故时刻没有反向运动，故D错误。‎ 点睛：对于图线和图线的基本的特点、意义一定要熟悉，这是我们解决这类问题的金钥匙，在学习中要多多积累。‎ - 11 -‎ ‎6. 汽车B在平直公路上行驶，发现前方沿同方向行驶的汽车A速度较小，为了避免相撞，距A车25m处B车制动，此后它们的v﹣t图象如图所示，则（　　）‎ A. B的加速度大小为3.75m/s2 B. A、B在t=4s时的速度相同 C. A、B在0～4s内的位移相同 D. A、B两车不会相撞 ‎【答案】BD ‎...............‎ 考点：v-t图线 ‎【名师点睛】在速度时间图象中，某一点代表此时刻的瞬时速度，时间轴上方速度是正数，时间轴下方速度是负数；切线表示加速度，加速度，向右上方倾斜，加速度为正，向右下方倾斜加速度为负；图象与坐标轴围成面积代表位移，时间轴上方位移为正，时间轴下方位移为负.‎ ‎7. 汽车自O点出发从静止开始在平直公路上做匀加速直线运动，途中在6s钟内分别经过P、Q两根电杆，已知P、Q电杆相距60m，车经过电杆Q时的速率是15m/s，则（　　）‎ A. 经过P杆时的速率是5m/s B. 车的加速度是1.5m/s2‎ C. P、O间距离是7.5m D. 车从出发到Q所用的时间是9s ‎【答案】ACD ‎【解析】试题分析：A、根据匀变速直线运动的平均速度公式 - 11 -‎ 所以有 则vP=5m/s 故A正确．‎ B、根据加速度的定义 ‎＞1.5m/s2‎ 故B错误．‎ C、根据速度位移关系有 ‎=‎ 故C正确．‎ D、根据速度公式有vQ=at 故D正确．‎ 故选：ACD．‎ ‎8. 为了保障2015年春运的行车安全，多地交警部门于2015年春季在新开通的高速公路上安装了固定雷达测速仪（如图所示），可以准确抓拍超速车辆以及测量运动车辆的运动情况，假设有一辆汽车（向着测速仪行驶）与固定雷达测速仪相距x（单位：m）时紧急刹车（刹车后可视为匀减速直线运动），汽车刹车的同时固定雷达测速仪发出超声波，当测速仪接收到反射回来的超声波信号时该汽车恰好停下，此时该汽车与固定雷达测速仪相距x0（单位：m），已知超声波速度为v0（单位：m/s），则根据以上信息能求得（　　）‎ A. 汽车刹车后的位移 B. 汽车刹车后的运动阻力 C. 汽车刹车后的运动时间 D. 汽车刹车后的加速度 ‎【答案】ACD - 11 -‎ ‎【解析】A、在整个这段时间内汽车的位移，即刹车后的位移，故A正确；‎ B、由于汽车的质量未知，根据牛顿第二定律无法求出汽车刹车后运动的阻力，故B错误；‎ C、汽车刹车后的时间，可以求出C正确；‎ D、超声波从发出到汽车和从汽车反射到测试仪的时间相等，采用逆向思维，汽车做初速度为零的匀加速直线运动，相等时间内的位移之比为，则相等的时间，因为相等时间内的位移大小可以求出，根据连续相等时间内的位移之差是一恒量可以求出汽车刹车后的加速度大小，故D正确。 点睛：解决本题的关键理清运动过程，抓住超声波从发出到汽车和从汽车反射到测试仪的时间相等，运用匀变速直线运动的规律进行求解。‎ 二、非选择题（一）必考题 ‎9. 如图所示为接在50Hz低压交流电源上的打点计时器在纸带做匀加速直线运动时打出的一条纸带，图中所标的是每5个计时点取一个计数点A、B、D、E等，但第三个计数点C未标出，由图中给出的数据计算纸带运动的加速度是a=__m/s2；在打下计数点B时，纸带运动的瞬时速度 vB=__m/s．（其中用s1表示A、B间距离，用s4表示D、E间距离，结果保留3位有效数字）‎ ‎【答案】 (1). 2.00 (2). 0.383‎ ‎【解析】试题分析: 根据匀变速直线运动的推论公式△x=aT2，有：DE-AB=3aT2，解得：a=2.00m/s2；‎ 由于△x=DE-CD=CD-BC=BC-AB故：BC=4.83cm；匀变速直线运动中，平均速度等于中间时刻的瞬时速度，故：=0.383m/s 考点：探究小车速度随时间变化的规律 ‎10. （1）电火花打点计时器的工作电源是__V的__电源（填“直流”或“交流”），当电源频率为50Hz时，每隔__秒打一个点．‎ ‎（2）某同学在“用打点计时器测速度”的实验中，用打点计时器记录了被小车拖动的纸带的运动情况，在纸带上确定出A、B、C、D、E、F、G共7个计数点．其相邻点间的距离如图所示，每两个相邻的计数点之间的时间间隔为0.10s．‎ - 11 -‎ ‎①若认为某段时间内的平均速度等于这段时间中间时刻的瞬时速度，则打计数点C、E时小车对应的速度分别为：VC=__m/s，VE=__m/s．（保留小数点后两位）‎ ‎②据此可以求出小车从C到E计数点内的加速度为a=__m/s2．‎ ‎【答案】 (1). 220 (2). 交流 (3). 0.02 (4). 0.48 (5). 0.64 (6). 0.8‎ ‎【解析】（1）电火花打点计时器的工作电源是的交流电源，当电源频率为时，每隔打一个点。‎ ‎（2）①每两个相邻的测量点之间的时间间隔，根据匀变速直线运动中时间中点的速度等于该过程中的平均速度，得： ‎ ‎。‎ ‎②根据匀变速直线运动的推论公式可以求出加速度的大小，‎ 得：， ，‎ 为了更加准确的求解加速度，我们对三个加速度取平均值得：‎ ‎，即小车运动的加速度计算表达式为：。‎ 点睛：对于基本仪器的使用和工作原理，我们不仅从理论上学习它，还要从实践上去了解它，自己动手去做做，以加强基本仪器的了解和使用，要学会应用匀变速直线的规律以及推论解答实验问题的能力，在平时练习中要加强基础知识的理解与应用。‎ ‎11. 甲车以10m/s的速度在平直的公路上匀速行驶，乙车以4m/s的速度与甲车同向做匀速直线运动，甲车经过乙车旁边开始以0.5m/s2的加速度刹车，从甲车刹车开始计时，求：‎ ‎（1）乙车在追上甲车前，两车相距最大的距离．‎ ‎（2）乙车追上甲车所用的时间．‎ ‎【答案】（1）36m（2）25s．‎ ‎【解析】试题分析：（1）在乙车追上甲车之前，当两车速度相等时两车间的距离最大，‎ 设此时经过的时间为t1，则：由v1=v2+at1，得：t1=12s。‎ 此时甲车的位移为：‎ 乙车的位移为：x2=v1t1=4×12m=48m - 11 -‎ 所以两车间的最大距离为：Δx=x2-x1=84m-48m=36m。‎ ‎（2）设甲车停止的时间为t2，则有，‎ 甲车在这段时间内发生的位移为：‎ 乙车发生的位移为x＇=v＇t2=4×20m=80m 则乙车追上甲车所用的时间。‎ 考点：匀变速直线运动的综合运用。‎ ‎【名师点睛】追及、相遇问题的实质 讨论追及、相遇问题，其实质就是分析讨论两物体在相同时间内能否到达相同的空间位置的问题。‎ ‎（1）两个等量关系：即时间关系和位移关系，这两个关系可以通过画草图得到。‎ ‎（2）一个临界条件：即二者速度相等，它往往是物体能否追上、追不上或两者相距最远、最近的临界条件。‎ ‎12. 如图所示，在两车道的公路上有黑白两辆车，黑色车辆停在A线位置，某时刻白色车速度以v1=40m/s通过A线后立即以大小a1=4m/s2的加速度开始制动减速，黑车4s后开始以a2=4m/s2的加速度开始向同一方向匀加速运动，经过一定时间，两车同时 在B线位置．两车看成质点．从白色车通过A线位置开始计时，求经过多长时间两车同时在B线位置及在B线位置时黑色车的速度大小．‎ ‎【答案】40m/s ‎【解析】解：设白车停下来所需的时间为t1，减速过程通过的距离为x1，则υ1=a1t1‎ 解得 x1=200m，t1=10s 在t1=10s时，设黑车通过的距离为x2，则 解得x2=72m＜x1=200m 所以白车停车前未相遇，即白车停车位置就是B线位置．‎ - 11 -‎ 设经过时间t两车同时在B线位置，在B线位置黑车的速度为v2，则 υ2=a2（t﹣t0）‎ 解得t=14s，v2=40m/s 答：经过14s两车同时在B线位置，在B线位置时黑色车的速度大小为40m/s ‎【点评】本题考查运动学中的追及问题，抓住位移和时间关系，运用运动学公式进行求解 ‎（二）选考题 ‎13. 货车A正在该公路上以20m/s的速度匀速行驶，因疲劳驾驶司机注意力不集中，当司机发现正前方有一辆静止的轿车B时，两车距离仅有64m．‎ ‎（1）若此时B车立即以2m/s2的加速度启动，通过计算判断：如果A车司机没有刹车，是否会撞上B车；若不相撞，求两车相距最近时的距离；若相撞，求出从A车发现B车开始到撞上B车的时间．‎ ‎（2）若A车司机发现B车，立即刹车（不计反应时间）做匀减速直线运动，加速度大小为2m/s2（两车均视为质点），为避免碰撞，在A车刹车的同时，B车立即做匀加速直线运动（不计反应时间），问：B车加速度a2至少多大才能避免事故．（这段公路很窄，无法靠边让道）‎ ‎【答案】（1）4s；（2）1.125m/s2 ‎ ‎【解析】解：（1）当两车速度相等时，所用时间为：‎ 在此10s内A车的位移为：‎ xA=vAt=20×10m=200m B车的位移为：‎ 此时AB两车间的位移差为：‎ ‎△x=xA﹣xB=100m＞64m 所以两车必定相撞．‎ 令两车相撞的时间为t，则有相撞时有：‎ 代入数据解得：t=4s（另一根不合题意舍去）‎ 所以A车撞上B车的时间为4s．‎ - 11 -‎ ‎（2）已知A车的加速度，初速度v=20m/s 设B车的加速度为aB，B车运动经过时间t，‎ 两车相遇时，则有：‎ 代入数据有：…①‎ 要避免相撞，则式①无实数解，根据数学关系知，‎ 所以B的加速度的最小值为1.125m/s2‎ 答：（1）如果A车司机没有刹车，会撞上B车；从A车发现B车开始到撞上B车的时间为4s；‎ ‎（2）若A车司机发现B车，立即刹车（不计反应时间）做匀减速直线运动，加速度大小为2m/s2（两车均视为质点），为避免碰撞，在A车刹车的同时，B车立即做匀加速直线运动（不计反应时间）B车加速度a2至少1.125m/s2才能避免事故．‎ 考点：匀变速直线运动的位移与时间的关系．‎ 专题：直线运动规律专题．‎ 分析：（1）能否相撞的判定依据是，当B车速度增加得与A车相等时，A车的位移与B车的位移差与两车距离的比较即可．‎ ‎（2）判断依据仍是AB两车速度相等时的位移关系，由位移关系分析求解B车的加速度最小值即可．‎ 点评：追及问题解题关键：①掌握好两个关系：时间关系和位移关系②一个条件：两者速度相等，这往往是能否追上，或两者距离最大、最小的临界条件是分析问题的切入点．‎ ‎14. 高铁列车上有很多制动装置．在每节车厢上装有制动风翼，当风翼完全打开时，可使列车产生a1=0.5m/s2的平均制动加速度．同时，列车上还有电磁制动系统、空气制动系统、摩擦制动系统等．单独启动电磁制动系统，可使列车产生a2=0.7m/s2的平均制动加速度．所有制动系统同时作用，可使列车产生最大为a=3m/s2的平均制动加速度．在一段直线轨道上，列车正以v0=324km/h的速度匀速行驶时，列车长接到通知，前方有一列车出现故障，需要该列车减速停车．列车长先将制动风翼完全打开让高速行驶的列车减速，当车速减小了时，再通过电磁制动系统同时制动．‎ ‎（1）若不再开启其他制动系统，从开始制动到停车，高铁列车行驶的距离是多少？‎ - 11 -‎ ‎（2）若制动风翼完全打开时，距离前车只有2km，那么该列车最迟在距离前车多远处打开剩余的制动装置，才能保证不与前车相撞？‎ ‎【答案】（1）6000m；（2）1220m ‎ ‎【解析】（1）由题意可得 打开制动风翼时，，‎ 在此过程中行驶的距离：； ‎ 再打开电磁制动后，共同作用的加速度为 ‎ 在此过程中行驶的距离：；‎ 高铁列车在此过程中行驶的总距离：‎ ‎（2）设最迟需要在距离前车△x处打开其他制动装置，由题意知，此时减速需要最大制动加速度，即，，减速之前有：‎ 由以上两式可解得：。‎ 点睛：本题考查匀变速直线运动中追及相遇问题，要注意明确题意，根据已知条件进行分析，从而选择合适的物理规律求解。‎ ‎　‎ ‎ ‎ - 11 -‎