- 542.00 KB
- 2021-04-13 发布
2020届高考数学查漏补缺之选择题题型专练(四)
1、已知集合.则中元素的个数为( )
A.9 B.8 C.5 D.4
2、已知,是虚数单位,若,,则 ( )
A. 或 B. 或 C. D.
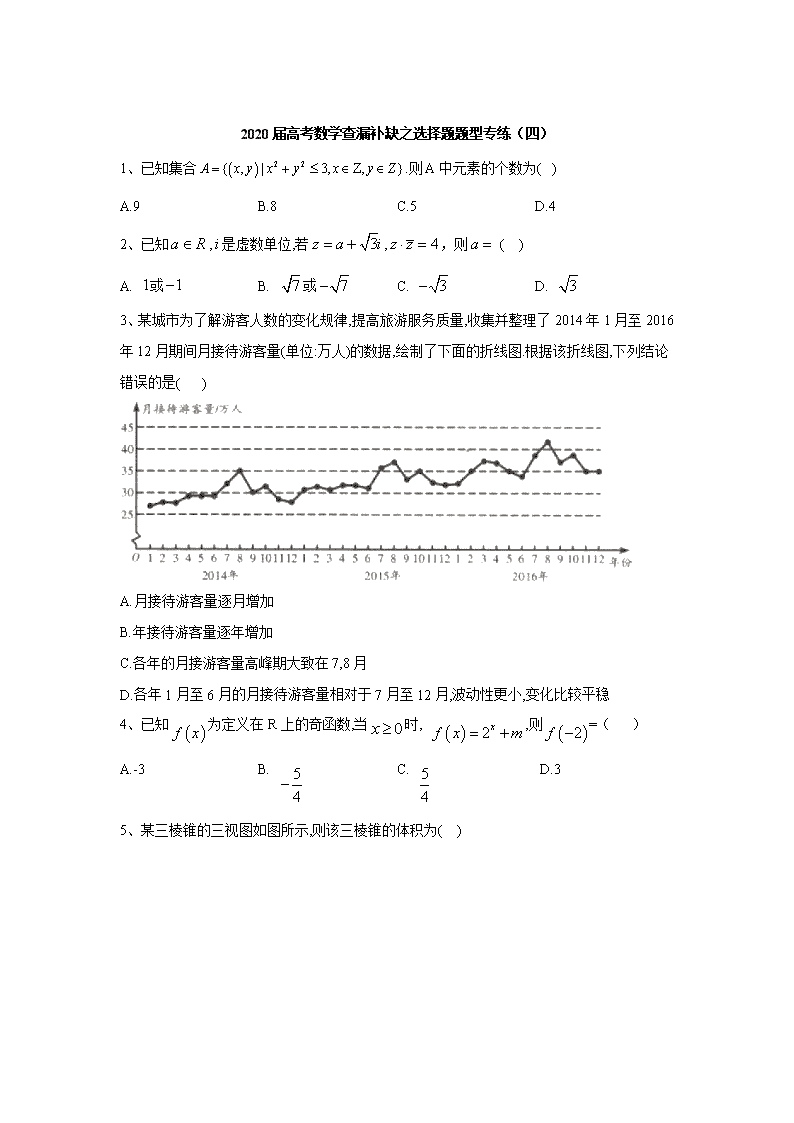
3、某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是( )
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
4、已知为定义在R上的奇函数,当时, ,则=( )
A.-3 B. C. D.3
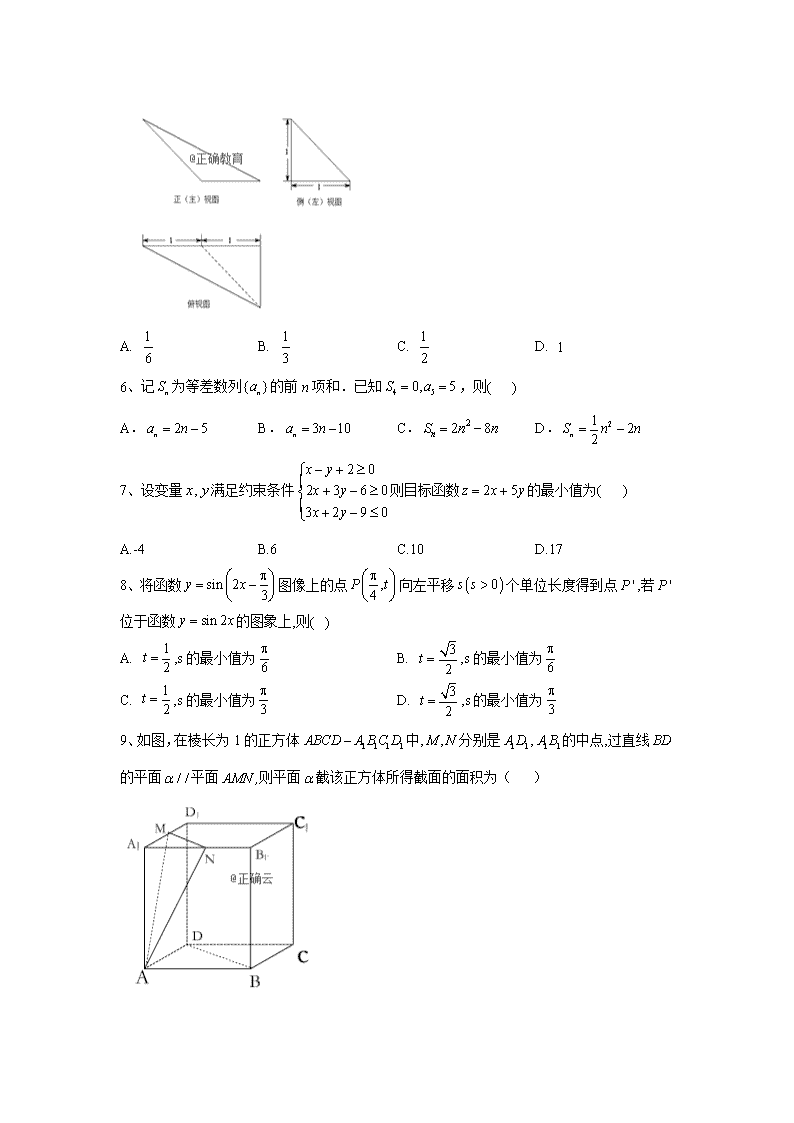
5、某三棱锥的三视图如图所示,则该三棱锥的体积为( )
A. B. C. D.
6、记为等差数列的前n项和.已知,则( )
A. B. C. D.
7、设变量满足约束条件则目标函数的最小值为( )
A.-4 B.6 C.10 D.17
8、将函数图像上的点向左平移个单位长度得到点,若位于函数的图象上,则( )
A. ,s的最小值为 B. ,s的最小值为
C. ,s的最小值为 D. ,s的最小值为
9、如图,在棱长为1的正方体中,分别是,的中点,过直线的平面平面,则平面截该正方体所得截面的面积为( )
A. B. C. D.
10、已知函数(,且)在上单调递减,且关于的方程恰好有两个不相等的实数解,则的取值范围是( )
A. B. C. D.
11、已知椭圆的左、右焦点分别为,左、右顶点分别为,过的直线交于两点(异于),的周长为,且直线与的斜率之积为,则的方程为( )
A. B. C. D.
12、若函数(是自然对数的底数)在的定义域上单调递增,则称函数具有M性质,下列函数中具有M性质的是( )
A. B. C. D.
答案以及解析
1答案及解析:
答案:A
解析:因为:
所以:
因为:
所以:
当时,
当时, ;
当时, ;
所以共有9个,选A.
2答案及解析:
答案:A
解析:由,,得,所以,故选A.
3答案及解析:
答案:A
解析:A项,由折线图可看出2014年9月接待的游客量小于8月接待的游客量,因此月接待游客量并不是逐月增加的,故A项结论错误符合题意.
B项,由折线图可看出2014年每个月接待的游客量小于2015年对应月份接待的游客量,2015年每个月接待的游客量小于2016年对应月份接待的游客量,所以年接待游客量逐年增加,故B项不符合题意.
C项,由折线图可看出每一年的7,8月接待的游客量远高于当年其他月份,因此各年的月接待游客量高峰期大致在7,8月,故C项不符合题意.
D项,由折线图可看出各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳,故D项不符合题意.
故本题正确答案为A.
4答案及解析:
答案:A
解析:函数为奇函数,则,
∴,
结合奇函数的性质可知:.
5答案及解析:
答案:A
解析:分析三视图可知,该几何体为—三棱锥,其体积,故选A.
6答案及解析:
答案:A
解析:由题知,,解得,∴,故选A.
7答案及解析:
答案:B
解析:可行域为一个三角形及其内部,其中,直线过点时取最小值6,选B
8答案及解析:
答案: A
解析:由题意得, ,
故所对应的点为,
此时向左平移个单位,故选A
9答案及解析:
答案:B
解析:取的中点E,的中点F,连接EF,BE,DF, ,则EF∥,∥BD,所以EF∥BD,故EFBD在同一平面内,
连接ME,因为M,E分别为的中点,
所以ME∥AB,且ME=AB,
所以四边形ABEM是平行四边形,
所以AM∥BE,又因为BE⊂平面BDFE,AM不在平面BDFE内,
所以AM∥平面BDFE,
同理AN∥平面BDFE,
因为AM∩AN=A,
所以平面AMN∥平面BDFE,
即平面a截该正方体所得截面为平面BDFE
梯形BDFE如图:
过E,F作BD的垂线,则四边形EFGH为矩形,
∴
故四边形BDFE的面积为
故选:B.
10答案及解析:
答案:C
解析:由在上递减可知,由方程恰好有两个不相等的实数解,可知,,又∵时,抛物线与直线相切,也符合题意,∴实数的去范围是,故选C.
11答案及解析:
答案:C
解析:由的周长为,可知.
解得,则.
设点,由直线AM与AN的斜率之积为,可得.即.①
又,所以,②
由①②解得:.
所以椭圆C的方程为.故选C.
12答案及解析:
答案:A
解析:对于选项A,,则,∵,∴在R上单调递增,∴具有M性质.对于选项B,,令,得或;令,得,∴函数在和上单调递增,在上单调递减,∴不具有M性质.对于选项C,,则,∵,∴在R上单调递减,∴
不具有M性质.对于选项D,,则在R上不恒成立,故在R上不是单调递增的,所以不具有M性质.