- 630.50 KB
- 2021-04-13 发布
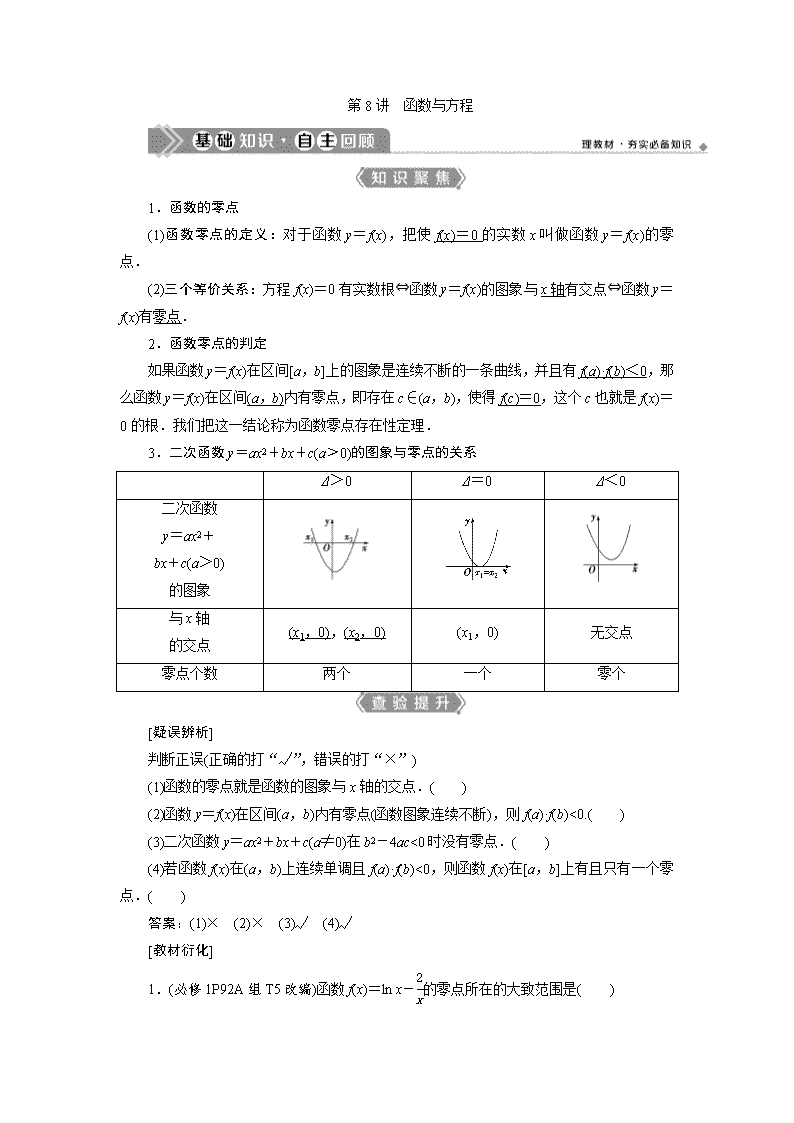
第 8 讲 函数与方程
1.函数的零点
(1)函数零点的定义:对于函数 y=f(x),把使 f(x)=0 的实数 x 叫做函数 y=f(x)的零
点.
(2)三个等价关系:方程 f(x)=0 有实数根⇔函数 y=f(x)的图象与 x 轴有交点⇔函数 y=
f(x)有零点.
2.函数零点的判定
如果函数 y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有 f(a)·f(b)<0,那
么函数 y=f(x)在区间(a,b)内有零点,即存在 c∈(a,b),使得 f(c)=0,这个 c 也就是 f(x)=
0 的根.我们把这一结论称为函数零点存在性定理.
3.二次函数 y=ax2+bx+c(a>0)的图象与零点的关系
Δ>0 Δ=0 Δ<0
二次函数
y=ax2+
bx+c(a>0)
的图象
与 x 轴
的交点
(x1,0),(x2,0) (x1,0) 无交点
零点个数 两个 一个 零个
[疑误辨析]
判断正误(正确的打“√”,错误的打“×”)
(1)函数的零点就是函数的图象与 x 轴的交点.( )
(2)函数 y=f(x)在区间(a,b)内有零点(函数图象连续不断),则 f(a)·f(b)<0.( )
(3)二次函数 y=ax2+bx+c(a≠0)在 b2-4ac<0 时没有零点.( )
(4)若函数 f(x)在(a,b)上连续单调且 f(a)·f(b)<0,则函数 f(x)在[a,b]上有且只有一个零
点.( )
答案:(1)× (2)× (3)√ (4)√
[教材衍化]
1.(必修 1P92A 组 T5 改编)函数 f(x)=ln x-
2
x的零点所在的大致范围是( )
A.(1,2) B.(2,3)
C.(1
e,1 )和(3,4) D.(4,+∞)
解析:选 B.易知 f(x)为增函数,由 f(2)=ln 2-1<0,f(3)=ln 3-2
3>0,得 f(2)·f(3)<0.
故选 B.
2.(必修 1P88 例 1 改编)函数 f(x)=ex+3x 的零点个数是______.
解析:由已知得 f′(x)=ex+3>0,所以 f(x)在 R 上单调递增,又 f(-1)=
1
e-3<0,f(0)=
1>0,因此函数 f(x)有且只有一个零点.
答案:1
[易错纠偏]
(1)错用零点存在性定理;
(2)误解函数零点的定义;
(3)忽略限制条件;
(4)错用二次函数在 R 上无零点的条件.
1.函数 f(x)=x+
1
x的零点个数是______.
解析:函数的定义域为{x|x≠0},当 x>0 时,f(x)>0,当 x<0 时,f(x)<0,所以函数没有
零点.
答案:0
2.函数 f(x)=x2-3x 的零点是______.
解析:由 f(x)=0,得 x2-3x=0,
即 x=0 和 x=3.
答案:0 和 3
3.若二次函数 f(x)=x2-2x+m 在区间(0,4)上存在零点,则实数 m 的取值范围是______.
解析:二次函数 f(x)图象的对称轴方程为 x=1.若在区间(0,4)上存在零点,只需 f(1)≤0
且 f(4)>0 即可,即-1+m≤0 且 8+m>0,解得-80,所以 f(1
4 )·f(1
2 )<0,故函数 f(x)=πx+log2x 的零点所在
区间为[1
4,
1
2 ].
2.(2020·杭州市严州中学高三模拟)若 a0,f(b)<0,f(c)>0,
所以 f(x)的两个零点分别位于区间(a,b)和(b,c)内.
函数零点个数的问题
(1)函数 f(x)={x2+x-2,x ≤ 0,
-1+ln x,x > 0 的零点个数为( )
A.3 B.2
C.1 D.0
(2)已知函数 f(x)满足 f(x)=f(3x),且当 x∈[1,3)时,f(x)=ln x,若在区间[1,9)内,函
数 g(x)=f(x)-ax 有三个不同的零点,则实数 a 的取值范围是( )
A.(ln 3
3 ,
1
e) B.(ln 3
9 ,
1
3e)
C.(ln 3
9 ,
1
2e) D.(ln 3
9 ,
ln 3
3 )
【解析】 (1)法一:由 f(x)=0 得{x ≤ 0,
x2+x-2=0
或{x > 0,
-1+ln x=0,解得 x=-2 或 x=e.
因此函数 f(x)共有 2 个零点.
法二:函数 f(x)的图象如图所示,
由图象知函数 f(x)共有 2 个零点.
(2)因为 f(x)=f(3x)⇒f(x)=f (x
3 ),当 x∈[3,9)时,f(x)=f (x
3 )=ln
x
3,所以 f(x)=
{ln x,1 ≤ x < 3,
ln
x
3,3 ≤ x < 9, 而 g(x)=f(x)-ax 有三个不同零点⇔y=f(x)与 y=ax 的图象有三个不
同交点,如图所示,可得直线 y=ax 应在图中两条虚线之间,所以可解得
ln 3
9 0),y2=ln x(x>0)的图象,如图所示.
由图可知函数 f(x)在定义域内的零点个数为 2.
2.已知函数 f(x)是定义在(-∞,0)∪(0,+∞)上的偶函数,当 x>0 时,f(x)=
{2|x-1|-1,0 < x ≤ 2,
1
2f(x-2),x > 2, 则函数 g(x)=4f(x)-1 的零点个数为( )
A.4 B.6
C.8 D.10
解析:选 D.由 f(x)为偶函数可得,只需作出 x∈(0,+∞)上的
图象,再利用对称性作另一半图象即可.当 x∈(0,2]时,可以通过
y=2x 的图象进行变换作出 f(x)的图象,当 x>2 时,f(x)=
1
2f(x-2),
即自变量差 2 个单位,函数值折半,进而可作出 f(x)在(2,4],(4,
6],…的图象,如图所示.g(x)的零点个数即 f(x)=
1
4的根的个数,也即 f(x)的图象与 y=
1
4的
图象的交点个数,观察图象可知,当 x>0 时,有 5 个交点,根据对称性可得当 x<0 时,也有 5
个交点,共计 10 个交点,故选 D.
函数零点的应用(高频考点)
高考对函数零点的考查多以选择题或填空题的形式出现.主要命题角度有:
(1)利用函数零点比较大小;
(2)已知函数的零点(或方程的根)的情况求参数的值或范围;
(3)利用函数零点的性质求参数的范围.
角度一 利用函数零点比较大小
(2020·台州模拟)已知 e 是自然对数的底数,函数 f(x)=ex+x-2 的零点为 a,函数
g(x)=ln x+x-2 的零点为 b,则下列不等式中成立的是( )
A.f(a)0 恒成立,所以函数 f(x)在 R 上是单调递增的,而 f(0)
=e0+0-2=-1<0,f(1)=e1+1-2=e-1>0,所以函数 f(x)的零点 a∈(0,1);
由题意,知 g′(x)=
1
x+1>0,所以函数 g(x)在(0,+∞)上是单调递增的,又 g(1)=ln 1+
1-2=-1<0,g(2)=ln 2+2-2=ln 2>0,所以函数 g(x)的零点 b∈(1,2).
综上,可得 04.
【答案】 (1)[log2
1
3,log2
3
5] (2)(1,4) (1,3]∪(4,+∞)
角度三 利用函数零点的性质求参数的范围
已知函数 f(x)=|ln x|,若 00),由
00,从而{ln a=-t,
ln b=t, 即{a=e-t,
b=et, 所以 a+
2b=
1
et+2et,而 et>1,又 y=2x+
1
x在(1,+∞)上为增函数,所以 2et+
1
et∈(3,+∞).故选 C.
【答案】 C
已知函数的零点(或方程根)的情况求
参数问题常用的三种方法
(1)直接法:直接根据题设条件构建关于参数的不等式,再通过解不等式确定参数范
围.
(2)分离参数法:先将参数分离,转化成求函数值域问题加以解决.
(3)数形结合法:先对解析式变形,在同一平面直角坐标系中画出函数的图象,然后数
形结合求解.
1.(2019·高考浙江卷)设 a,b∈R,函数 f(x)={x,x < 0,
1
3x3-1
2(a+1)x2+ax,x ≥ 0.若函数
y=f(x)-ax-b 恰有 3 个零点,则( )
A.a<-1,b<0 B.a<-1,b>0
C.a>-1,b<0 D.a>-1,b>0
解析:选 C.由题意可得,当 x≥0 时,f(x)-ax-b=
1
3x3-
1
2(a+1)x2-b,令 f(x)-ax-b=
0,则 b=
1
3x3-
1
2(a+1)x2=
1
6x2[2x-3(a+1)].因为对任意的 x∈R,f(x)-ax-b=0 有 3 个不
同的实数根,所以要使满足条件,则当 x≥0 时,b=
1
6x2[2x-3(a+1)]必须有 2 个零点,所以
3(a+1)
2 >0,解得 a>-1.所以 b<0.故选 C.
2.已知函数 f(x)={log2(x+1),x>0,
-x2-2x,x ≤ 0, 若函数 g(x)=f(x)-m 有 3 个零点,则实数 m
的取值范围是________.
解析:函数 g(x)=f(x)-m 有 3 个零点,转化为 f(x)-m=0 的根有 3 个,进而转化为 y=
f(x),y=m 的交点有 3 个.画出函数 y=f(x)的图象,则直线 y=m 与其有 3 个公共点.又抛
物线顶点为(-1,1),由图可知实数 m 的取值范围是(0,1).
答案:(0,1)
3.(2020·杭州学军中学高三质检)若函数 f(x)=|2x-1|+ax-5(a 是常数,且 a∈R)恰有
两个不同的零点,则 a 的取值范围为________.
解析:由 f(x)=0,得|2x-1|=-ax+5.
作出 y=|2x-1|和 y=-ax+5 的图象,观察可以知道,当-20,f(3)<0,f(4)>0,f(5)<0,根据零点存在性定理可知,f(x)在
区间(2,3),(3,4),(4,5)上均至少含有一个零点,故函数 y=f(x)在区间[1,6]上的零点至
少有 3 个.
2.(2020·温州十校联考(一))设函数 f(x)=ln x+x-2,则函数 f(x)的零点所在的区间为
( )
A.(0,1) B.(1,2)
C.(2,3) D.(3,4)
解析:选 B.法一:因为 f(1)=ln 1+1-2=-1<0,f(2)=ln 2>0,所以 f(1)·f(2)<0,因为
函数 f(x)=ln x+x-2 的图象是连续的,所以函数 f(x)的零点所在的区间是(1,2).
法二:函数 f(x)的零点所在的区间为函数 g(x)=ln x,h(x)=-x+2 图象
交点的横坐标所在的区间,作出两函数的图象如图所示,由图可知,函数
f(x)的零点所在的区间为(1,2).
3.已知函数 f(x)=(1
2 ) x
-cos x,则 f(x)在[0,2π]上的零点个数为
( )
A.1 B.2
C.3 D.4
解析:选 C.作出 g(x)=(1
2 ) x
与 h(x)=cos x 的图象如图所
示,可以看到其在[0,2π]上的交点个数为 3,所以函数 f(x)在[0,
2π]上的零点个数为 3,故选 C.
4.已知函数 f(x)=(1
e ) x
-tan x(-π
2 < x <
π
2 ),若实数 x0 是函数 y=f(x)的零点,
且 0f(x0)=0.故选 B.
5.(2020·兰州模拟)已知奇函数 f(x)是 R 上的单调函数,若函数 y=f(2x2+1)+f(λ-x)只
有一个零点,则实数 λ 的值是( )
A.
1
4 B.
1
8
C.-
7
8 D.-
3
8
解析:选 C.因为函数 y=f(2x2+1)+f(λ-x)只有一个零点,所以方程 f(2x2+1)+f(λ-x)=
0 只有一个实数根,又函数 f(x)是定义在 R 上的奇函数,所以 f(-x)=-f(x),所以 f(2x 2+1)+
f(λ-x)=0⇔f(2x2+1)=-f(λ-x)⇔f(2x2+1)=f(x-λ)⇔2x2+1=x-λ,所以方程 2x2-x+1+λ
=0 只有一个实数根,所以 Δ=(-1)2-4×2×(1+λ)=0,解得 λ=-
7
8.故选 C.
6.(2020·宁波市余姚中学期中检测)已知函数 f(x)=
|x|
x+2-kx2(k∈R)有四个不同的零点,
则实数 k 的取值范围是( )
A.k<0 B.k<1
C.01
解析:选 D.分别画出 y=
|x|
x+2与 y=kx2 的图象如图所示,
当 k<0 时,y=kx2 的开口向下,此时与 y=
|x|
x+2只有一个交点,显然不符合题意;
当 k=0 时,此时与 y=
|x|
x+2只有一个交点,显然不符合题意,
当 k>0,x≥0 时,
令 f(x)=
|x|
x+2-kx2=0,
即 kx3+2kx2-x=0,
即 x(kx2+2kx-1)=0,
即 x=0 或 kx2+2kx-1=0,
因为 Δ=4k2+4k>0,且-
1
k<0,所以方程有一正根,一负根,所以当 x>0 时,方程有唯
一解.即当 x≥0 时,方程有两个解.
当 k>0,x<0 时,f(x)=
|x|
x+2-kx2=0,
即 kx3+2kx2+x=0,kx2+2kx+1=0,
此时必须有两个解才满足题意,所以Δ=4k2-4k>0,解得 k>1,
综上所述 k>1.
7.(2020·金丽衢十二校高三联考)设函数 f(x)={tan[
π
2 (x-1)],0 < x ≤ 1
ln x,x > 1
,则 f(f(e))=
________,函数 y=f(x)-1 的零点为________.
解析:因为 f(x)={tan[
π
2 (x-1)],0 < x ≤ 1
ln x,x > 1
,
所以 f(e)=ln e=1,
f(f(e))=f(1)=tan 0=0,
若 01,f(x)=1⇒ln x=1⇒x=e.
答案:0 e
8.已知函数 f(x)=
2
3x+1+a 的零点为 1,则实数 a 的值为________.
解析:由已知得 f(1)=0,即 2
31+1+a=0,解得 a=-
1
2.
答案:-
1
2
9.已知函数 f(x)= {2x,x ≤ 0,
|log2x|,x > 0,则函数 g(x)=f(x)-
1
2的零点所构成的集合为
________.
解析:令 g(x)=0,得 f(x)=
1
2,所以{x ≤ 0,
2x=1
2
或{x > 0,
|log2x|=1
2,解得 x=-1 或 x=
2
2 或
x= 2,故函数 g(x)=f(x)-
1
2的零点所构成的集合为{-1,
2
2 , 2}.
答案:{-1,
2
2 , 2}
10.(2020·杭州学军中学模拟)已知函数 f(x)=|x 3-4x|+ax-2 恰有 2 个零点,则实数 a
的取值范围为________.
解析:函数 f(x)=|x3-4x|+ax-2 恰有 2 个零点即函数 y=|x3-
4x|与 y=2-ax 的图象有 2 个不同的交点.作出函数 y=|x3-4x|的图
象如图,当直线 y=2-ax 与曲线 y=-x3+4x,x∈[0,2]相切时,
设切点坐标为(x0,-x30+4x0),则切线方程为 y-(-x30+4x0)=(-3x
20+4)(x-x0),且经过点(0,2),代入解得 x0=1,此时 a=-1,由
函数图象的对称性可得实数 a 的取值范围为 a<-1 或 a>1.
答案:a<-1 或 a>1
11.设函数 f(x)=ax2+bx+b-1(a≠0).
(1)当 a=1,b=-2 时,求函数 f(x)的零点;
(2)若对任意 b∈R,函数 f(x)恒有两个不同零点,求实数 a 的取值范围.
解:(1)当 a=1,b=-2 时,f(x)=x2-2x-3,令 f(x)=0,得 x=3 或 x=-1.
所以函数 f(x)的零点为 3 和-1.
(2)依题意,f(x)=ax2+bx+b-1=0 有两个不同实根,所以 b2-4a(b-1)>0 恒成立,即
对于任意 b∈R,b2-4ab+4a>0 恒成立,所以有(-4a)2-4×(4a)<0⇒a2-a<0,解得 0 0) ,则下列关于函数
y=f[f(kx)+1]+1(k≠0)的零点个数的判断正确的是( )
A.当 k>0 时,有 3 个零点;当 k<0 时,有 4 个零点
B.当 k>0 时,有 4 个零点;当 k<0 时,有 3 个零点
C.无论 k 为何值,均有 3 个零点
D.无论 k 为何值,均有 4 个零点
解析:选 C.令 f[f(kx)+1]+1=0 得,
{f(kx)+1 ≤ 0,
ef(kx)+1-2+1=0或{f(kx)+1 > 0
ln[f(kx)+1]+1=0,
解得 f(kx)+1=0 或 f(kx)+1=
1
e;
由 f(kx)+1=0 得,
{kx ≤ 0,
ekx-2+1=0或{kx > 0
ln(kx)=-1;
即 x=0 或 kx=
1
e;
由 f(kx)+1=
1
e得,
{kx ≤ 0,
ekx-2+1=1
e
或{kx > 0
ln(kx)+1=1
e
;
即 ekx=1+
1
e(无解)或 kx=e
1
e-1;
综上所述,x=0 或 kx=
1
e或 kx=e
1
e-1;
故无论 k 为何值,均有 3 个解,故选 C.
2.(2020·宁波市高三教学评估)设函数 f(x)=ax 2+bx+c(a,b,c∈R 且 a>0),则“f
(f(- b
2a ))<0”是“f(x)与 f(f(x))都恰有两个零点”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
解析:选 C.由已知 a>0,函数 f(x)开口向上,f(x)有两个零点,最小值必然小于 0,当取
得最小值时,x=-
b
2a,即 f(- b
2a )<0,令 f(x)=-
b
2a,则 f(f(x))=f(- b
2a ),因为 f(- b
2a )<0,
所以 f(f(x))<0,所以 f(f(x))必有两个零点.同理 f(f( b
2a ))<0⇒f(- b
2a )<0⇒x=-
b
2a,因为 x=
-
b
2a是对称轴,a>0,开口向上,f(- b
2a )<0,必有两个零点所以 C 选项正确.
3.(2020·瑞安市龙翔高中高三月考)若关于 x 的不等式 x2+|x-a|<2 至少有一个正数解,
则实数 a 的取值范围是________.
解析:不等式为 2-x2>|x-a|,则 0<2-x2.
在同一坐标系画出 y=2-x2(y≥0,x≥0)和 y=|x|两个函数图
象,将绝对值函数 y=|x|向左移动,当右支经过(0,2)点时,a=-
2;将绝对值函数 y=|x|向右移动让左支与抛物线 y=2-x2(y≥0,x
≥0)相切时,
由{y-0=-(x-a)
y=2-x2 ,可得 x2-x+a-2=0,
再由 Δ=0 解得 a=
9
4.
数形结合可得,实数 a 的取值范围是(-2,
9
4).
答案:(-2,
9
4)
4.已知函数 f(x)=(1
2 ) x
,g(x)=log
1
2
x,记函数 h(x)={g(x),f(x) ≤ g(x),
f(x),f(x) > g(x),
则函数 F(x)=h(x)+x-5 的所有零点的和为________.
解析:由题意知函数 h(x)的图象如图所示,易知函数 h(x)的
图象关于直线 y=x 对称,函数 F(x)所有零点的和就是函数 y=h(x)
与函数 y=5-x 图象交点横坐标的和,设图象交点的横坐标分别
为 x1,x2,因为两函数图象的交点关于直线 y=x 对称,所以
x1+x2
2 =
5-x1+x2
2 ,所以 x1+x2=5.
答案:5