2019-2020学年江西省吉安市永丰中学高二上学期期中考试数学（文）试题 Word版 9页

永丰中学2019-2020学年第一学期高二年级期中考试 数学（文科）试卷 时间：120分钟 总分：150分 一、选择题（本大题共有12小题，每题5分，共60分）‎ ‎1．关于下列几何体，说法正确的是（　　）‎ A．图①是圆柱 B．图②和图③是圆锥 C．图④和图⑤是圆台 D．图⑤是圆台 ‎2．垂直于同一条直线的两条直线一定（　　）‎ A．平行 B．相交 C．异面 D．以上都有可能 ‎3．下列命题错误的是（ ） ‎ A．命题“若，则”的逆否命题为“若中至少有一个不为则”‎ B．若命题，则 C．中，是的充要条件 D．若向量满足，则与的夹角为钝角 ‎4．已知直线的斜率，则直线的倾斜角的范围是（　　）‎ A． B． C． D．‎ ‎5．若点在圆的内部，则实数a的取值范围是（ ）‎ A． B． C．或 D．‎ ‎6．已知直线：平行于直线：，且在y轴上的截距为，则的值分别为(　　)‎ A．4,3 B．－4,‎3 C．－4,－3 D．4，－3‎ ‎7．如图，在正方体中，M， N分别为棱的中点，以下四个结论：①直线DM与是相交直线；②直线AM与NB是平行直线；③直线BN与是异面直线；④直线AM与是异面直线．其中正确的个数为（ ）‎ A．1 B．‎2 ‎C．3 D．4‎ ‎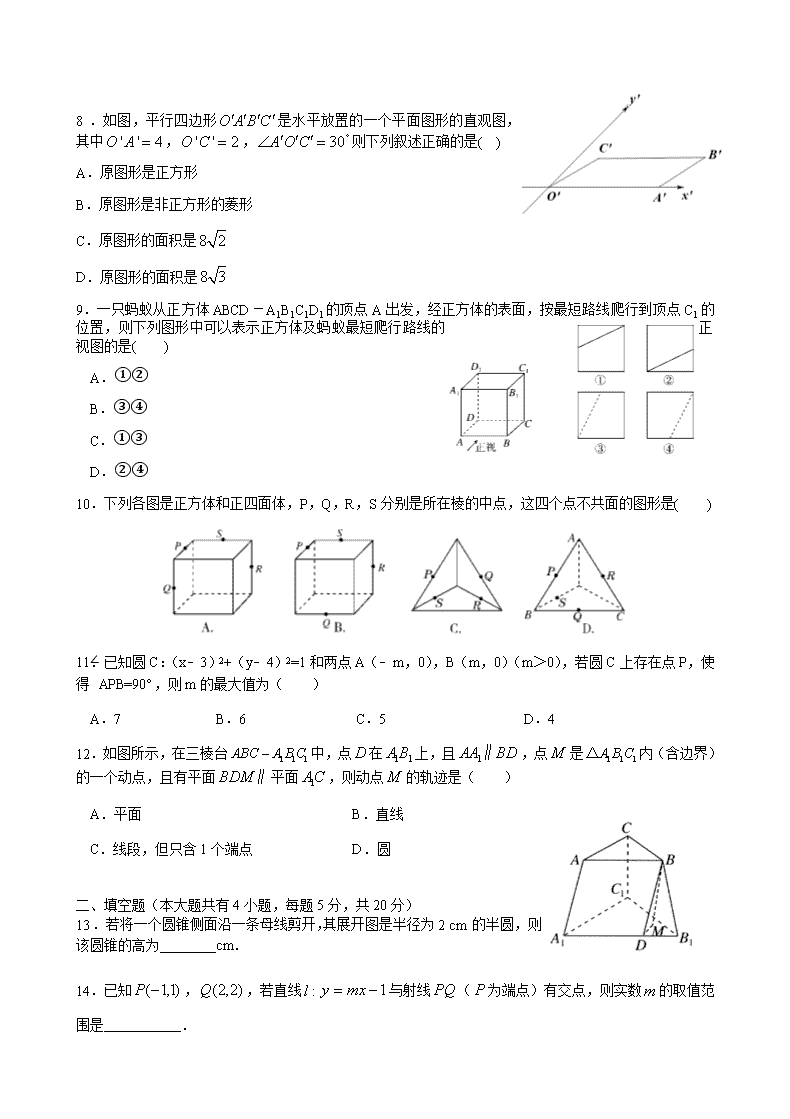8．如图，平行四边形是水平放置的一个平面图形的直观图，其中，，则下列叙述正确的是( )‎ A．原图形是正方形 ‎ B．原图形是非正方形的菱形 C．原图形的面积是 ‎ D．原图形的面积是 ‎9．一只蚂蚁从正方体ABCD－A1B‎1C1D1的顶点A出发，经正方体的表面，按最短路线爬行到顶点C1的位置，则下列图形中可以表示正方体及蚂蚁最短爬行路线的正视图的是(　　)‎ A．①② ‎ B．③④‎ C．①③ ‎ D．②④‎ ‎10．下列各图是正方体和正四面体，P，Q，R，S分别是所在棱的中点，这四个点不共面的图形是(　　)‎ ‎ ‎ ‎11．已知圆C：（x﹣3）2+（y﹣4）2=1和两点A（﹣m，0），B（m，0）（m＞0），若圆C上存在点P，使得∠APB=90°，则m的最大值为（　　）‎ A．7 B．‎6 ‎ C．5 D．4‎ ‎12．如图所示，在三棱台中，点在上，且，点是内（含边界）的一个动点，且有平面平面，则动点的轨迹是（ ）‎ A．平面 B．直线 ‎ C．线段，但只含1个端点 D．圆 二、填空题（本大题共有4小题，每题5分，共20分）‎ ‎13．若将一个圆锥侧面沿一条母线剪开，其展开图是半径为2 cm的半圆，则该圆锥的高为________cm．‎ ‎14．已知，，若直线与射线（为端点）有交点，则实数的取值范围是 ．‎ ‎15．如图，已知正三棱柱的底面边长为2，高为5，一质点自A点出发，沿着三棱柱的侧面绕行两周到达A1点的最短路线的长为________．‎ ‎16．点M（x，y）在函数的图象上，则的取值范围是　　．‎ 三、解答题（本大题共有6小题，其中第17题10分，其他题每题12分，共70分）‎ ‎17．（本小题10分）‎ 一条光线从点M（2，3）射出，遇轴反射后经过N（-1， 6），求入射光线所在直线方程。‎ ‎18．（本小题12分）‎ 如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，底面ABCD是菱形，点O是对角线AC与BD的交点，M是PD的中点．‎ ‎（1）求证：OM∥平面PAB； ‎ ‎（2）求证：平面PBD⊥平面PAC．‎ ‎19．（本小题12分）‎ 直三棱柱ABC﹣A1B‎1C1的底面为等腰直角三角形，∠BAC=90°，AB=AC=2，，E，F分别是BC，AA1的中点．‎ 求:（1）异面直线EF和A1B所成的角．‎ ‎（2）三棱锥A﹣EFC的体积．‎ ‎20．（本小题12分）‎ 设命题p：实数x满足，其中；命题q：．‎ ‎（1）若，且为真，求实数x的取值范围；‎ ‎（2）若是的充分不必要条件，求实数m的取值范围．‎ ‎21．（本小题12分）‎ 已知圆：与直线：，动直线过定点．‎ ‎（1）若直线与圆相切，求直线的方程；‎ ‎（2）若直线与圆相交于、两点，点M是PQ的中点，直线与直线相交于点N．探索是否为定值，若是，求出该定值；若不是，请说明理由．‎ ‎22.（本小题12分）‎ 已知点B（－1，0），C（1，0），P是平面上一动点，且满足 ‎（1）求点P的轨迹C对应的方程；‎ ‎（2）已知点A（n，2）在曲线C上，过点A作曲线C的两条弦AD和AE，且AD⊥AE，判断：直线DE是否过定点？试证明你的结论．‎ 永丰中学2019-2020学年上学期高二年级期中考试 数学（文科）参考答案 一、选择题：（本大题共有12小题，每题5分，共60分）‎ ‎1．D 2．D 3.D 4．C 5．A 6．C 7．C 8．C 9．.D 10．D 11．B 12．C 二、填空题：（本大题共有4小题，每题5分，共20分）‎ ‎13． 14． 15．13 16．．‎ 三、解答题：（本大题共有6小题，其中第17题10分，其他题每题12分，共70分）‎ ‎17．解：设入射光线与轴的交点为P（），则直线MP的倾斜角与直线NP的倾斜角互补，‎ ‎ 则 ……3分 ‎ ‎ ‎ …………6分 ‎ ‎ ‎ 直线MP的方程为 ‎ 即 …………10分 ‎18．证明：（1）∵在△PBD中，O、M分别是BD、PD的中点，‎ ‎∴OM是△PBD的中位线，∴OM∥PB，‎ ‎∵OM⊄平面PAB，PB⊂平面PAB，‎ ‎∴OM∥平面PAB；‎ ‎（2）∵底面ABCD是菱形，∴BD⊥AC，‎ ‎∵PA⊥平面ABCD，BD⊂平面ABCD，∴BD⊥PA．‎ ‎∵AC⊂平面PAC，PA⊂平面PAC，AC∩PA=A，∴BD⊥平面PAC，‎ ‎∵BD⊂平面PBD，‎ ‎∴平面PBD⊥平面PAC．‎ ‎19．【解答】解：（1）取AB的中点D，连DE、DF，则DF∥A1B，‎ ‎∴∠DFE（或其补角）即为所求．‎ 由题意易知，，DE=1，‎ 由DE⊥AB、DE⊥AA1得DE⊥平面ABB‎1A1‎ ‎∴DE⊥DF，即△EDF为直角三角形，∴，∴∠DFE=30°‎ 即异面直线EF和A1B所成的角为30°．‎ ‎（2）VA﹣EFC=VF﹣AEC﹣=．‎ ‎20．解：(1)由，其中；‎ 解得，‎ 又，即， 由得：， 又为真，则，‎ 得：， 故实数x的取值范围为；‎ 由得：命题p：，命题q：，‎ 由是的充分不必要条件，即p是q的充分不必要条件，‎ 则， 所以，即． 故实数m取值范围为：．‎ ‎21．解：（1）当直线的斜率不存在时， 直线的方程为，此时与圆相切，符合题意；‎ 当直线的斜率存在时， 设直线的方程为，即，‎ 若直线与圆相切，则圆心 到直线的距离等于半径1，‎ 所以，解得 ，‎ 所以直线的方程为，即．‎ 综上，直线的方程为或．‎ 直线的方程为或．‎ ‎（2）∵⊥，‎ ‎∴‎ 若直线与轴垂直时，不符合题意；‎ 所以的斜率存在，设直线的方程为，‎ 则由，即．‎ ‎∴， 从而．‎ 综上所述， ．‎ ‎22、解：（1）设