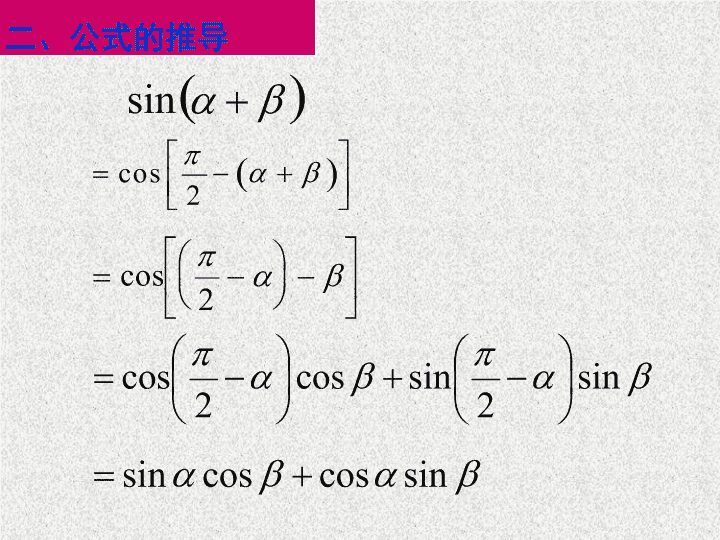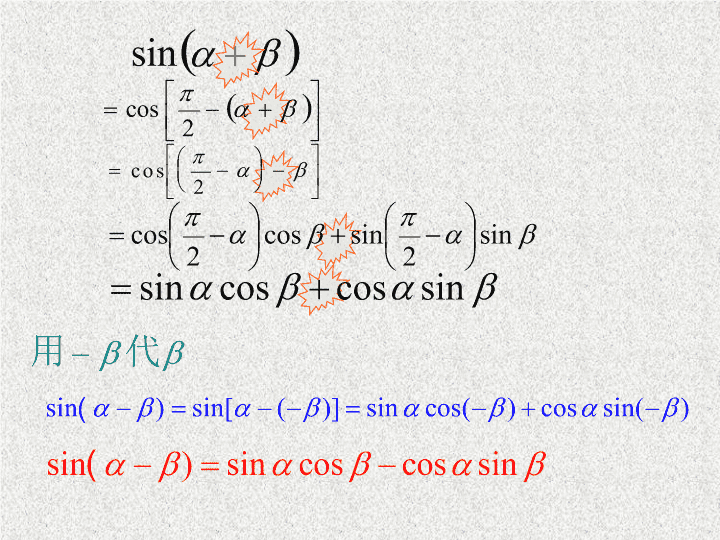2020届二轮复习两角和与差的正弦、余弦、正切公式课件（18张）（全国通用） 18页

一、复习： cos （  + ） =cos  cos  – sin  sin  cos (  –  ） =cos  cos  + sin sin 二、公式的推导 两角和与差的正弦公式 1、两角和的余弦公式 2、两角差的余弦公式 简记： 简记： 两角和的正切公式： 上式中以  代  得 注意： 1  必须在定义域范围内使用上述公式。 2 注意公式的结构，尤其是符号。 即： tan  ， tan ， tan( ±  ) 只要有一个不存在就不能使用这个公式，只能（也只需）用诱导公式来解。如 : 已知 tan  =2, 求 不能用 两角和与差的正切公式 问 : 如何求 cot( a+ β )? 有关两角和差的余切问题，一般都是将它由同角公 式的倒数关系化为两角和差的正切，用公式来解决． 三 、公式应用 1: 求 tan15  和 tan75 的值： 解： tan15  = tan(45  30  )= tan75  = tan(45  +30  )= 四、练习； 2 、化简： 3 、求值： 答案 : 答案 : (1) 1 (2) -1 五 . 小结 变形： 求下列各式的值： (1) (2) tan17  +tan28  +tan17  tan28  解： 1  原式 = 2  ∵ ∴tan17  +tan28  =tan(17  +28  )(1  tan17  tan28  ) =1  tan17  tan28  ∴ 原式 =1  tan17  tan28  + tan17  tan28  =1 引例 把下列各式化为一个角的三角函数形式 化 为一个角的三角函数形式 令 练习 把下列各式化为一个角的三角函数形式