- 716.00 KB
- 2021-04-13 发布
文科数学试题
第Ⅰ卷(选择题 60分)
一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是最符合题目要求的.)
1.设集合,集合,则( ).
A. B. C. D.
2.已知角的顶点与原点重合,始边与轴的非负半轴重合,是角终边上的一点,则的值为( ).
A.3 B. C. D.-3
3.某学校高一、高二、高三年级的学生人数之比为4:3:3,现用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本,则从高二年级抽取的学生人数为( ).
A.15 B.20 C.25 D. 30
4.已知实数满足不等式组,且的最小值为,最大值为,则( ).
A.15 B.16 C.17 D.18
5.已知均为单位向量,它们的夹角为60°,那么( ).
A. B. C.4 D.13
6.已知向量的夹角为120°,且,则向量在向量方向上的投影为( ).
A. B. C. D.
7.某空间几何体的三视图如图所示,则该几何体的体积为( ).
A. B. C. D.
8.已知双曲线的左、右焦点分别为为坐标原点. 是双曲线在第一象限上的点,直线分别交双曲线左、右支于另一点.若,且,则双曲线的离心率为( ).
A. B. C. D.
9.已知命题,使;命题,下列真命题的( ).
A. B. C. D.
10.已知抛物线的焦点为,为抛物线上的两点,若为坐标原点,则的面积( ).
A. B. C. D.
11.为了得到,只需要将作如下变换( ).
A.向右平移个单位 B.向右平移个单位
C. 向左平移个单位 D.向右平移个单位
12.若实数满足,则的最小值为( ).
A. B.2 C. D.8
二、填空题(本大题共4小题,每小题5分,共20分,把答案填在答题纸的横线上.)
13.函数的单调递减区间是 .
14.在中,且,则角的大小为 .
15.已知直三棱柱(侧棱垂直于底面)的各顶点都在球的球面上,且,若三棱柱的体积等于,则球的体积为 .
16.设数列的前项和为,且为常数列,则 .
三、解答题(本大题共6个小题,第22、23题每题10分,其余各题每题12分,共70分.解答应写出文字说明,证明过程或演算步骤.)
17. 在锐角中,角的对边分别为,且.
(1)求角的大小;
(2)若函数的值域.
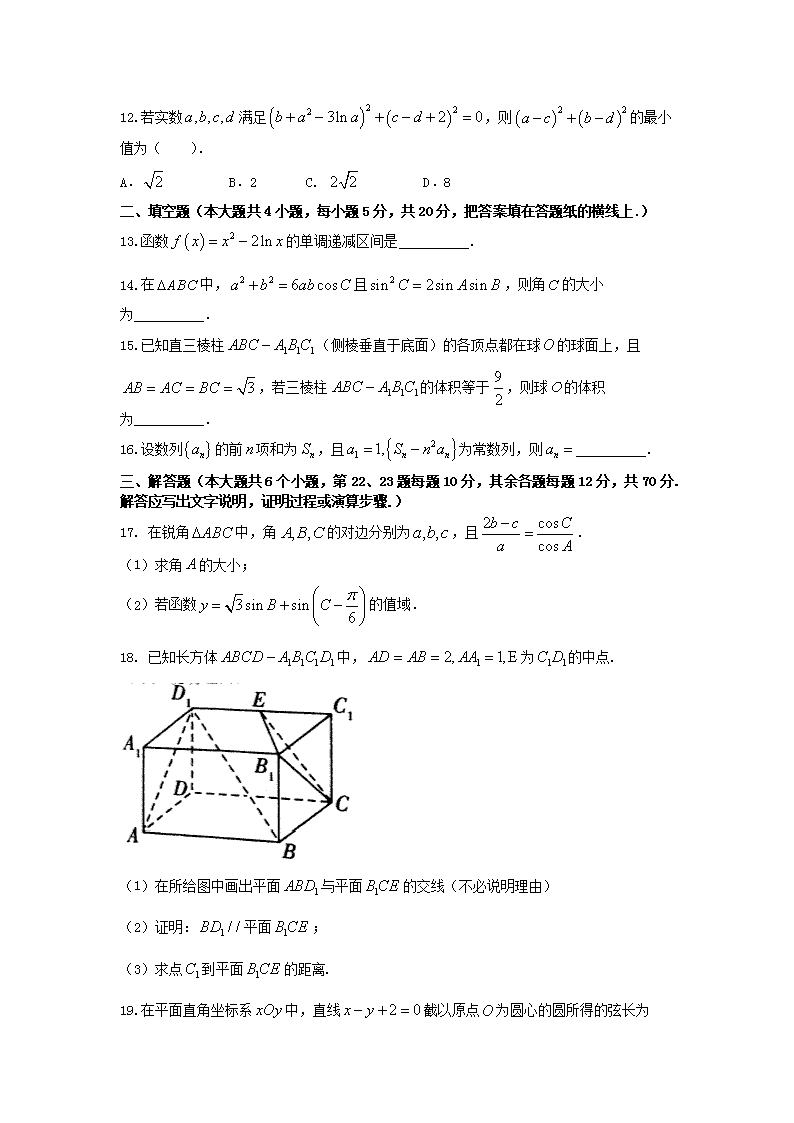
18. 已知长方体中,为的中点.
(1)在所给图中画出平面与平面的交线(不必说明理由)
(2)证明:平面;
(3)求点到平面的距离.
19.在平面直角坐标系中,直线截以原点为圆心的圆所得的弦长为
,
(1)求圆的方程;
(2)若直线与圆切于第一象限,且与坐标轴交于点,求的最小值及此时直线的方程.
20.如图,在平面直角坐标系中,已知椭圆的离心率为,经过椭圆的左顶点作斜率为的直线交椭圆于点,交轴点.
(1)求椭圆的方程;
(2)已知点为线段的中点,,并且交椭圆与点,求的最小值.
21.设函数.
(1)若,求函数的极值;
(2)若是函数的极值点,1和是函数的两个不同零点,且,求;
(3)若对任意,都存在,使得成立产,求实数的取值范围.
22.在平面直角坐标系中,以坐标原点为极点,轴正半轴为极轴建立坐标系,曲线
的参数方程为(为参数),曲线的极坐标方程为,
(1)求曲线的普通方程,曲线的直角坐标方程;
(2)曲线与相交于两点,点,求的值.
23.设函数.不等式的解集为.
(1)求;
(2)当时,证明:.
试卷答案
一、选择题
1-5: ACAAAA 6-10: DCBDC 11、12:CD
二、填空题
13. 14. 15. 16.
三、解答题
17.解:(1)∵,∴,
∴,
∴……………………8分
∵为锐角,∴;,∴…………………………10分
∴,∴函数的值域为……………………12分
18.(1)(2)略,(3)
19.(1);(2)最小值为4,的直线方程为.
20.(1);(2);
21.(1)当时,有极小值,无极大值;
(2)(3)略.
22.(1);
(2)
23.解:(1)原不等式等价于
或或,解得,∴…………………5分
(2)证明:当,即时,
要证:,即证,
∵,
∴………………………………………………10分