- 463.50 KB
- 2021-04-13 发布
宁夏长庆高级中学2018—2019学年第二学期高二期中
数学(理科)试卷
满分 150分 时间 120分钟
第I卷
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.复数 ( )
A. B. C. D.
2.下列求导正确的是 ( )
A. B.
C. D.
3.已知直线y=kx是曲线y=ln x的切线,则k的值是 ( )
A.e B.-e C. D.-
4.已知函数图象与轴恰有两个交点,则 ( )
A. -2或2 B. -9或3 C. -1或1 D. -3或1
5.函数,则的值为 ( )
A. B. C. D.8
6. 当用反证法证明命题:“设为实数,则方程至少有一个实根”时,要做的假设是: ( )
A.方程没有实根 B.方程至多有一个实根
C.方程至多有两个实根 D.方程恰好有两个实根
7.若函数在是增函数,则的取值范围为( )
A.[-1,0] B.[-1,+∞) C.[0,3] D.[3,+∞)
8. 若,,,则的大小关系为 ( )
A. B. C. D.
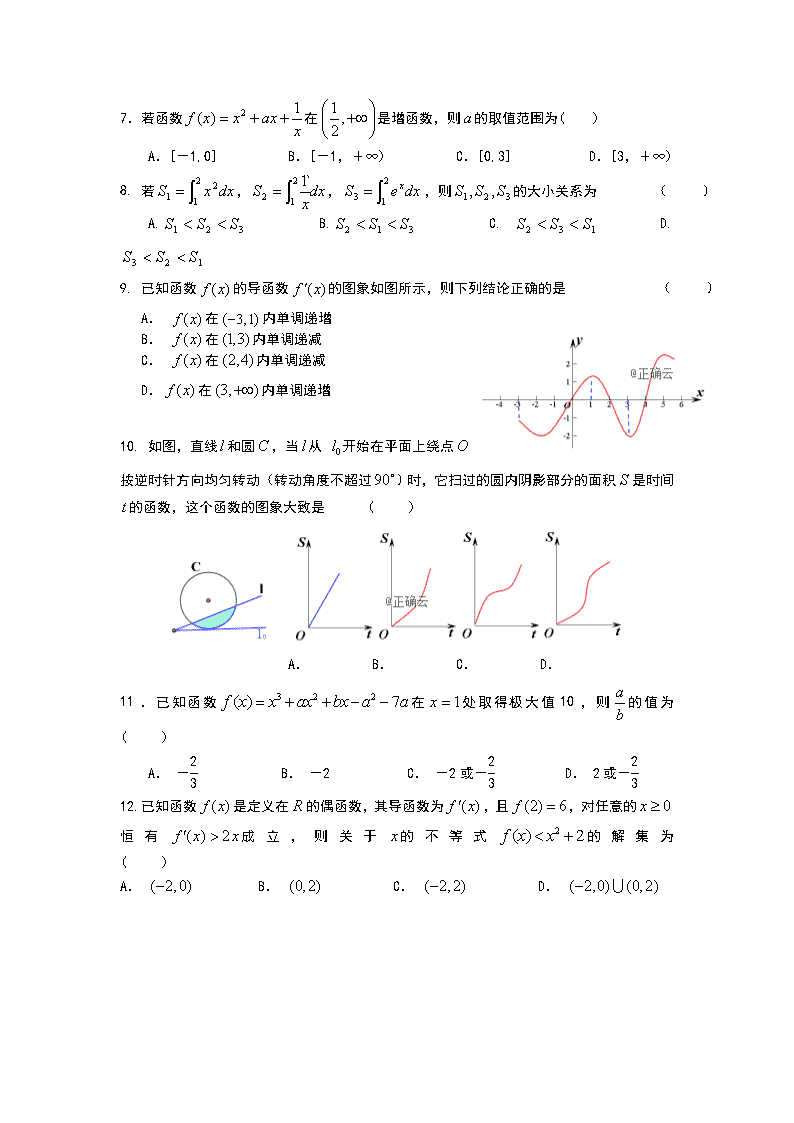
9. 已知函数的导函数的图象如图所示,则下列结论正确的是 ( )
A. 在内单调递增
B. 在内单调递减
C. 在内单调递减
D.在内单调递增
10. 如图,直线和圆,当从 开始在平面上绕点按逆时针方向均匀转动(转动角度不超过)时,它扫过的圆内阴影部分的面积是时间 的函数,这个函数的图象大致是 ( )
A. B. C. D.
11.已知函数在处取得极大值10,则的值为 ( )
A. - B. -2 C. -2或- D. 2或-
12.已知函数是定义在的偶函数,其导函数为,且,对任意的恒有成立,则关于的不等式的解集为 ( )
A. B. C. D.
第Ⅱ卷
二、填空题:本大题共4小题,每小题5分,共20分.
13.函数的递增区间是 __.
14.已知数列的第一项,且,则数列的通项公式为______________________.
15. 已知复数,则 __.
16. 已知函数是定义在上的奇函数,当时,,给出以下命题:
① 函数有个零点; ② 当时,;
③ 若关于的方程有解,则实数的取值范围是;
④ 对恒成立;
其中,正确命题的序号是__________.
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.
17.计算由直线,曲线所围成图形的面积
(本小题满分10分)
18.实数取什么值时,复数是,(1)实数;(2)纯虚数;(3)复平面内表示复数的点位于第四象限.
(本小题满分12分)
19.用总长为米的钢条制作一个长方体容器的框架,如果所制容器的底面的一条边比另一条边长米,那么高为多少时,容器的容积最大?并求它的最大容积。
(本小题满分12分)
20. 是不全相等的正实数,求证:
(本小题满分12分)
21.设函数 ,曲线在点处的切线方程为
(1)求的解析式;
(2)证明:曲线上任一点处的切线与直线和直线所围成的三角形面积为定值,并求此定值.
(本小题满分12分)
22. 已知函数
(1). 若在处取得极值,求的值;
(2). 求函数在 上的最大值.
(本小题满分12分)
答案
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1
2
3
4
5
6
7
8
9
10
11
12
C
B
C
A
B
A
D
B
C
D
A
D
二、填空题:本大题共4小题,每小题5分,共20分.
13. 14.
15. 16. (2),(4)
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.
17. 解:
解二:
18.解:(1)
(2)
(3)
19. 设底面一边长为米,另一边长为米,高为米
20. 证明:
21. 解:(1)函数 ,曲线在点处的切线方程为
(2)设曲线上任意一点为
曲线在点P处的切线方程为:
曲线上任一点处的切线与直线的交点为
曲线上任一点处的切线与直线交点为
22. (1)因为f(x)=lnx-ax2+(a-2)x,所以函数的定义域为(0,+∞).
所以f′(x) =-2ax+(a-2)==.
因为f(x)在x=1处取得极值,即f′(1) =-(2-1)(a+1)=0,解得a=-1.
当a=-1时,在(,1)上f′(x)<0,在(1,+∞)上f′(x) >0,
此时x=1是函数f(x)的极小值点,所以a=-1.
(2)因为a20,所以f(x)在(0,)上单调递增,在(,+∞)上单调递减.
①当0