- 1.11 MB
- 2021-04-13 发布
高三物理考试
一、选择题
1.甲、乙两汽车同向匀速行驶,乙在前,甲在后.某时刻两车司机听到警笛提示,同时开始
刹车,结果两车刚好没有发生碰撞,如图为两车刹车后匀减速运动的 v-t 图象.以下分析
正确的是( )
A. 甲车刹车的加速度的大小为 0.5 m/s2
B. 两车开始刹车时的距离为 100 m
C. 两车刹车后间距一直在减小
D. 两车都停下来后相距 25 m
【答案】B
【解析】
【详解】AB.由题图可知,两车速度相等时,经历的时间为 20 s,甲车的加速度
乙车的加速度
此时甲车的位移
乙车的位移
两车刚好没有发生碰撞,则开始刹车时两车的距离
,
故 A 错误,B 正确;
C.两车刹车后甲的速度先大于乙的速度,两者距离减小,后甲的速度小于乙的速度,两者距
2 2
1
25 m / s 1m / s25a
−= = −
2 2
2
15 m / s 0.5m / s30a = − = −
2
1
1 125 20m 1 400m 300m2 2x v t a t= + = × − × × =甲 甲
2
2
1 115 20m 0.5 400m 200m2 2x v t a t= + = × − × × =乙 乙
300 m 200 m 100 mx∆ = - =
离增大,故 C 错误;
D.20 s 时,甲、乙的速度都为
,
根据图象与坐标轴围成的面积表示位移可知,两车都停下来后相距
故 D 错误.
2.如图所示,倾角 θ=37°的上表面光滑的斜面体放在水平地面上.一个可以看成质点的小球
用细线拉住与斜面一起保持静止状态,细线与斜面间的夹角也为 37°.若将拉力换为大小不变、
方向水平向左的推力,斜面体仍然保持静止状态.sin37°=0.6,cos37°=0.8.则下列说法正确
的是( )
A. 小球将向上加速运动
B. 小球对斜面的压力变大
C. 地面受到的压力不变
D. 地面受到的摩擦力不变
【答案】B
【解析】
AB、小球处于静止状态,所以合外力为零,小球受力为:竖直向下的重力 G、斜面对小球
的 支 持 力 和 细 线 对 小 球 的 拉 力 , 把 三 个 力 正 交 分 解 , 由 平 衡 方 程 为 :
, , 两 式 联 立 解 得 : ,
;将拉力换为大小不变、方向水平向左的推力,小球受力为:竖直向下的重力
G、斜面对小球的支持力 和方向水平向左的推力,把三个力正交分解,沿斜面方向有
, 故 小 球 处 于 静 止 状 态 , 垂 直 斜 面 方 向
,小球对斜面的压力变大,故 A 错误,B 正确;
CD、斜面体与小球为整体,受力为:竖直向下的重力 、地面对斜面体的支持力 、地
1 25 m/s 20 m/s 5 m/sv v a t甲= + = - =
1 30 25 5 m 12.5 m2 ( )x∆ ′ × ×= - =
NF F
cos37 sin37NG F F° = + ° cos37 sin37F G° = ° 3 G4F =
7
20NF G=
NF ′
cos37 sin37F G° = °
5cos37 sin37 4NF G F G′ = °+ ° =
G′ NF ′′
面对其的摩擦力和细线对小球的拉力 ;将拉力换为大小不变、方向水平向左的推力,受力
为:竖直向下的重力 、地面对斜面体的支持力 、地面对其的摩擦力和方向水平向左
的推力 ,所以地面对斜面体的支持力变小,地面对其的摩擦力变大,故 CD 错误;
故选 B。
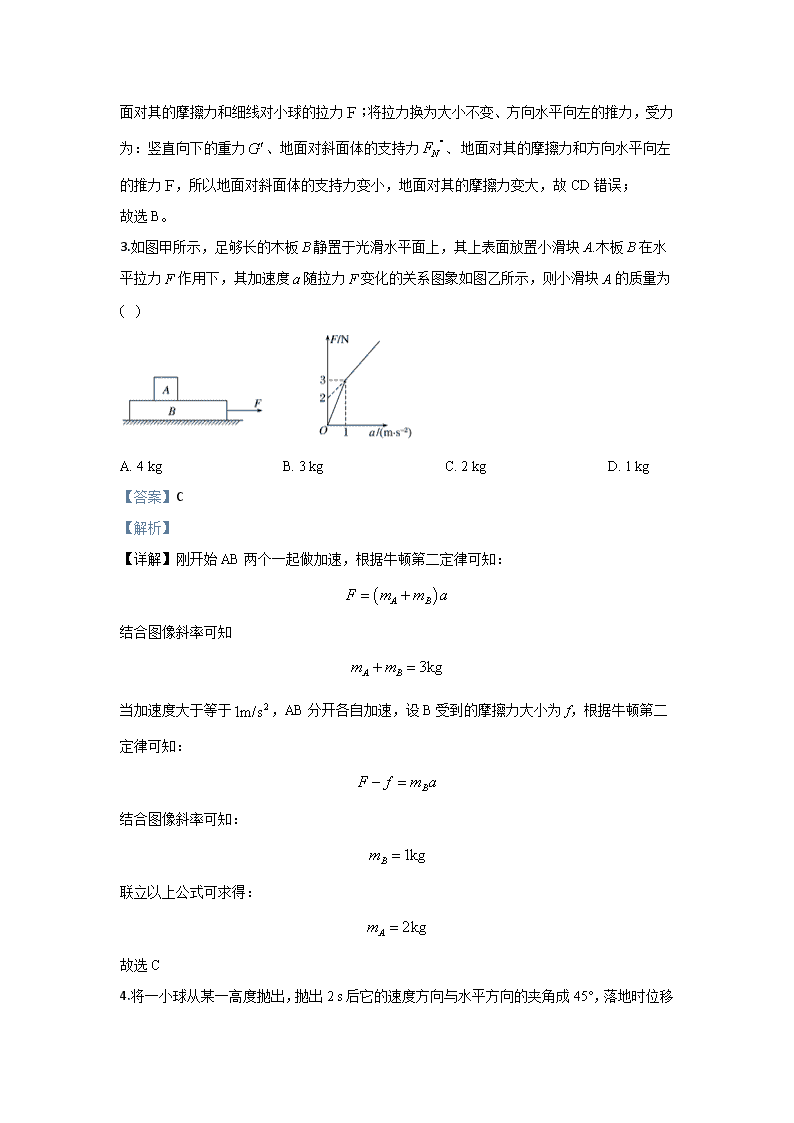
3.如图甲所示,足够长的木板 B 静置于光滑水平面上,其上表面放置小滑块 A.木板 B 在水
平拉力 F 作用下,其加速度 a 随拉力 F 变化的关系图象如图乙所示,则小滑块 A 的质量为
( )
A. 4 kg B. 3 kg C. 2 kg D. 1 kg
【答案】C
【解析】
【详解】刚开始 AB 两个一起做加速,根据牛顿第二定律可知:
结合图像斜率可知
当加速度大于等于 ,AB 分开各自加速,设 B 受到的摩擦力大小为 f,根据牛顿第二
定律可知:
结合图像斜率可知:
联立以上公式可求得:
故选 C
4.将一小球从某一高度抛出,抛出 2 s 后它的速度方向与水平方向的夹角成 45°,落地时位移
F
G′ NF ′′′
F
( )A BF m m a= +
3kgA Bm m+ =
21m/s
BF f m a− =
1kgBm =
2kgAm =
与水平方向成 60°,不计空气阻力,重力加速度 g=10 m/s2,则下列说法正确的是
A. 小球做平抛运动的初速度是 10m/s
B. 抛出点距地面的高度是 60m
C. 小球做平抛运动的初速度是 m/s
D. 抛出点距地面的高度是 240m
【答案】D
【解析】
由平抛运动的规律有:抛出 1s 后, ,得 ;落地时
得 : , 抛 出 点 距 地 面 的 高 度
.故 D 正确,ABC 错误.故选 D.
5.如图所示,滑块以初速度 滑上表面粗糙的固定斜面,到达最高点后又返回到出发点。
则下列能大致描述滑块整个运动过程中的速度 v、加速度 a、动能 、重力对滑块所做的功
W 与时间 t 或位移 x 之间关系的图象是 取初速度方向为正方向
A.
20 2
tan 45 y
x
v
v
° = 0 1 20m/syv v gt= = =
2
0
tan 60 2
gty
x v
° = = 0
2
2 tan 60 4 3svt g
°= =
2
2
1 240m2h gt= =
0v
kE
( )( )
B
C.
D.
【答案】D
【解析】
物体上滑时的加速度大小 a1= =gsinθ+μgcosθ,方向沿斜面向下.下滑
时的加速度大小 a2= =gsinθ-μgcosθ,方向沿斜面向下,则知 a1>a2,方
向相同,均为负方向.因 v-t 线的斜率等于加速度,可知选项 AB 错误;动能是标量,不存
在负值.故 C 错误.重力做功 W=-mgh=-mgxsinθ,故 D 正确.故选 D.
点睛:解决本题的关键根据牛顿第二定律得出上滑和下滑的加速度,判断出物体的运动情
况.要通过列方程分析图象的物理意义.
6.如图所示,真空中有一匀强电场(图中未画出),电场方向与圆周在同一平面内,△ABC
是圆的内接直角三角形,∠ACB=26.5°,O 为圆心,半径 R=5cm。位于 A 处的粒子源向平
面内各个方向发射初动能均为 8eV、电荷量+e 的粒子,有些粒子会经过圆周上不同的点,
其中到达 B 点的粒子动能为 12eV,达到 C 点的粒子电势能为-4eV(取 O 点电势为零)。忽
略粒子的重力和粒子间的相互作用,sin53°=0.8。下列说法正确的是
mgsin mgcos
m
θ µ θ+
mgsin mgcos
m
θ µ θ−
A. 匀强电场的场强大小为 100V/m
B. 圆周上 B、C 两点的电势差为-4V
C. 圆周上 A、C 两点的电势差为 12V
D. 当某个粒子经过圆周上某一位置时,可以具有 6eV 的电势能,且同时具有 6eV 的动能
【答案】A
【解析】
【详解】根据电势的定义可以求出 C 点的电势
根据匀强电场 特征可知:
UAO=UOC=4V
解得:
。
根据动能定理
,
解得:
。
由于 B 点的电势等于 O 点的电势等于 0,所以 O 与 B 是等势点,连接 OB,则 OB 为匀强电
场的等势面,过 A 点做 OB 的垂线交 OB 与 D 点,则 AD 的方向就是该电场的场强方向,如
图:
的
4VC
C
E
e
ϕ = −
4VA
ϕ =
4eVAB KB KAW E E= − =
0VB
ϕ =
根据几何关系可知
∠AOB=53°,AD=0.04m。
由于 OBD 是等势面,所以
。
故 A 正确;
B. 圆周上 B、C 两点的电势差为
故 B 错误;
C. 圆周上 A、C 两点的电势差为
故 C 错误;
D. 该圆周上电势最高的点到比 O 点高:
,
所以最大电势能只能是 5eV。故 D 错误。
7.如图所示,固定的倾斜粗糙细杆与水平地面间的夹角为 θ=37°,质量为 1 kg 的圆环套
在细杆上.轻质弹簧的一端固定在水平地面上的 O 点,另一端与圆环相连接,当圆环在 A
点时弹簧恰好处于原长状态且与轻杆垂直.将圆环从 A 点由静止释放,滑到细杆的底端 C
点时速度为零.若圆环在 C 点获得沿细杆向上且大小等于 2 m/s 的初速度,则圆环刚好能再
次回到出发点 A.已知 B 为 AC 的中点,弹簧原长为 0.3 m,在圆环运动过程中弹簧始终在弹
性限度内,重力加速度 g=10 m/s2,sin 37°=0.6,cos 37°=0.8.
A. 下滑过程中,圆环受到的合力一直在增大
B. 下滑过程中,圆环与细杆摩擦产生的热量为 2 J
C. 在圆环从 C 点回到 A 点的过程中,弹簧对圆环做的功为 1.2 J
D. 圆环下滑经过 B 点的速度一定小于上滑时经过 B 点的速度
【答案】D
100V/mUE d
==
( )0 4 4VBC B CU ϕ ϕ= − = − − =
( )4 4 8VAC A CU ϕ ϕ= − = − − =
2
max 5 10 100 5R E Vϕ −= ⋅ = × × =
【解析】
【详解】A.下滑过程中,圆环受到重力、摩擦力、弹簧的弹力和杆的支持力,弹簧的弹力逐
渐增大,圆环滑到细杆底端时速度为零,可知合力先减小后增大,故 A 错误.
B.设下滑过程中,圆环与细杆摩擦产生的热量为 Q,上滑时产生的热量也为 Q.由能量守恒
定律得:下滑过程有
Q+Ep=mgh
上滑过程有
mv02+Ep=Q+mgh
解得
Q= mv02= ×1×22 J=1 J,
故 B 错误;
C.根据上面公式可计算得:
Ep=mgh-Q=1×10×0.3×0.8 J-1 J=1.4 J,
故 C 错误.
D.从 B 到 C,由动能定理得:
从 C 到 B,由动能定理得:
对比可得 vB1<vB2,即圆环下滑经过 B 点的速度一定小于上滑时经过 B 点的速度,故 D 正
确.
8.如图所示,均匀带电的半圆环在圆心 O 点产生的电场强度为 E、电势为 ,把半圆环分成
AB、BC、CD 三部分。下列说法正确的是
1
2
1
4
1
4
2
1
1 1 02 2F f BW W mgh mv- - + = -
2
2
1 102 2F f BW W mgh mv- - = -
ϕ
A. BC 部分在 O 点产生的电场强度的大小为
B. BC 部分在 O 点产生的电场强度的大小为
C. BC 部分在 O 点产生的电势为
D. BC 部分在 O 点产生的电势为
【答案】AD
【解析】
如图所示,B、C 两点把半圆环等分为三段。
设每段在 O 点产生的电场强度大小均为 E′。AB 段和 CD 段在 O 处产生的场强夹角为 120°,
它们的合场强大小为 E′则 O 点的合场强:E=2E′,则:E′=E/2;故圆弧 BC 在圆心 O 处产生
的场强为 E/2。电势是标量,设圆弧 BC 在圆心 O 点产生的电势为 φ′,则有 3φ′=φ,则
φ′=φ/3,故选 AD。
点睛:本题要注意电场强度是矢量,应根据平行四边形定则进行合成,掌握电场的叠加原理;
电势是标量,可直接取代数和.
9.如图所示,小球 A、B、C 的质量分别为 m、m、2m,A 与 BC 间通过铰链用轻杆连接,杆长
为 L,B、C 置于水平地面上。现让两轻杆并拢,将 A 由静止释放下降到最低点的过程中,A、
B、C 在同一竖直平面内运动,忽略一切摩擦,重力加速度为 g。则
A. A、B、C 组成的系统水平方向动量守恒
B. A、C 之间的轻杆始终对 C 做正功
2
E
3
E
2
ϕ
3
ϕ
C. A 与桌面接触时具有水平方向的速度
D. A 与桌面接触时的速度大小为
【答案】AD
【解析】
A、B、C 组成的系统水平方向受到的合力为零,则水平方向动量守恒,选项 A 正确;小球 C
的速度先增大后减小,则 A、C 之间的轻杆对 C 先做正功后做负功,选项 B 错误;系统初
动量为零,水平方向末动量也为零,因 A 与桌面接触时,三个球的水平速度相等,则根据
水平方向动量守恒可知三个球的水平方的速度均为零,选项 C 错误;竖直方向,当 A 与桌
面接触时,小球 A 的重力势能转化为系统的动能,因 BC 的速度为零,则 mgL= mv2,解
得 ,选项 D 正确;故选 AD.
10.研究表明,地球自转周期在逐渐改变,3 亿年前地球自转的周期约为 22 小时.假设这种
趋势会持续下去,且地球的质量、半径都不变,则经过若干亿年后
A. 近地卫星的向心加速度比现在大
B. 近地卫星的运行的周期与现在相等
C. 同步卫星的向心加速度比现在小
D. 同步卫星的运行速度比现在大
【答案】BC
【解析】
近地卫星由万有引力提供圆周运动向心力,据 知,近地卫星的运行加速度
,地球的质量和半径都不变,故运行加速度大小不变,所以 A 错误;根据
可得 ,则近地卫星的运行的周期与现在相等,选项 B 正确;
万有引力提供圆周运动向心力有 ,周期 ,由于地球
自转周期变慢,故同步卫星的轨道高度 r 变大,据向心加速度 知,向心加速度减小,
故 C 正确.又据 知,轨道半径 r 变大,卫星的线速度变小,所以 D 错误.故选
2gl
1
2
2v gL=
2
mMG maR
=
2
GMa R
=
2
2 2
4mMG mR RT
π=
3
2 RT GM
π=
2 2
2 2
4mM vG m m rr r T
π==
2 34 rT GM
π=
2
GMa r
=
GMv r
=
BC.
11.如图所示,在倾角 θ=30°的光滑斜面上有两个用轻质弹簧相连接的物块 A、B,它们的
质量均为 m,弹簧的劲度系数为 k,C 为一垂直斜面的固定挡板.系统处于静止状态,现开
始用一沿斜面方向的力 F 拉物块 A 使之以加速度 a 向上做匀加速运动,物块 B 刚要离开 C
时力 F 的大小恰为 2mg.则( )
A. 物块 B 刚要离开 C 时受到的弹簧弹力为
B. 加速度
C. 这个过程持续的时间为
D. 这个过程 A 的位移为
【答案】ACD
【解析】
【详解】A.物块 B 刚要离开 C 时 B 对 C 的弹力恰好为零,对 B,由平衡条件得,此时弹簧
的弹力:
故 A 正确;
B.B 刚要离开 C 时,对 A,由牛顿第二定律得:
解得
a=g,
故 B 错误;
D.刚开始时,对 A 由平衡条件得:
,
B 刚要离开 C 时,弹簧弹力:
2
mg
1
2a g=
2m
k
mg
k
sin = 2
mgF mg θ=弹
F mgsin F maθ 弹- - =
1kx mgsinθ=
,
整个过程 A 的位移:
x=x1+x2,
解得:
,
故 D 正确;
C.物块 A 做初速度为零的匀加速直线运动,
,
解得运动时间
,
故 C 正确.
12.如图所示,在真空中,半径为 R 圆形区域内存在垂直于纸面向外的匀强磁场,磁感应
强度为 B,AB 为其竖直直径。一束质子在纸面内以相同的速度射向磁场区域,质子的电量
为 m。在这束质子中有两个分别从距水平直径为 的 a 点和 的 b 点入射,沿着半径
入射的质子恰好到达 B 点,在 B 点装置一与水平直径平行的弹性挡板,质子与挡板发生碰
撞时无能量损失。则以下说法正确的是( )
A. 这束质子的速率为
B. 质子到达 B 点后沿原路返回
C. 所有质子将从磁场右侧平行射出
的
2F kx弹=
mgx k
=
21
2x at=
2mt k
=
3
2 R 1
2 R
eBR
m
D. 从 a 点入射的质子在磁场中运动的时间与从 b 点入射的质子在磁场中运动的时间的比值
为
【答案】ACD
【解析】
【详解】A.沿着半径入射的质子恰好到达 B 点,其轨迹半径为 ,由洛仑兹力提供向
心力得:
解得
故 A 正确;
BC.如图所示:
假设从任意点 E 水平射入的质子,其做匀速圆周运动的圆心为 D,连接两交点及两圆心.由
于 DE∥OC,且 DE=OC,则四边形 DEOC 是平行四边形,所以 DC=OE=R,所以从任意点
E 水平入射的质子都能到达 B 点,此为磁聚焦模型;所有质子到 B 点后与弹性挡板碰撞,
速度大小不变,方向关于直径 AB 对称,将从磁场右侧沿着水平方向射出,此为磁发散模型,
故 B 错误、C 正确;
D.从 a 点入射的质子到达 B 的过程中在磁场中运动的圆心角为 ,从 b 点入射的质子到
达 B 的过程中在磁场中运动的圆心角为 ,根据对称性,可得二者在磁场中运动的时间
之比为 ,故 D 正确。
13.利用图甲所示的装置验证动量守恒定律。在图甲中,气垫导轨上有 A、B 两个滑块,滑
块 A 右侧带有一弹簧片,左侧与打点计时器(图中未画出)的纸带相连;滑块 B 左侧也带
有一弹簧片,上面固定一遮光片,光电计时器(未完全画出)可以记录遮光片通过光电门的
5: 2
r R=
2vBev m r
=
eBRv m
=
150°
60°
5: 2
时间。
实验测得滑块 A 质量 m1=0.3kg,滑块 B 的质量 m2=0.1kg,遮光片的宽度 d 用游标卡尺测
量,如图丙所示;打点计时器所用的交流电的频率f=50Hz。将光电门固定在滑块 B 的右侧,
启动打点计时器,给滑块 A 一向右的初速度,使它与 B 相碰;碰后光电计时器显示的时间∆tB
=2.86×10-3s,碰撞前后打出的纸带如图乙所示。
(1)遮光片的宽度 d=____cm。
(2)计算可知两滑块相互作用以前系统的总动量为_____kg⋅m/s,两滑块相互作用以后系统
的总动量为_____kg⋅m/s。(计算结果保留两位小数)
(3)若实验相对误差绝对值 即可认为系统
动量守恒,则本实验在误差范围内_____验证动量守恒定律。(填“能”或“不能”)
(4)两滑块作用前后总动量不完全相等的主要原因是____________________。
【答案】 (1). (1)0.830cm (2). (2)0.60kg⋅m/s, (3). 0.58kg⋅m/s (4). (3)
能 (5). (4)纸带与打点计时器限位孔有摩擦
【解析】
(1)遮光片的宽度 d=0.8cm+0.05mm×6=0.830cm;
(2)打点计时器的打点时间间隔为:t=0.02s.
由图(b)所示纸带可知,碰撞前 A 的速度: ,碰撞后 A
0 0100 50 0r
碰撞前后总动量之差
碰撞前总动量
σ = × ≤
0.0400 / 2 /0.02
A
A
xv m s m st
= = =
的速度为: ,碰撞后 B 的速度:
,
碰撞前后系统总动量分别为:p=m1vA=0.3×2.0=0.60kg•m/s,
p′=m1vA′+m2vB′=0.30×0.97+0.10×2.86≈0.58kg•m/s,
(3)相对误差:
由此可知,在误差范围内验证了动量守恒定律.
(4)两滑块作用前后总动量不完全相等的主要原因是纸带与打点计时器限位孔有摩擦.
点睛:本题考查了验证动量守恒定律实验,由纸带求出滑块速度及根据光电门求出速度是正
确解题的关键、应用动量计算公式即可明确碰撞前后的动量,则可验证动量守恒.
14.某研究小组收集了两个电学元件:电阻 R0(约为 2 kΩ)和手机中的锂电池(电动势 E 标称值
为 3.7 V,允许最大放电电流为 100 mA).实验室备有如下器材:
A.电压表 V(量程 3 V,电阻 RV 约为 4.0 kΩ)
B.电流表 A1(量程 100 mA,电阻 RA1 约为 5 Ω)
C.电流表 A2(量程 2 mA,电阻 RA2 约为 50 Ω)
D.滑动变阻器 R1(0~40 Ω,额定电流 1 A)
E.电阻箱 R2(0~999.9 Ω)
F.开关 S 一只,导线若干
(1)为了测定电阻 R0 的阻值,小明设计了一电路,如图甲所示为其对应的实物图,图中的电
流表 A 应选______(选填“A1”或“A2”),请将实物连线补充完整_______.
(2)为测量锂电池的电动势 E 和内阻 r,小红设计了如图乙所示的电路图.根据测量数据作出
图象,如图丙所示.若该图线的斜率为 k,纵轴截距为 b,则该锂电池的电动势 E=
____,内阻 r=_____(用 k、b 和 R2 表示).该实验的测量值偏小,造成此系统误差的主要原
0.0194 / 0.97 /0.02Av m s m s′ = =
3
0.0100 / 2.86 /3.5 10B
B
dv m s m st −′ = ≈×
=
0.60 0.58100% 100% 3.3% 5%0.60
p p
p
− ′ −× = × ≈ <
2
1 1
U R
−
因是__________.
【答案】(1)A2;见解析图;(2) ; ;电压表分流
【解析】
试 题 分 析 : ( 1 ) 电 压 表 量 程 是 3V , 通 过 待 测 电 阻 的 最 大 电 流
,
因此电流表应选电流表 A2(量程 2mA,电阻 RA2 约为 50Ω);待测电阻 R0 阻值约为 2kΩ,滑
动变阻器 R1(0~40Ω,额定电流 1A)与电阻箱 R2(0~999.9Ω)最大阻值均小于待测电阻
阻值,变阻器采用限流接法时待测电阻电压与电流变化范围较小,不能测多组实验数据,为
测多组实验数据,减小实验误差,滑动变阻器应采用分压接法; ,
, ,电流表应该采用内接法,实物电路图如图所示.
(2)由图乙所示电路可知, ,则 ,因此图象的纵轴截
距 ,电动势 ,图象的斜率 ,则电源内阻 。
考点:测量电源的电动势及内阻
【名师点睛】此题考查了测量电源的电动势及内阻的实验;根据待测电阻与滑动变阻器阻值
间的关系确定滑动变阻器的接法,根据待测电阻阻值与电表内阻间的关系确定电流表的接法
是正确连接实物电路图的前提与关键。
15.如图所示,一长度 LAB=4.98m,倾角 θ=30°的光滑斜面 AB 和一固定粗糙水平台 BC 平
滑连接,水平台长度 LBC=0.4m,离地面高度 H=1.4m,在 C 处有一挡板,小物块与挡板
碰撞后原速率反弹,下方有一半球体与水平台相切,整个轨道处于竖直平面内。在斜面顶端
A 处静止释放质量为 m="2kg" 的小物块(可视为质点),忽略空气阻力,小物块与 BC 间的
动摩擦因素 μ=0.1,g 取 10m/s2。问:
(1)小物块第一次与挡板碰撞前的速度大小;
(2)小物块经过 B 点多少次停下来,在 BC 上运动 总路程为多少;
(3)某一次小物块与挡板碰撞反弹后拿走挡板,最后小物块落在 D 点,已知半球体半径
r=0.75m,OD 与水平面夹角为 α=53°,求小物块与挡板第几次碰撞后拿走挡板?(取
)
【答案】(1)7 m/s;(2)63 次 24.9m(3)25 次
【解析】
试题分析:小物块从开始运动到与挡板碰撞,重力、摩擦力做功,运用动能定理。求小物块
经过 B 点多少次停下来,需要根据功能转化或动能定理求出小物块运动的路程,计算出经
过 B 点多少次。小物块经过平抛运动到达 D 点,可以求出平抛时的初速度,进而求出在 BC
段上运动的距离以及和当班碰撞的次数。
(1)从 A 到 C 段运用动能定理
mgsin - LAB= mv2
v=7m/s
(2)从开始到最后停下在 BC 段所经过的路程为 x
mgsin LAB- mgx=0
x=24.9m
=31.1
经过 AB 的次数为 31 2+1=63 次
(3)设小物块平抛时的初速度为 V0
的
H -r = gt2
r+ =v0t
v0=3 m/s
设第 n 次后取走挡板
mv2- mv02=2 Lbcn
n=25 次
考点:动能定理、平抛运动
【名师点睛】解决本题的关键一是要会根据平抛运动的规律求出落到 D 时平抛运动的初速
度;再一个容易出现错误的是在 BC 段运动的路程与经过 B 点次数的关系,需要认真确定。
根据功能关系求出在 BC 段运动的路程。
16.如图,在 区域内存在与 xy 平面垂直的匀强磁场,磁感应强度的大小为 B.在
t=0 时刻,一位于坐标原点的粒子源在 xy 平面内发射出大量同种带电粒子,所有粒子的初
速度大小相同,方向与 y 轴正方向的夹角分布在 0~180°范围内。已知沿 y 轴正方向发射的
粒子在 时刻刚好从磁场边界上 点离开磁场。求:
⑴ 粒子在磁场中做圆周运动的半径 R 及粒子的比荷 q/m;
⑵ 此时刻仍在磁场中的粒子的初速度方向与 y 轴正方向夹角的取值范围;
⑶ 从粒子发射到全部粒子离开磁场所用的时间。
【答案】⑴
0 3x a≤ ≤
0t t= ( )3 ,P a a
⑵速度与 y 轴的正方向的夹角范围是 60°到 120°
⑶从粒子发射到全部离开所用时间为
【解析】
试题分析:(1)沿 y 轴正方向发射的粒子在磁场中的运动轨迹如图甲中的弧 所示,其圆心
为 C.由题给条件可以得出
①
此粒子飞出磁场所用的时间为
②
式中 T 为粒子做圆周运动的周期.
设粒子运动速度的大小为 v,半径为 R,由几何关系可得
③
由洛伦兹力公式和牛顿第二定律有
④
⑤
联立②③④⑤式,得
oP
2
3OCP
π∠ =
0 3
Tt =
2
3
R a=
2vqvB m R
=
2 RT v
π=
(2)依题意,同一时刻仍在磁场内的粒子到 O 点距离相同.在 时刻仍在磁场中的粒子应位
于以 O 点为圆心、OP 为半径的弧 上,如图甲所示.
乙
设此时位于 P、M、N 三点的粒子的初速度分别为 由对称性可知 与 OP、
与 OM、 与 ON 的夹角均为 π/3.设 与 y 轴正向的夹角分别为 ,由几何关
系有
对于所有此时仍在磁场中的粒子,其初速度与 y 轴正方向所成的夹角 θ 应满足
(3)在磁场中飞行时间最长的粒子的运动轨迹应与磁场右边界相切,其轨迹如图乙所示.由
几何关系可知,
由对称性可知,
从粒子发射到全部粒子飞出磁场所用的时间
考点:带电粒子在匀强磁场中的运动;牛顿第二定律;
点评:本题考查带电粒子在磁场中的运动,解题的关键在于确定圆心和半径,并能根据几何
关系确定可能的运动轨迹.
【此处有视频,请去附件查看】
17.如图,O、A、B 为同一竖直平面内的三个点,三点连线组成等腰直角三角形△OAB。将
0
2
3
q
m Bt
π=
0t
MN
.P M Nv v v、 、 Pv Mv
Nv M Nv v、 M N、θ θ
2
3 3M N
π πθ θ= , =
2
3 3
π πθ≤ ≤
OM OP= ME OP=
m 02 .t t=
一质量为 m 的小球以一定的初动能自 O 点水平向右抛出,小球在运动过程中通过 A 点。使
此小球带负电,电荷量为-q,同时加一匀强电场,场强方向与△OAB 所在平面平行。现从 O
点以同样的初动能沿某一方向抛出此带电小球,该小球通过了 A 点,到达 A 点时的动能是
初动能的 倍,若该小球从 O 点以同样的初动能沿另一方向抛出,通过 B 点,且到
达 B 点时的动能为初动能的 9 倍,重力加速度大小为 g,求:
(1)无电场时,小球到达 A 点时的动能与初动能的比值;
(2)电场强度 大小和方向。
【答案】(1) (2) ,方向与竖直方向成 75°。
【解析】
【详解】(1)小球做平抛运动,设初速度 v0。初动能 EK0,从 O 到 AB 的运动时间为 t,令 O
到 A 的竖直距离为 d。
水平方向
竖直方向
解得
根据动能定理可知小球到达 A 时的动能为
EKA ,
的
(5 4 3)+
0
5kA
k
E
E
= 6mgE q
=
0v t d=
21
2y gt d= =
0 4k
mgdE =
5
4
mgd=
所以
(2)加电场后,从 O 点到 A 点下降了 d,从 O 点到 B 点上升了 d,由能量守恒,电势能减
少了
在匀强电场中,沿着任意直线,电势的降落是均匀的,如图所示:
设直线 OB 上的 M 点的电势与 A 的电势相同,M 点到 O 点的距离是 x,如图,则有
解得
。
MA 是等势线,电场线与 MA 的垂线 OC 平行,∠OAM=30°,
设电场强度的大小是 E,则:
解得
,
方向与竖直方向成 75°。
0
5kA
k
E
E
=
5 4 3 3pA ko koE E E mgd mgd∆ = + − − =( )
09 3pB k koE E E mgd mgd∆ = − + =
3 tan32
pA
pB
Ex OAMEd
∆= = = ∠∆
6
3
dx =
12 2 pAqE d E= ∆
6mgE q
=