- 342.50 KB
- 2021-04-13 发布
绝密★启用前
2016-2017学年度武威五中质量检测
高二文科数学试卷
注意事项:
1. 答题前填写好自己的姓名、班级、考号等信息
2. 请将答案正确填写在答题卡上
一、 选择题(每小题5分)
1. 登山族为了了解某山高 y (km)与气温 x (°C)之间的关系,随机统计了4次山高与相应的气温,并制作了对照表:
气温 x (°C)
18
13
10
-1
山高 y (km)
24
34
38
64
由表中数据,得到线性回归方程 ,由此请估计出山高为72(km)处气温的度数为( )
A.-10 B.-8 C.-6 D.-6
2. 下列关于回归分析与独立性检验的说法正确的是( )
A.回归分析和独立性检验没有什么区别
B.回归分析是对两个变量准确关系的分析,而独立性检验是分析两个变量之间的不确定关系
C.回归分析研究两个变量之间的相关关系,独立性检验是对两个变量是否具有某种关系的一种检验
D.独立性检验可以100%确定两个变量之间是否具有某种关系
3. 在数列 中, , ,则 等于( )
A.
B.
C.
D.
4. 设 P 是△ ABC 所在平面内的一点, ,则( )
A. B.
C. D.
5. 设 是虚数单位,若复数 是纯虚数,则 的值为 ( )
A.-3
B.-1
C.1
D.3
6. 若 为虚数单位,复数 在复平面上对应的点位于( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
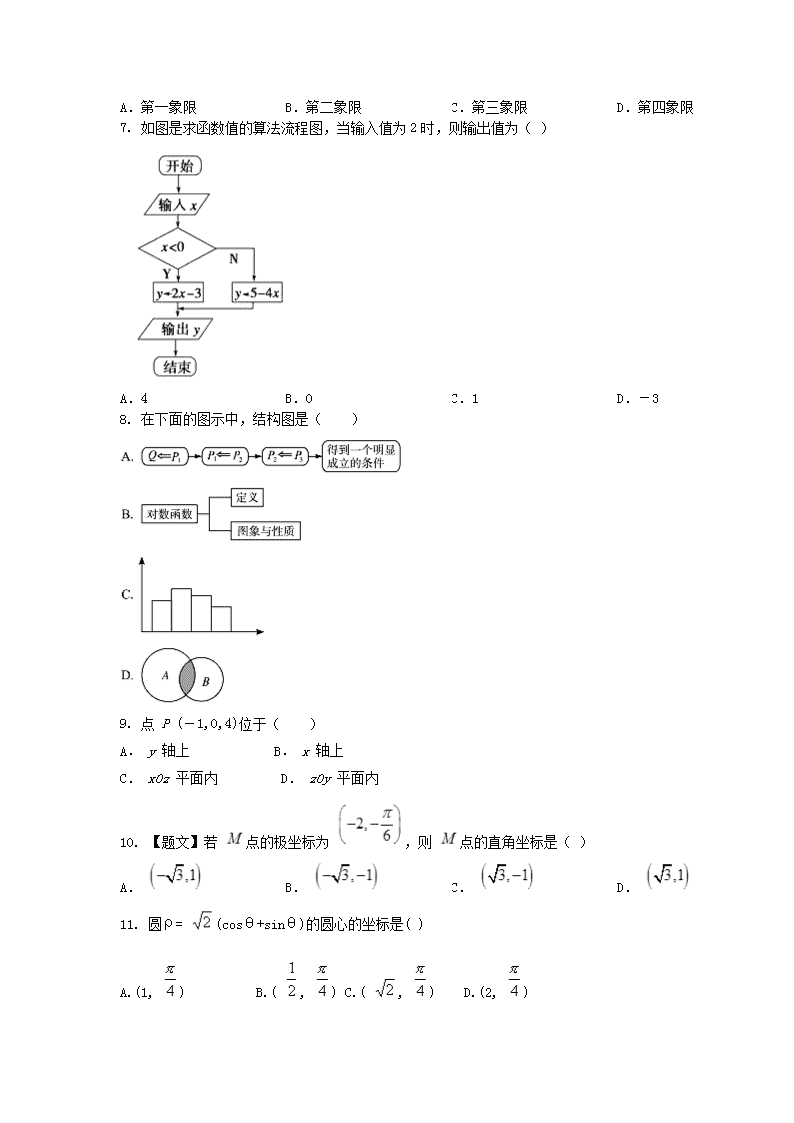
7. 如图是求函数值的算法流程图,当输入值为2时,则输出值为( )
A.4
B.0
C.1
D.-3
8. 在下面的图示中,结构图是( )
9. 点 P (-1,0,4)位于( )
A. y 轴上 B. x 轴上
C. xOz 平面内 D. zOy 平面内
10. 【题文】若 点的极坐标为 ,则 点的直角坐标是( )
A.
B.
C.
D.
11. 圆ρ= (cosθ+sinθ)的圆心的坐标是( )
A.(1, ) B.( , ) C.( , ) D.(2, )
12. 【题文】如图,O是半径为1的球的球心,点A、B、C在球面上,OA、OB、OC两两垂直,E、F分别为大圆弧AB与AC的中点,则E、F的球面距离是_____
二、 填空题(每小题5分)
13. 【题文】直线 ( 为参数)被曲线 所截的弦长_____
14. 椭圆 (θ为参数)的左焦点的坐标是__________.
15. 已知直线l的斜率为k=-1,经过点M 0 (2,-1),点M在直线上,以 的数量t为参数,则直线l的参数方程为_____________.
16. 已知圆的渐开线的参数方程是 ( φ 为参数),则此渐开线对应的基圆的直径是___________,当参数 φ = 时对应的曲线上的点的坐标为___________.
三、 解答题(每小题14分)
17. 已知A(10,-1,6),B(4,1,9),C(2,4,3),求证:△ABC是等腰三角形.
18. 【题文】(12分)已知点 的坐标分别为 ,直线 相交于点 ,且它们的斜率之积是 ,试讨论点 的轨迹是什么。
19. 如图, m , n 是空间两条相交直线, l 1 , l 2 是与 m , n 都垂直的两条直线,直线 l 与 l 1 , l 2 都相交,求证:∠1=∠2.
20. 已知x>0,y>0,求证: .
21. 已知 x , y ∈ R ,若 x 2 +2 x +(2 y + x )i和3 x -( y +1)i是共轭复数,求复数 z = x + y i和 .
答案解析部分(共有 21 道题的解析及答案)
一、选择题
1、 【答案】C
【解析】由题意可得 =10, =40.5,所以 = +2 =40.5+2×10=60.5,所以 ,当 =72时, ,解得 x ≈-6,故选C.
考点:回归分析
2、 思路解析: 回归分析是对两个变量之间的相关关系的一种分析,而相关关系是一种不确定的关系,通过回归分析可以确定两个变量之间具有的近似关系;而独立性检验是对两个变量之间是否具有某种关系的分析,并且可以分析这两个变量在多大程度上具有这种关系,但不能100%肯定这种关系.
答案: C
3、 【答案】B
【解析】
试题分析:因为 ,所以 , 是等比数列
首项 +2=4,公比q=2
∴ 等于 ,故选B。
考点:本题主要考查演绎推理的意义,等比数列通项公式。
点评:从一般性的原理出发,推出某个特殊情况下的结论,我们把这种推理称为演绎推理。简言之,演绎推理是由一般到特殊的推理。演绎推理也称为逻辑推理。
4、 解析: ∵ ,由向量加法的平行四边形法则知 P 为 AC 中点.
如图.
∴ .
答案: B
5、 【答案】D
【解析】 ,所以a=3,选D.
6、 【答案】A
【解析】
试题分析: ,因此复数 在复平面上对应的点位于第一象限.
考点:1.复数的几何意义;2.复数的四则运算.
7、
8、B
9、 解析: 由于点 P 的纵坐标是0,则点 P 在 xOz 平面内.
答案: C
10、 【答案】A
【解析】
试题分析: , ,则 点的直角坐标是 。故选A。
考点:极坐标与直角坐标的转换
点评:极坐标转换为直角坐标的公式是 ,而直角坐标转换为极坐标的公式是 。
11、 解析 : 圆的方程可化为ρ=2cos(θ- ).
这是ρ=2rcos(θ-θ 0 )的形式,它的圆心为O 1 (r,θ 0 ),本题也可化为直角坐标方程求解.
答案 : A
12、 【答案】
【解析】略
二、填空题
13、 【答案】
【解析】因为曲线
所以
所以曲线的直角坐标方程为 ,即
所以曲线为圆心 ,半径为 的园;
由直线的参数方程 ,消去参数 得
圆心 到直线 的距离
所以直线被园的截得弦长等于
故答案为 .
【考点】直线的参数方程;极坐标方程;直线与园相交的弦长问题.
14、 解析 : a=4,b=3,∴c= .∴坐标为( ,0).
答案 : ( ,0).
15、 思路解析: ∵直线的斜率k=-1,∴倾斜角α= .因此得cosα= ,sinα= .代入参数方程的标准形式即可.
答案: (t为参数).
16、 解析: 圆的渐开线的参数方程由圆的半径唯一确定,从方程不难看出基圆的半径为1,故直径为2.求当 φ = 时对应的坐标只需把 φ = 代入曲线的参数方程, x = ,由此可得对应的坐标为( ).
答案: 2 ( ).
三、解答题
17、 分析: 已知三角形的顶点坐标时,可以利用两点的距离公式判断该三角形的形状.
∴|AB|=|BC|.
∴△ABC是等腰三角形.
18、 【答案】(1)当 时, 的轨迹是圆;
(2)当 时, 的轨迹是椭圆;
(3)当 时, 的轨迹是双曲线
【解析】
试题分析:设 的坐标为 ,
由直线 的斜率之积是 ,得: , …6分
所以当 时,方程变为 ,为圆; …8分
当 时, 的轨迹是椭圆; …10分
当 时, 的轨迹是双曲线. …12分
考点:本小题主要考查了直接法求轨迹方程,并根据参数的范围判断轨迹是什么图形.
点评:掌握好圆、椭圆、双曲线、抛物线等圆锥曲线的标准方程的特点,是解决此类问题的关键.
19、证明:因为 m , n 是两条相交直线,所以直线 m , n 确定一个平面 α ,如图.因为 l 1 ⊥ m , l 1 ⊥ n ,所以 l 1 ⊥ α .同理 l 2 ⊥ α .所以 l 1 ∥ l 2 .所以 l 1 , l 2 确定一个平面 β ,又 l 与 l 1 , l 2 都相交,所以 l ? β .在同一平面 β 内,由 l 1 ∥ l 2 ,得∠1=∠2.
20、【探究】本题若直接用综合法,则不易发现与已知不等式的关系,因而可试用分析法.
【证明】要证明
只需证:(x 2 +y 2 ) 3 >(x 3 +y 3 ) 2 ,
即证:x 3 +3x 4 y 2 +3x 2 y 4 +y 6 >x 6 +2x 3 y 3 +y 6 ,
即证:3x 4 y 2 +3x 2 y 4 >2x 3 y 3 .
∵x>0,y>0,∴x 2 y 2 >0,
即证:3x 2 +3y 2 >2xy,
∵3x 2 +3y 2 >x 2 +y 2 ≥2xy,
∴3x 2 +3y 2 >2xy成立,
【规律总结】用分析法思考数学问题的顺序可表示为:(对于命题“若A则D”)
分析法的思考顺序是执果索因的顺序,是从D上溯寻其论据,如C、C 1 、C 2 等,再寻求C、C 1 、C 2 的论据,如B、B 1 、B 2 、B 3 、B 4 等等,继而寻求B、B 1 、B 2 、B 3 、B 4 的论据,如果其中之一B的论据恰为已知条件,于是命题已经得证.
21、分析:根据共轭复数的概念,将复数问题实数化,从而求得 x , y .
解:若两个复数 a + b i与 c + d i共轭,则 a = c ,且 b =- d .
由此可得到关于 x , y 的方程组
解得 或
所以 或