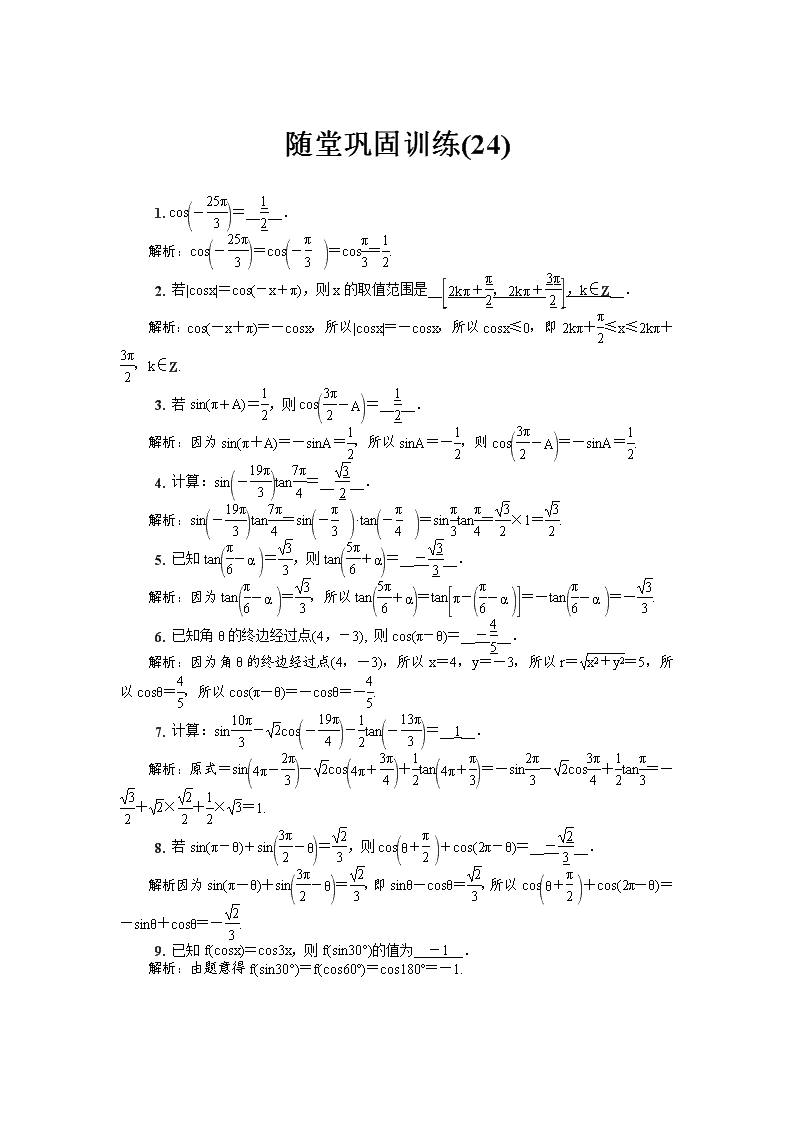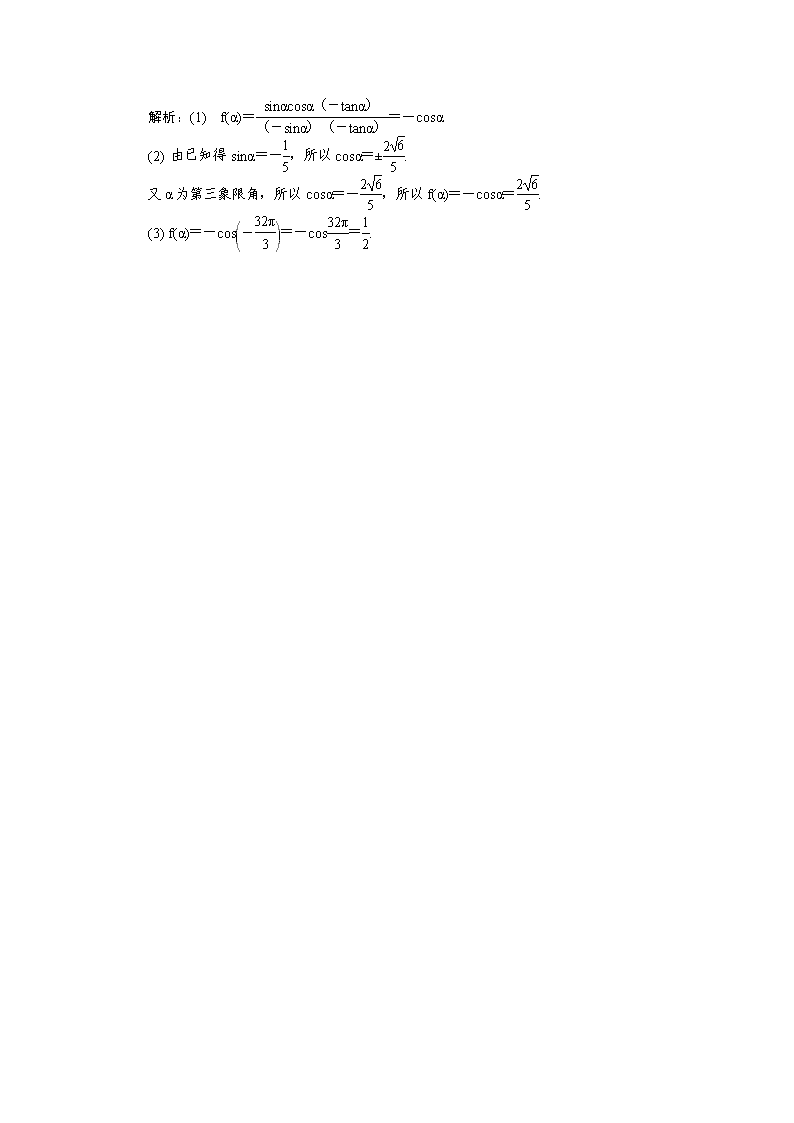【数学】2020届一轮复习人教A版第24课三角函数的诱导公式作业（江苏专用） 3页

随堂巩固训练(24)‎ ‎ 1. cos＝____．‎ 解析：cos＝cos＝cos＝.‎ ‎ 2. 若|cosx|＝cos(－x＋π)，则x的取值范围是__，k∈Z__．‎ 解析：cos(－x＋π)＝－cosx，所以|cosx|＝－cosx，所以cosx≤0，即2kπ＋≤x≤2kπ＋，k∈Z.‎ ‎ 3. 若sin(π＋A)＝，则cos＝____．‎ 解析：因为sin(π＋A)＝－sinA＝，所以sinA＝－，则cos＝－sinA＝.‎ ‎ 4. 计算：sintan＝____．‎ 解析：sintan＝sin·tan＝sintan＝×1＝.‎ ‎ 5. 已知tan＝，则tan＝__－__．‎ 解析：因为tan＝，所以tan＝tan＝－tan＝－.‎ ‎ 6. 已知角θ的终边经过点(4，－3), 则cos(π－θ)＝__－__．‎ 解析：因为角θ的终边经过点(4，－3)，所以x＝4，y＝－3，所以r＝＝5，所以cosθ＝，所以cos(π－θ)＝－cosθ＝－.‎ ‎ 7. 计算：sin－cos－tan＝__1__．‎ 解析：原式＝sin－cos＋tan＝－sin－cos＋tan＝－＋×＋×＝1.‎ ‎ 8. 若sin(π－θ)＋sin＝，则cos＋cos(2π－θ)＝__－__．‎ 解析：因为sin(π－θ)＋sin＝，即sinθ－cosθ＝，所以cos＋cos(2π－θ)＝－sinθ＋cosθ＝－.‎ ‎ 9. 已知f(cosx)＝cos3x，则f(sin30°)的值为__－1__．‎ 解析：由题意得f(sin30°)＝f(cos60°)＝cos180°＝－1.‎ ‎10. 若tanθ＝2，则＝__－2__．‎ 解析：原式＝＝＝－2.‎ ‎11. 已知函数f(x)＝g(x)＝求g＋f＋g＋f的值．‎ 解析：因为g＝，f＝f＋1＝sin＋1＝1－，‎ g＝g＋1＝cos＋1＝1＋，‎ f＝f＋1＝sin＋1＝1－，‎ 所以g＋f＋g＋f＝＋1－＋1＋＋1－＝3.‎ ‎12. (1) 化简：；‎ ‎(2) 化简：，k∈Z.‎ 解析：(1) 原式＝＝－tanα.　‎ ‎ (2) 当k＝2n(n∈Z)时，‎ 原式＝＝＝＝‎ ‎－＝－1；‎ 当k＝2n＋1(n∈Z)时，‎ 原式＝＝＝＝－1.‎ 综上所述，当k∈Z时，原式＝－1.‎ ‎13. 已知α为第三象限角，且f(α)＝.‎ ‎(1) 化简f(α)；‎ ‎(2) 若cos＝，求f(α)的值；‎ ‎(3) 若α＝－，求f(α)的值．‎ 解析：(1) f(α)＝＝－cosα.‎ ‎(2) 由已知得sinα＝－，所以cosα＝±.‎ 又α为第三象限角，所以cosα＝－，所以f(α)＝－cosα＝.‎ ‎(3) f(α)＝－cos＝－cos＝.‎