- 268.00 KB
- 2021-04-13 发布
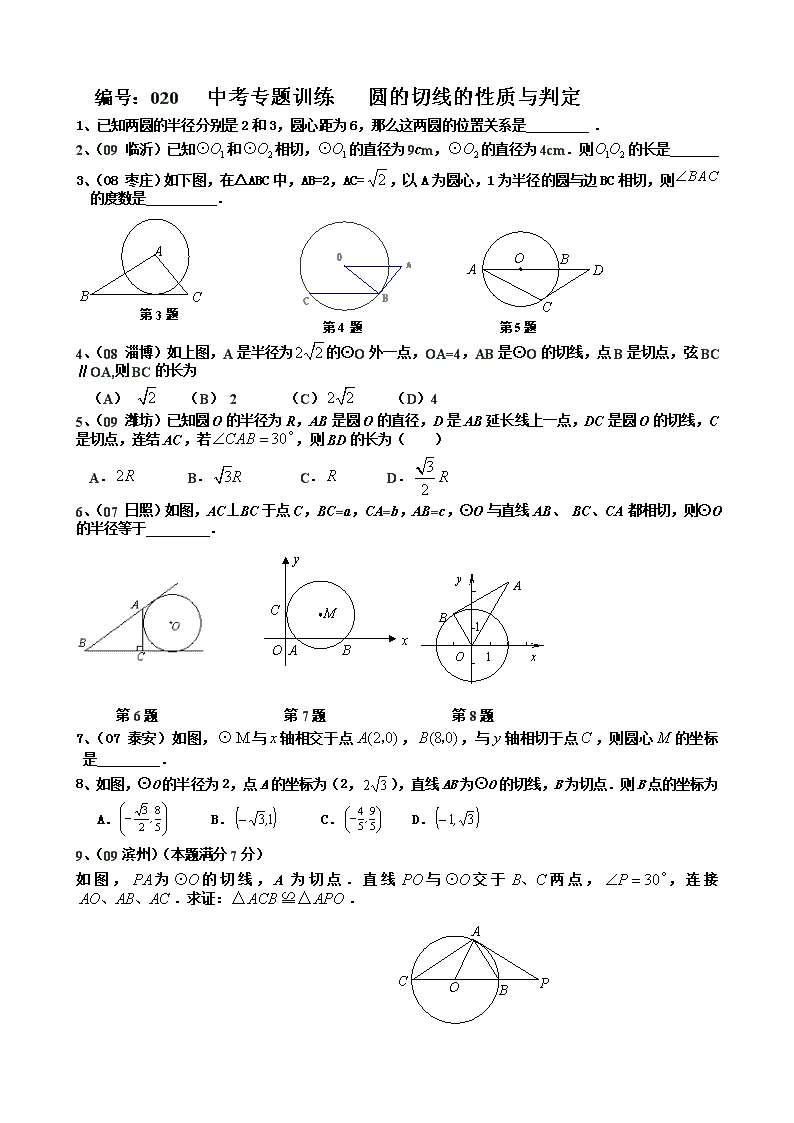
编号:020 中考专题训练 圆的切线的性质与判定
1、已知两圆的半径分别是2和3,圆心距为6,那么这两圆的位置关系是 .
2、(09 临沂)已知和相切,的直径为9cm,的直径为4cm.则的长是
3、(08 枣庄)如下图,在△ABC中,AB=2,AC=,以A为圆心,1为半径的圆与边BC相切,则的度数是 .
O
B
C
D
A
A
B
C
第3题图
第4 题 第5题
4、(08 淄博)如上图,A是半径为的⊙O外一点,OA=4,AB是⊙O的切线,点B是切点,弦BC∥OA,则BC的长为
(A) (B) 2 (C) (D)4
5、(09 潍坊)已知圆O的半径为R,AB是圆O的直径,D是AB延长线上一点,DC是圆O的切线,C是切点,连结AC,若,则BD的长为( )
A. B. C. D.
6、(07 日照)如图,AC⊥BC于点C,BC=a,CA=b,AB=c,⊙O与直线AB、 BC、CA都相切,则⊙O的半径等于 .
y
x
M
B
A
O
C
x
y
O
1
1
B
A
第6题 第7题 第8题
7、(07 泰安)如图,与轴相交于点,,与轴相切于点,则圆心的坐标是 .
8、如图,⊙O的半径为2,点A的坐标为(2,),直线AB为⊙O的切线,B为切点.则B点的坐标为
A. B. C. D.
9、(09滨州)(本题满分7分)
如图,为的切线,A为切点.直线与交于两点,,连接.求证:.
A
O
B
P
C
A
D
B
C
E
F
G
O
10、(09 聊城)(10分)如图,⊙O是△ABC的内切圆,与AB、BC、CA分别相切于点D、E、F,∠DEF=45º.连接BO并延长交AC于点G,AB=4,AG=2 (1)求∠A的度数;(2)求⊙O的半径.
11、(07 日照)如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.
(1)求证:点E是边BC的中点;
(2)若EC=3,BD=,求⊙O的直径AC的长度;
(3)若以点O,D,E,C为顶点的四边形是正方形,试判断△ABC的形状,并说明理
编号:021
A
G
F
E
C
B
O
(第12题)
12、(07 泰安)(本小题满分9分)
如图,在中,,以为直径的圆交于点,交于点,过点作,垂足为.
(1)求证:为的切线;
(2)若过点且与平行的直线交的延长线于点,连结.当是等边三角形时,求的度数.
13、(08 泰安)(本小题满分10分)
B
D
C
E
A
O
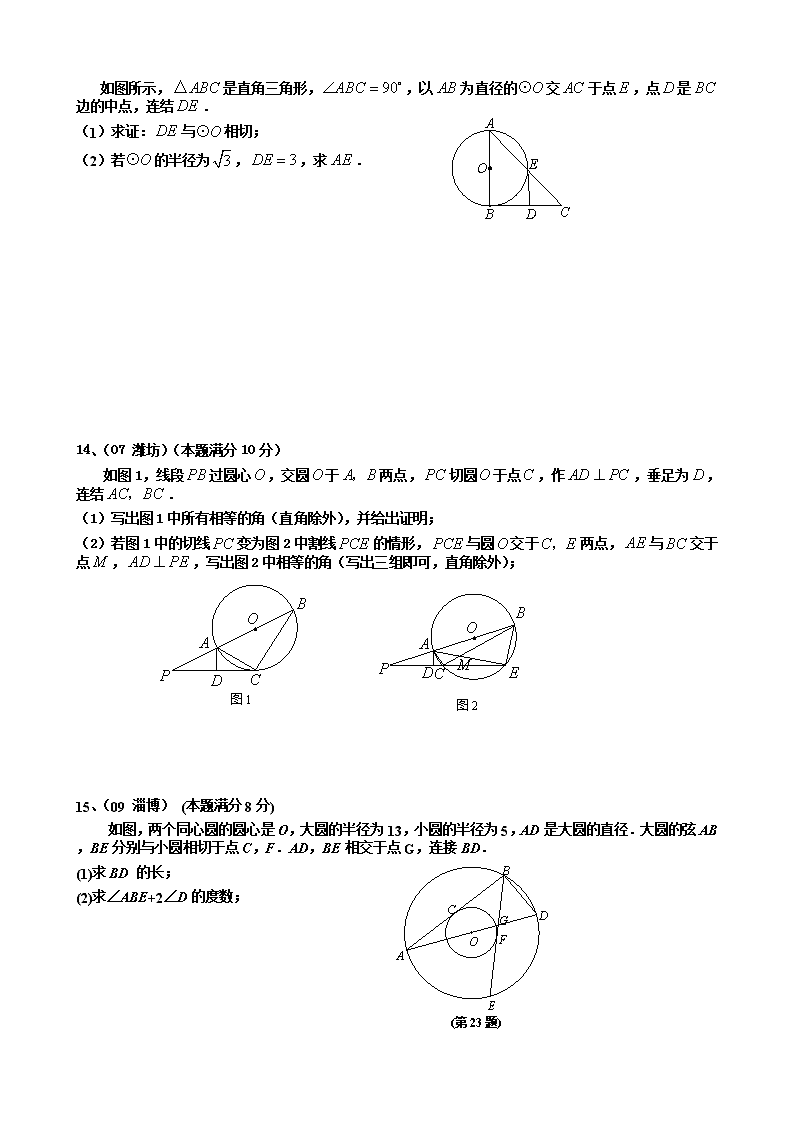
如图所示,是直角三角形,,以为直径的交于点,点是边的中点,连结.
(1)求证:与相切;
(2)若的半径为,,求.
14、(07 潍坊)(本题满分10分)
如图1,线段过圆心,交圆于两点,切圆于点,作,垂足为,连结.
(1)写出图1中所有相等的角(直角除外),并给出证明;
(2)若图1中的切线变为图2中割线的情形,与圆交于两点,与交于点,,写出图2中相等的角(写出三组即可,直角除外);
图1
图2
15、(09 淄博) (本题满分8分)
A
C
B
D
G
F
E
O
(第23题)
如图,两个同心圆的圆心是O,大圆的半径为13,小圆的半径为5,AD是大圆的直径.大圆的弦AB,BE分别与小圆相切于点C,F.AD,BE相交于点G,连接BD.
(1)求BD 的长;
(2)求∠ABE+2∠D的度数;
相关文档
- 深圳中考真题2021-04-13 00:44:536页
- 2020学年高中语文 第一单元 以国家2021-04-13 00:44:517页
- 最新中考英语阅读理解50篇[精品资2021-04-13 00:44:4781页
- 2018-2019学年黑龙江省鸡西市第十2021-04-13 00:44:4615页
- 部编版七年级上册语文期末复习专题2021-04-13 00:44:4113页
- 六年级下册数学试题-期末全真模拟2021-04-13 00:44:344页
- 2019届二轮复习(理)第九章平面解析几2021-04-13 00:44:2211页
- 中考数学贵州安顺—解析版2021-04-13 00:44:1220页
- 六年级下册数学试题-小升初专题培2021-04-13 00:43:555页
- 2019届中考语文 文言文专项复习十2021-04-13 00:43:237页