2020版高考数学二轮复习 专题五 立体几何 专题突破练16 空间中的垂直与几何体的体积 文 9页

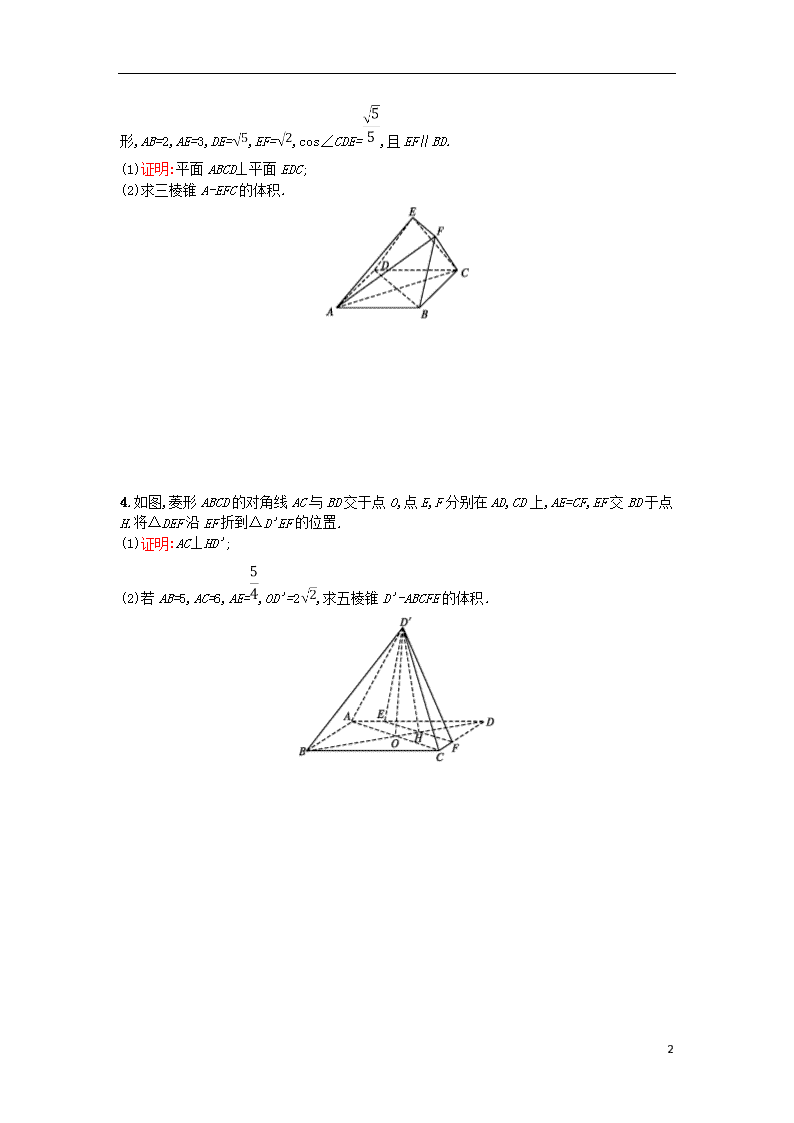
专题突破练16　空间中的垂直与几何体的体积 ‎1.(2018江苏卷,15)在平行六面体ABCD-A1B‎1C1D1中,AA1=AB,AB1⊥B‎1C1.‎ 求证:(1)AB∥平面A1B‎1C;‎ ‎(2)平面ABB‎1A1⊥平面A1BC.‎ ‎2.如图,四面体ABCD中,△ABC是正三角形,AD=CD.‎ ‎(1)证明:AC⊥BD;‎ ‎(2)已知△ACD是直角三角形,AB=BD,若E为棱BD上与D不重合的点,且AE⊥EC,求四面体ABCE与四面体ACDE的体积比.‎ ‎3.(2018江西南昌三模,文18)如图,多面体ABCDEF中,四边形ABCD 9‎ 为正方形,AB=2,AE=3,DE=,EF=,cos∠CDE=,且EF∥BD.‎ ‎(1)证明:平面ABCD⊥平面EDC;‎ ‎(2)求三棱锥A-EFC的体积.‎ ‎4.如图,菱形ABCD的对角线AC与BD交于点O,点E,F分别在AD,CD上,AE=CF,EF交BD于点H.将△DEF沿EF折到△D'EF的位置.‎ ‎(1)证明:AC⊥HD';‎ ‎(2)若AB=5,AC=6,AE=,OD'=2,求五棱锥D'-ABCFE的体积.‎ 9‎ ‎5.(2018河南郑州三模,文19)如图,四棱锥E-ABCD中,AD∥BC,AD=AB=AE=BC=1,且BC⊥底面ABE,M为棱CE的中点,‎ ‎(1)求证:直线DM⊥平面CBE;‎ ‎(2)当四面体D-ABE的体积最大时,求四棱锥E-ABCD的体积.‎ ‎6.如图,在三棱台ABC-DEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.‎ ‎(1)求证:BF⊥平面ACFD;‎ ‎(2)求直线BD与平面ACFD所成角的余弦值.‎ ‎7.(2018全国卷3,文19)如图,矩形ABCD所在平面与半圆弧所在平面垂直,M是上异于C,D的点.‎ 9‎ ‎(1)证明:平面AMD⊥平面BMC;‎ ‎(2)在线段AM上是否存在点P,使得MC∥平面PBD?说明理由.‎ ‎8.如图(1),在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC=2,AD=6,CE⊥AD于点E,把△DEC沿CE折到△D'EC的位置,使D'A=2,如图(2).若G,H分别为D'B,D'E的中点.‎ ‎(1)求证:GH⊥D'A;‎ ‎(2)求三棱锥C-D'BE的体积.‎ 9‎ 参考答案 专题突破练16　空间中的垂直与 几何体的体积 ‎1.证明 (1)在平行六面体ABCD-A1B‎1C1D1中,AB∥A1B1.‎ 因为AB⊄平面A1B‎1C,A1B1⊂平面A1B‎1C,所以AB∥平面A1B‎1C.‎ ‎(2)在平行六面体ABCD-A1B‎1C1D1中,四边形ABB‎1A1为平行四边形.‎ 又因为AA1=AB,所以四边形ABB‎1A1为菱形,因此AB1⊥A1B.‎ 又因为AB1⊥B‎1C1,BC∥B‎1C1,‎ 所以AB1⊥BC.‎ 又因为A1B∩BC=B,A1B⊂平面A1BC,BC⊂平面A1BC,‎ 所以AB1⊥平面A1BC.‎ 因为AB1⊂平面ABB‎1A1,‎ 所以平面ABB‎1A1⊥平面A1BC.‎ ‎2.(1)证明 取AC的中点O,连接DO,BO.‎ 因为AD=CD,所以AC⊥DO.‎ 又由于△ABC是正三角形,‎ 所以AC⊥BO.‎ 从而AC⊥平面DOB,故AC⊥BD.‎ ‎(2)解 连接EO.‎ 由(1)及题设知∠ADC=90°,‎ 所以DO=AO.‎ 在Rt△AOB中,BO2+AO2=AB2.‎ 又AB=BD,所以BO2+DO2=BO2+AO2=AB2=BD2,故∠DOB=90°.‎ 9‎ 由题设知△AEC为直角三角形,‎ 所以EO=AC.‎ 又△ABC是正三角形,且AB=BD,‎ 所以EO=BD.‎ 故E为BD的中点,从而E到平面ABC的距离为D到平面ABC的距离的,四面体ABCE的体积为四面体ABCD的体积的,即四面体ABCE与四面体ACDE的体积之比为1∶1.‎ ‎3.(1)证明 ∵AB=2,AE=3,DE=,由勾股定理得AD⊥DE.又正方形ABCD中AD⊥DC,且DE∩DC=D,‎ ‎∴AD⊥平面EDC.‎ ‎∵AD⊂面ABCD,‎ ‎∴平面ABCD⊥平面EDC.‎ ‎(2)解 由已知cos∠CDE=,连接AC交BD于G.‎ 作OE⊥CD于O,‎ 则OD=DE·cos∠CDE=1,OE=2.‎ 又由(1)知,平面ABCD⊥平面EDC,平面ABCD∩平面EDC=CD,‎ OE⊂平面EDC,得OE⊥面ABCD.‎ 由EF∥BD,EF=,知四边形DEFG为平行四边形,即DE∥FG,‎ 而VA-EFC=VE-AFC,进而VA-EFC=VE-AFC=VD-AFC=VF-ADC.又由EF∥BD,VF-ADC=VE-ADC=×2×2×2=,所以,三棱锥A-EFC的体积为.‎ ‎4.(1)证明 由已知得AC⊥BD,AD=CD.‎ 又由AE=CF得,故AC∥EF.由此得EF⊥HD,EF⊥HD',所以AC⊥HD'.‎ 9‎ ‎(2)解 由EF∥AC得.‎ 由AB=5,AC=6得DO=BO==4.‎ 所以OH=1,D'H=DH=3.‎ 于是OD'2+OH2=(2)2+12=9=D'H2,故OD'⊥OH.由(1)知AC⊥HD',‎ 又AC⊥BD,BD∩HD'=H,‎ 所以AC⊥平面BHD',于是AC⊥OD'.又由OD'⊥OH,AC∩OH=O,‎ 所以,OD'⊥平面ABC.‎ 又由得EF=.‎ 五边形ABCFE的面积S=×6×8-×3=.‎ 所以五棱锥D'-ABCFE的体积V=×2.‎ ‎5.解 (1)∵AE=AB,设N为EB的中点,‎ ‎∴AN⊥EB.‎ 又BC⊥平面AEB,AN⊂平面AEB,‎ ‎∴BC⊥AN.‎ 又BC∩BE=B,∴AN⊥平面BCE.‎ ‎∵MN∥BC,MN=BC,‎ ‎∴AD