- 310.50 KB
- 2021-04-12 发布
2018-2019学年度第二学期高新部
高二重点班数学(文)期中考试试题
一、选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.若复数,则在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.计算的结果是 ( )
A.- B. C. D.
3.已知x与y之间的一组数据:
x
0
1
2
3
y
1
3
5
7
则y与x的线性回归方程为y=bx+a必过点 ( )
A .(2,2) B.(1,2) C.(1.5,4) D (1.5,0)
4.反证法证明命题:“一个三角形中不能有两个直角”的过程归纳为以下三个步骤:①,这与三角形内角和为相矛盾,不成立;②所以一个三角形中不能有两个直角;③假设三角形的三个内角A、B、C中有两个直角,不妨设;正确顺序的序号为 ( )
A.①②③ B.③①② C.①③② D.②③①
5.对相关系数r,下列说法正确的是 ( )
A.越大,线性相关程度越大
B.越小,线性相关程度越大
C.越大,线性相关程度越小,越接近0,线性相关程度越大
D.且越接近1,线性相关程度越大,越接近0,线性相关程度越小
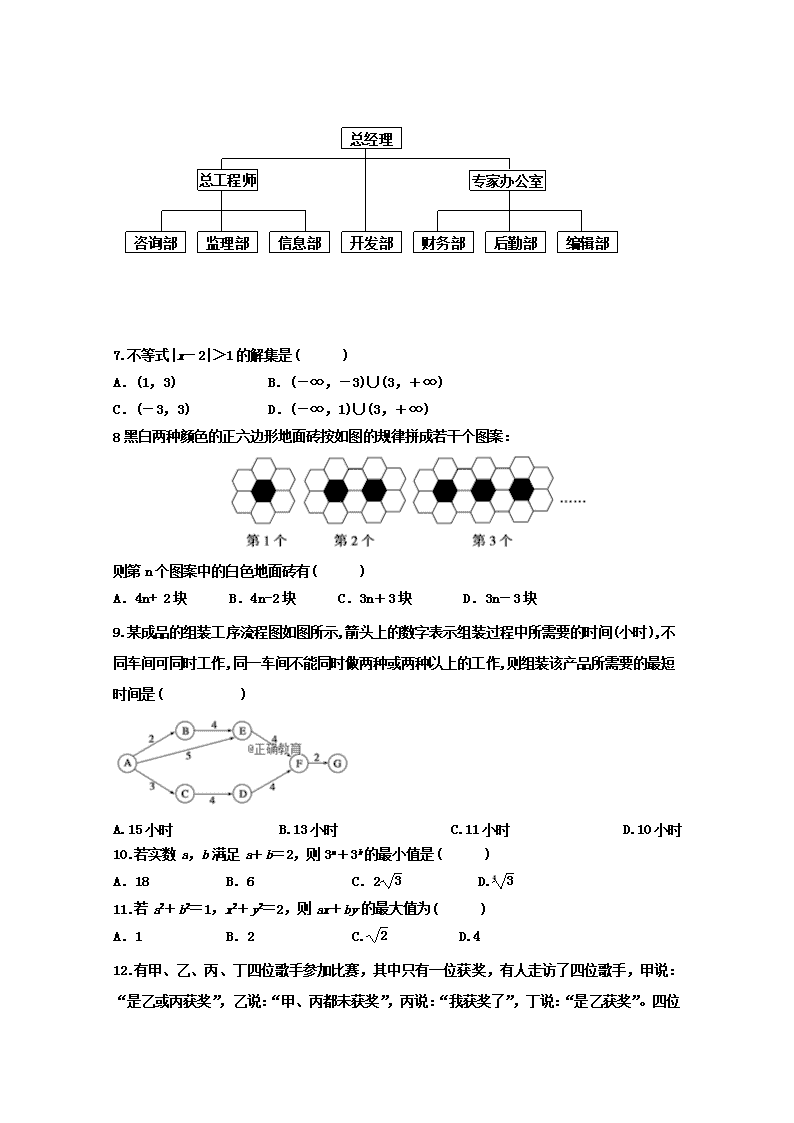
6.根据下面的结构图,总经理的直接下属是( )
A.总工程师和专家办公室 B.总工程师、专家办公室和开发部
C.开发部 D.总工程师、专家办公室和所有七个部
总经理
总工程师
专家办公室
咨询部
监理部
信息部
开发部
财务部
后勤部
编辑部
7.不等式|x-2|>1的解集是( )
A.(1,3) B.(-∞,-3)∪(3,+∞)
C.(-3,3) D.(-∞,1)∪(3,+∞)
8黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案:
则第n个图案中的白色地面砖有( )
A.4n+ 2块 B.4n-2块 C.3n+3块 D.3n-3块
9.某成品的组装工序流程图如图所示,箭头上的数字表示组装过程中所需要的时间(小时),不同车间可同时工作,同一车间不能同时做两种或两种以上的工作,则组装该产品所需要的最短时间是( )
A.15小时 B.13小时 C.11小时 D.10小时
10.若实数a,b满足a+b=2,则3a+3b的最小值是( )
A.18 B.6 C.2 D.
11.若a2+b2=1,x2+y2=2,则ax+by的最大值为( )
A.1 B.2 C. D.4
12.有甲、乙、丙、丁四位歌手参加比赛,其中只有一位获奖,有人走访了四位歌手,甲说:“是乙或丙获奖”,乙说:“甲、丙都未获奖”,丙说:“我获奖了”,丁说:“是乙获奖”
。四位歌手的话只有两名是对的,则获奖的歌手是( )
A.甲 B.乙 C.丙 D.丁
二、填空题(本大题共4小题,每题5分,共20分)
13.已知,若,则 .
14.给出四个条件:
①b>0>a,②0>a>b,③a>0>b,④a>b>0.能得出<成立的有________.(填序号)
15.若不等式|x-4|+|x-3|>a对一切实数x恒成立,则实数a的取值范围是________.
16.在平面直角坐标系中,以点为圆心,为半径的圆的方程为,类比圆的方程,请写出在空间直角坐标系中以点为球心,半径为的球的方程为
三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.)
17.(10分)实数m取什么数值时,复数分别是:
(1)实数? (2)虚数? (3)纯虚数?
18.(12分)甲乙两个班级均为40人,进行一门考试后,按学生考试成绩及格与不及格进行统计,甲班及格人数为36人,乙班及格人数为24人.
(1)根据以上数据建立一个的列联表;(2)试判断是否成绩与班级是否有关?
参考公式:;(10分)
P(K2>k)
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k
0.455
0.708
1.323
2.072
2.706
3.84
5.024
6.635
7.879
10.83
19.证明题(每小题6分共12分):
(1)求证:
(2)若,,求证:
20.(12分)做一个体积为32,高为2m的长方体纸盒,底面的长与宽取什么值时用纸最少?
21. (12分)某种产品的广告费用支出(万元)与销售额(万元)之间有如下的对应
2
4
5
6
8
30
40
60
50
70
数据:
(1)画出散点图;(2)求回归直线方程;
(3)据此估计广告费用为9万元时,销售收入的值.(10分)
参考公式:回归直线的方程,其中.
22..设函数f(x)=|x+1|-|x-2|.
(1)求不等式f(x)≥2的解集;
(2)若不等式f(x)≤|a-2|的解集为R,求实数a的取值范围.
试题答案
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
A
C
B
D
B
D
A
C
B
C
C
二、填空题:本大题共4小题,每小题5分,共20分.
13. -3 ; 14. ①②④ ;
15.(-∞,1) ; 16.
三、解答题:本大题共5小题,每小题8分,共40分.解答应写出文字说明、证明过程或演算步骤.
17.解:(1)当,即时,复数z是实数;……3分
(2)当,即时,复数z是虚数;……6分
(3)当,且时,即时,复数z 是纯虚数;
……10分
18.解:(1)2×2列联表如下:
不及格
及格
总计
甲班
4
36
40
乙班
16
24
40
总计
20
60
80
……6分
(2)
由,所以有99.5%的把握认为“成绩与班级有关系”
…12分
19. 解:(1)
只需证,因为56>50成立
成立 ……6分
(2)
20.解:设底面的长为xm,宽为ym,需用纸z
根据题意,有
因为体积为32 , 所以,,即
由基本不等式于不等式的性质,可得
,当且仅当时取等号
此时,,所以
所以,当长宽都是4时,用纸最少为64
21.解:(1)作出散点图如下图所示:
……3分
(2),,
,,.
,.
因此回归直线方程为; ……9分
(3)时,预报的值为(万元).……12分
22.解:(1)f(x)=
当x≤-1时,f(x)≥2不成立;
当-1<x<2时,由f(x)≥2得,2x-1≥2,
所以≤x<2.
当x≥2时,f(x)≥2恒成立.
所以不等式f(x)≥2的解集为. ……6分
(2)因为f(x)=|x+1|-|x-2|≤|(x+1)-(x-2)|=3,
所以|a-2|≥3.
所以a≥5或a≤-1.
所以a的取值范围是(-∞,-1]∪[5,+∞). ……12分