2018届二轮复习（理）规范答题示例6　空间中的平行与垂直关系课件（全国通用） 11页

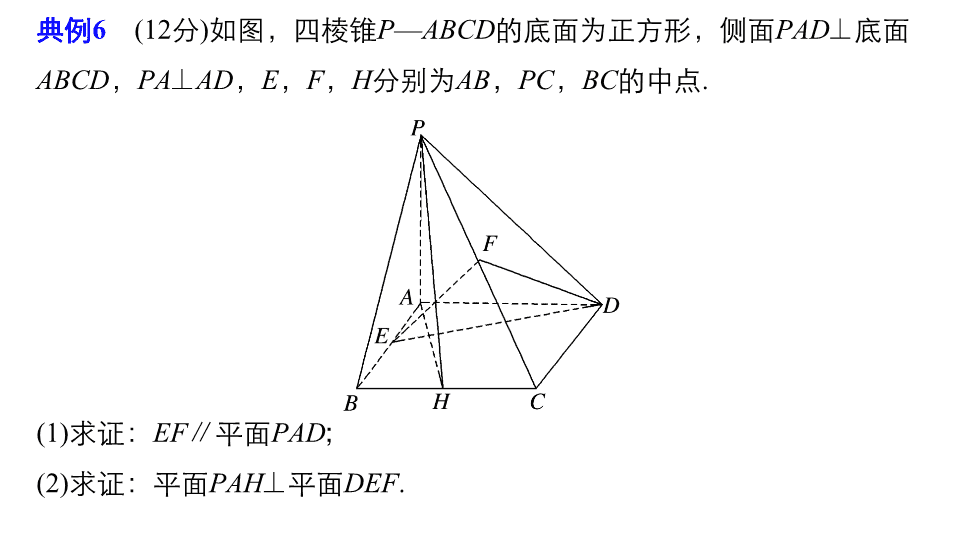
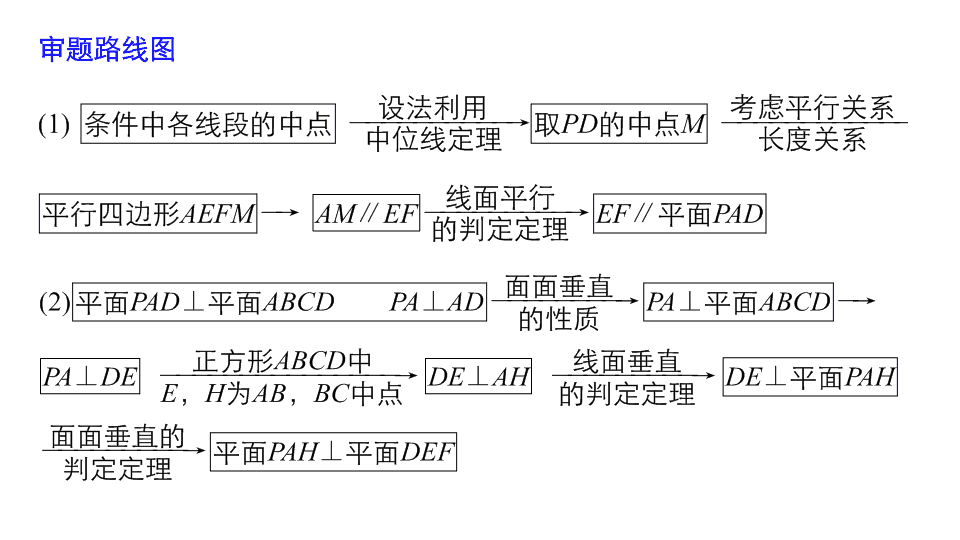
规范答题 示例 6 　 空间中的平行与垂直关系 典例 6 　 (12 分 ) 如图，四棱锥 P — ABCD 的底面为正方形，侧面 PAD ⊥ 底面 ABCD ， PA ⊥ AD ， E ， F ， H 分别为 AB ， PC ， BC 的中点 . (1) 求证： EF ∥ 平面 PAD ； (2) 求证：平面 PAH ⊥ 平面 DEF . 规 范 解 答 · 分 步 得 分 证明　 (1) 取 PD 的中点 M ，连接 FM ， AM . ∵ 在 △ PCD 中， F ， M 分别为 PC ， PD 的中点， ∴ AE ∥ FM 且 AE ＝ FM ， 则四边形 AEFM 为平行四边形， ∴ AM ∥ EF ， 4 分 ∵ EF ⊄ 平面 PAD ， AM ⊂ 平面 PAD ， ∴ EF ∥ 平面 PAD . 6 分 (2) ∵ 侧面 PAD ⊥ 底面 ABCD ， PA ⊥ AD ，侧面 PAD ∩ 底面 ABCD ＝ AD ， ∴ PA ⊥ 底面 ABCD ， ∵ DE ⊂ 底面 ABCD ， ∴ DE ⊥ PA . ∵ E ， H 分别为正方形 ABCD 边 AB ， BC 的中点， ∴ Rt △ ABH ≌ Rt △ DAE ， 则 ∠ BAH ＝ ∠ ADE ， ∴∠ BAH ＋ ∠ AED ＝ 90° ， ∴ DE ⊥ AH ， 8 分 ∵ PA ⊂ 平面 PAH ， AH ⊂ 平面 PAH ， PA ∩ AH ＝ A ， ∴ DE ⊥ 平面 PAH ， ∵ DE ⊂ 平面 EFD ， ∴ 平面 PAH ⊥ 平面 DEF . 12 分 构 建 答 题 模 板 第一步　 找线线： 通过三角形或四边形的中位线、平行四边形、等腰三角形的中线或线面、面面关系的性质寻找线线平行或线线垂直 . 第二步　 找线面： 通过线线垂直或平行，利用判定定理，找线面垂直或平行；也可由面面关系的性质找线面垂直或平行 . 第三步　 找面面： 通过面面关系的判定定理，寻找面面垂直或平行 . 第四步　 写步骤： 严格按照定理中的条件规范书写解题步骤 . 评分细则　 (1) 第 (1) 问证出 AE 綊 FM 给 2 分；通过 AM ∥ EF 证线面平行时，缺 1 个条件扣 1 分；利用面面平行证明 EF ∥ 平面 PAD 同样给分； (2) 第 (2) 问证明 PA ⊥ 底面 ABCD 时缺少条件扣 1 分；证明 DE ⊥ AH 时只要指明 E ， H 分别为正方形边 AB ， BC 的中点得 DE ⊥ AH 不扣分；证明 DE ⊥ 平面 PAH 只要写出 DE ⊥ AH ， DE ⊥ PA ，缺少条件不扣分 . 跟踪演练 6 　 如图，在三棱锥 V — ABC 中，平面 VAB ⊥ 平面 ABC ， △ VAB 为等边三角形， AC ⊥ BC 且 AC ＝ BC ＝ ， O ， M 分别为 AB ， VA 的中点 . (1) 求证： VB ∥ 平面 MOC ； 证明 证明 　 因为 O ， M 分别为 AB ， VA 的中点， 所以 OM ∥ VB ， 又因为 VB ⊄ 平面 MOC ， OM ⊂ 平面 MOC ， 所以 VB ∥ 平面 MOC . (2) 求证：平面 MOC ⊥ 平面 VAB ； 证明　 因为 AC ＝ BC ， O 为 AB 的中点， 所以 OC ⊥ AB . 又因为平面 VAB ⊥ 平面 ABC ，平面 VAB ∩ 平面 ABC ＝ AB ， 且 OC ⊂ 平面 ABC ， 所以 OC ⊥ 平面 VAB . 又 OC ⊂ 平面 MOC ， 所以平面 MOC ⊥ 平面 VAB . 证明 (3) 求三棱锥 V — ABC 的体积 . 所以 AB ＝ 2 ， OC ＝ 1 ， 又因为 OC ⊥ 平面 VAB . 又因为三棱锥 V — ABC 的体积与三棱锥 C — VAB 的体积相等， 解答