THUSSAT2019年9月诊断性测试文科数学试卷 8页

中学生标准学术能力诊断性测试 2019 年 9 月测试 文科数学试卷 本试卷共 150 分，考试时间 120 分钟。 一、选择题：本大题共 12 小题，每小题 5 分，共 60 分．在每小题给出的四个选项中，只有一项是 符合题目要求的． 1．已知集合 { 1, 0 ,1}A =− ， { | | 1|, }B y y x x A= = +  ，则 AB= A． { 1, 0}− B． { 0,1} C． { 1,1}− D． { 1, 0 ,1}− 2．已知复数 1 2 i 3iz += − （其中 i 为虚数单位），则 ||z = A． 2 2 B． 1 2 C． 26 10 D． 74 10 3．若向量 ， 满足 ， ，且 ，则向量 ， 的夹角为 A． B． C． D． 4．为得到函数 πcos(2 )3yx=−的图象，只需将函数 πsin(2 )3yx=+的图象 A．向左平移 π 6 个长度单位 B．向右平移 π 6 个长度单位 C．向左平移 π 12 个长度单位 D．向右平移 π 12 个长度单位 5．阅读算法流程图，运行相应的程序，则输出的 k 是 A． 5 B． 6 C． 7 D． 8 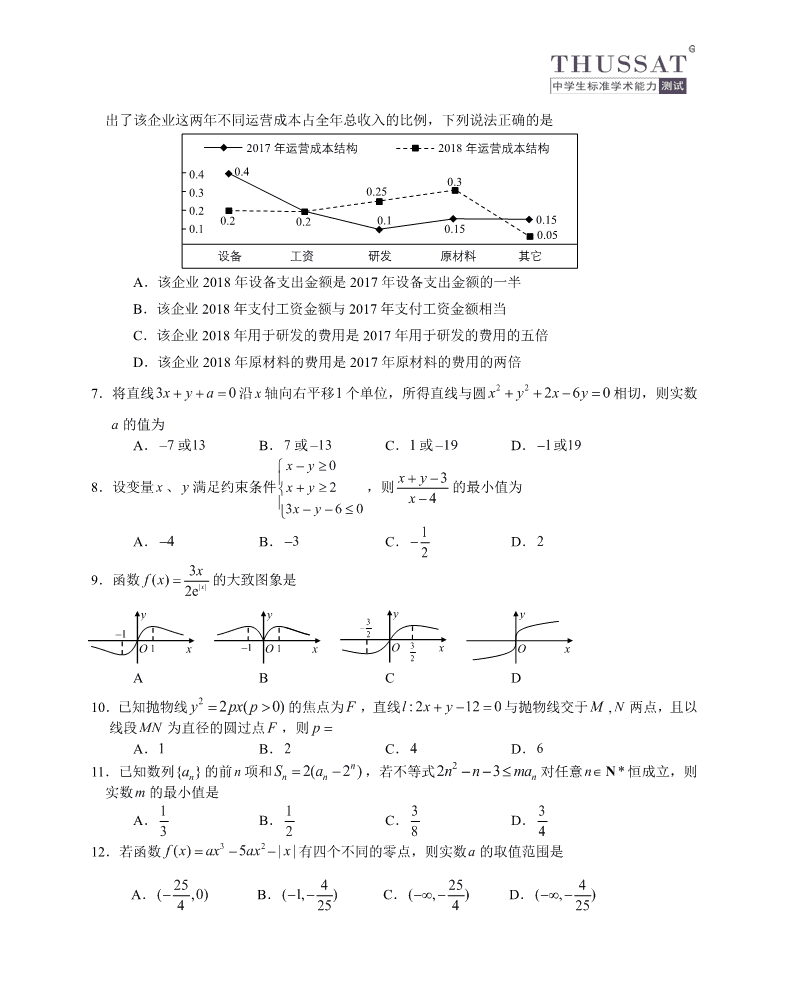6．某企业引进现代化管理体制，生产效益明显提高．2018 年全年总收入与 2017 年全年总收入相比 增长了一倍，实现翻番．同时该企业的各项运营成本也随着收入的变化发生了相应变化．下图给 a b | | 1 =a | | 2 =b | 3 | 19−=ab a b 30  60 120  150  （第 5 题图） 结束 开始 输出 k 是 0S  100S = 2kSS=− 1kk=+ 1k = 否 出了该企业这两年不同运营成本占全年总收入的比例，下列说法正确的是 A．该企业 2018 年设备支出金额是 2017 年设备支出金额的一半 B．该企业 2018 年支付工资金额与 2017 年支付工资金额相当 C．该企业 2018 年用于研发的费用是 2017 年用于研发的费用的五倍 D．该企业 2018 年原材料的费用是 2017 年原材料的费用的两倍 7．将直线30x y a+ + = 沿 x 轴向右平移1个单位，所得直线与圆 222 6 0x y x y+ + − = 相切，则实数 a 的值为 A． 7− 或 13 B． 7 或 13− C．1或 19− D． 1− 或 19 8．设变量 x 、 y 满足约束条件 0 2 3 6 0 xy xy xy −  +  − −  ，则 3 4 xy x +− − 的最小值为 A． 4− B． 3− C． 1 2− D． 2 9．函数 || 3() 2e x xfx= 的大致图象是 A B C D 10．已知抛物线 2 2 ( 0)y px p=的焦点为 F ，直线 : 2 12 0l x y+ − = 与抛物线交于 M , N 两点，且以 线段 MN 为直径的圆过点 F ，则 p = A．1 B． 2 C． 4 D． 6 11．已知数列{}na 的前 n 项和 2( 2 )n nnSa=−，若不等式 223nn n ma− −  对任意 *nN 恒成立，则 实数 m 的最小值是 A． 1 3 B． 1 2 C． 3 8 D． 3 4 12．若函数 32( ) 5 | |f x ax ax x= − − 有四个不同的零点，则实数 a 的取值范围是 x O y 1 1− x O y 11− x O y 设备 工资 研发 原材料 其它 0.1 0.2 0.3 0.4 0.4 0.2 0.2 0.1 0.25 0.3 0.15 0.05 0.15 2017 年运营成本结构 2018 年运营成本结构 y x O 3 2 3 2− A． ( 25 ,0)4− B． 1, ) 5( 4 2−− C． 5,)4( 2−− D． ,)25( 4−− 二、填空题：本大题共 4 小题，每小题 5 分，共 20 分． 13．在区间 [1, 1 6 ] 上随机选取一个实数 x ，则事件“ 3l o g 2 0x −”发生的概率为 ． 14．设函数 1, 1() 2 e , 1 x xxfx x  −=  − ，则使1 ( ) 2fx成立的 x 的取值范围是 ． 15．若双曲线 22 221( 0, 0)xy abab− =   的右焦点 ( ,0 )Fc ，右顶点 A 到一条渐近线的距离为 1 2 c ，则双 曲线的离心率为 ． 16．长方体 1111A B C D A B C D− 中，若 2AD = , 1 4CD = ，则当 1A D A C+ 最大时，三棱锥 1D A C D− 的 体积为 ． 三、解答题：共 70 分．解答应写出文字说明、证明过程或演算步骤．第 17~21 题为必考题，每个试 题考生都必须作答．第 22、23 题为选考题，考生根据要求作答． （一）必考题：60 分． 17．（12 分）在△ ABC 中， a , b , c 分别为角 A , B , C 的对边，且 cos 5 cos A c a Bb −= , π 4C = ． （1）求 c os A 的值； （2）若 5b = ，求△ ABC 的面积 S ． 18．（12 分）某高中学校决定开展“数学知识竞赛”活动，各班 级都进行了选拔，高三一班全体同学都参加了考试，将他们的 分数进行统计，并作出如右图的频率分布直方图和分数的茎叶 图（ 其中，茎叶图中仅列出了得分在 [ 5 0 ,6 0 ) ，[90 ,100] 的数据）． （1）求高三一班学生的总数和频率分布直方图中 a 、 b 的值； （2）在高三一班学生中，从竞赛成绩在 80 分以上（含 80 分）的 学生中随机抽取 2 名学生参加学校“数学知识竞赛”，求所抽 取的 2 名学生中至少有一人得分在[90,100] 内的概率． 频率/组距 0.040 b 0.010 0.016 a 成绩 50 60 70 80 90 100 5 1 2 2 4 6 6 7 7 6 7 8 9 1 2 4 19．（12 分）如图，四棱锥 P ABCD− 的底面为平行四边形，AB 为半圆的直径，D 在半圆上，PD ⊥ 平面 ABCD ，且 1PD AD==, 2AB = ， E 是 PC 的中点． （1）求证： //PA 平面 BDE ； （2）求点C 到平面 BDE 的距离． E B D A C P （第 19 题图） 20．（12 分）已知椭圆 的左焦点 1F ，直线 与 轴交于点 ， 且与椭圆交于 , 两点， 为椭圆的右顶点， 在 轴上的射影恰为 1F ． （1）求椭圆 的方程； （2） 为椭圆 在第一象限部分上一点，直线 MP 与椭圆交于另一点 N ，若 ， 求  的取值范围． 22 22: 1( 0)xyE a bab+ =   :l 2 3 6 0xy− − = y P A B A B x E M E :PMAPBNSS = 21．（12 分）设 , 为函数 图象上相异两点，且 , 的横坐标之积为常数 ，若 在 , 两点处的切线存在交点，则称这个交点为函数 的“ 点”． （1）求函数 的“ 点”的纵坐标的取值范围； （2）判断函数 的“ 点”在哪个象限，并说明理由． A B ()y f x= A B ( 0)kk ()y f x= A B ()fx ()Sk 3()f x x= (2)S ( ) l nf x x = ( 1 )S （二）选考题：共 10 分．请考生在第 22,23 题中任选一题作答，如果多做，则按所做的第一题计 分．作答时请写清题号． 22．[选修 4—4：坐标系与参数方程选讲]（10 分） 在平面直角坐标系中，曲线 22 1 : 4 0C x y x+ − = ，曲线 2 2cos : 3sin x C y   = = （  为参数），以坐标原点 O 为极点， x 轴非负半轴为极轴建立极坐标系． （1）求曲线 1C ， 2C 的极坐标方程； （2）在极坐标系中，射线 π 3 = 与 1C , 2C 分别交于 A , B 两点（异于极点 O ），定点 (5,0)M ，求△ MAB 的面积． 23．[选修 4—5：不等式选讲]（10 分） 已知函数 ( ) | 3 1| 2 | 1|f x x x= − − + ． （1）解不等式 ( ) 4fx ； （2）若关于 x 的不等式 2( ) 5| 1| 5f x x a a+ +  − + 的解集不是空集，求 a 的取值范围．