2018版高考数学（人教A版理）一轮复习：第2章 第13节 课时分层训练16 5页

课时分层训练(十六)　‎ 定积分与微积分基本定理 A组　基础达标 ‎(建议用时：30分钟)‎ 一、选择题 ‎1．定积分(2x＋ex)dx的值为(　　)‎ A．e＋2　　　　　　 B.e＋1‎ C．e D.e－1‎ C　[(2x＋ex)dx＝(x2＋ex)|＝1＋e1－1＝e.故选C.]‎ ‎2．直线y＝4x与曲线y＝x3在第一象限内围成的封闭图形的面积为(　　) ‎ ‎【导学号：01772095】‎ A．2 B.4 C．2 D.4‎ D　[令4x＝x3，‎ 解得x＝0或x＝±2，‎ ‎∴S＝(4x－x3)dx＝＝8－4＝4，故选D.]　‎ ‎3．从空中自由下落的一物体，在第一秒末恰经过电视塔顶，在第二秒末物体落地，已知自由落体的运动速度为v＝gt(g为常数)，则电视塔高为(　　)‎ A.g B.g C.g D.2g C　[由题意知电视塔高为 gtdt＝gt2|＝2g－g＝g.]　‎ ‎4．已知f(x)为偶函数且f(x)dx＝8，则－6f(x)dx等于(　　) ‎ ‎【导学号：01772096】‎ A．0　　　 B.4‎ C.8　　　 D.16‎ D　[原式＝－6f(x)dx＋f(x)dx，‎ 因为原函数为偶函数，即在y轴两侧的图象对称．所以对应的面积相等，‎ 即－6f(x)dx＝2f(x)dx＝8×2＝16.]　‎ ‎5．若dx＝3＋ln 2(a>1)，则a的值是(　　)‎ A．2　　　 B.3‎ C.4　　　 D.6‎ A　[由题意知dx＝(x2＋ln x)|＝a2＋ln a－1＝3＋ln 2，解得a＝2.]‎ 二、填空题 ‎6．(2017·陕西质检(二))(x＋cos x)dx＝________.‎ 　[(x＋cos x)dx＝|＝.]‎ ‎7．设变力F(x)作用在质点M上，使M沿x轴正向从x＝1运动到x＝10(单位：m)，已知F(x)＝x2＋1(单位：N)且和x轴正向相同，则变力F(x)对质点M所做的功为________J. 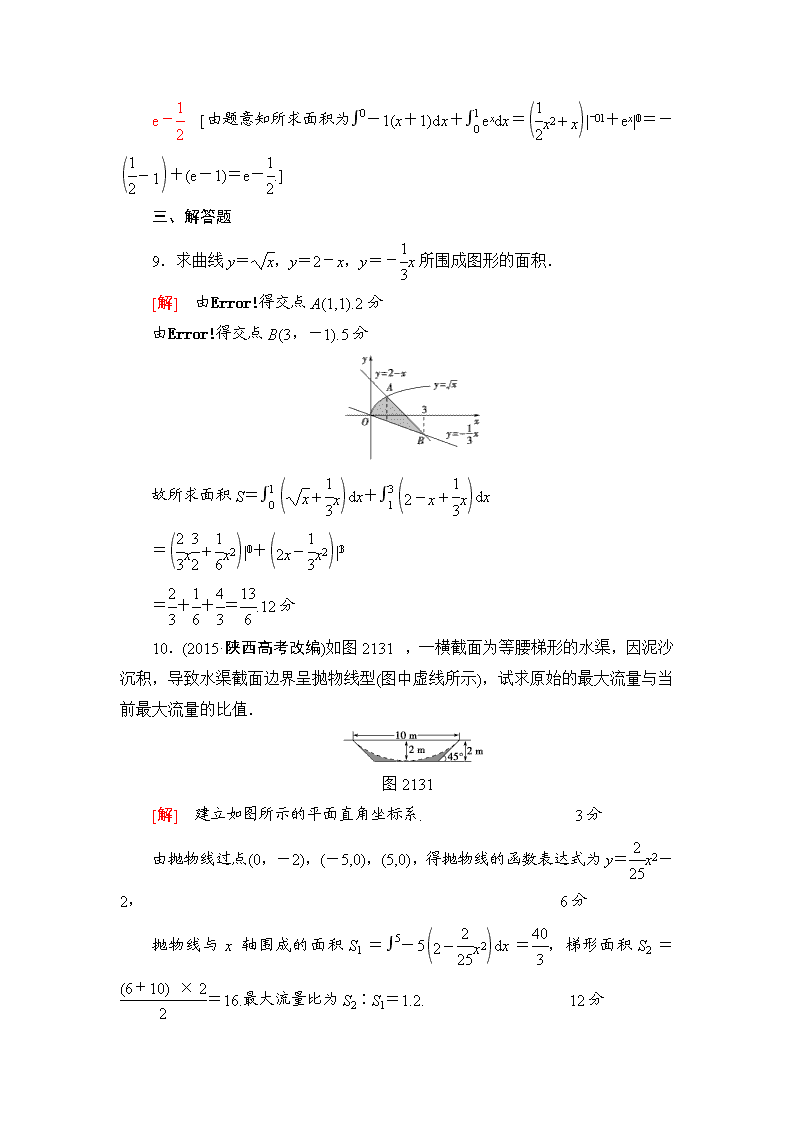‎ ‎【导学号：01772097】‎ ‎342　[变力F(x)＝x2＋1使质点M沿x轴正向从x＝1运动到x＝10所做的功为 W＝∫F(x)dx＝∫(x2＋1)dx ‎＝|＝342(J)．]‎ ‎8．(2017·洛阳统考)函数f(x)＝的图象与直线x＝1及x轴所围成的封闭图形的面积为________．‎ e－　[由题意知所求面积为－1(x＋1)dx＋exdx＝|＋ex|＝－＋(e－1)＝e－.]‎ 三、解答题 ‎9．求曲线y＝，y＝2－x，y＝－x所围成图形的面积．‎ ‎[解]　由得交点A(1,1).2分 由得交点B(3，－1).5分 故所求面积S＝dx＋dx ‎＝|＋| ‎＝＋＋＝.12分 ‎10．(2015·陕西高考改编)如图2131，一横截面为等腰梯形的水渠，因泥沙沉积，导致水渠截面边界呈抛物线型(图中虚线所示)，试求原始的最大流量与当前最大流量的比值．‎ 图2131‎ ‎[解]　建立如图所示的平面直角坐标系. 3分 由抛物线过点(0，－2)，(－5,0)，(5,0)，得抛物线的函数表达式为y＝x2－2， 6分 抛物线与x轴围成的面积S1＝－5dx＝，梯形面积S2＝＝16.最大流量比为S2∶S1＝1.2. 12分 B组　能力提升 ‎(建议用时：15分钟)‎ ‎1．若f(x)＝x2＋2f(x)dx，则f(x)dx＝(　　)‎ ‎【导学号：01772098】‎ A．－1 B.－ C. D.1‎ B　[由题意知f(x)＝x2＋2f(x)dx，‎ 设m＝f(x)dx，∴f(x)＝x2＋2m，‎ f(x)dx＝(x2＋2m)dx＝| ‎＝＋2m＝m，∴m＝－.]‎ ‎2．曲线＋＝1与两坐标轴所围成图形的面积是________．‎ 　[将曲线＋＝1转化为y＝(1－)2，且x≥0，y≥0.令y＝0，可知曲线与x轴交点为(1,0)，则曲线与两坐标轴所围成的面积S＝(1－)2dx＝(1－2＋x)dx＝|＝1－＋＝.]‎ ‎3．已知函数f(x)＝x3－x2＋x＋1，求其在点(1,2)处的切线与函数g(x)＝x2围成的图形的面积．‎ ‎[解]　∵(1,2)为曲线f(x)＝x3－x2＋x＋1上的点，‎ 设过点(1,2)处的切线的斜率为k，‎ 则k＝f′(1)＝(3x2－2x＋1)|x＝1＝2，‎ ‎∴过点(1,2)处的切线方程为y－2＝2(x－1)，‎ 即y＝2x.y＝2x与函数g(x)＝x2围成的图形如图.5分 由可得交点A(2,4)，7分 ‎∴y＝2x与函数g(x)＝x2围成的图形的面积 S＝(2x－x2)dx＝|＝4－＝.12分