专题2-6 函数性质综合运用（测）-2018年高考数学一轮复习讲练测（江苏版） 9页

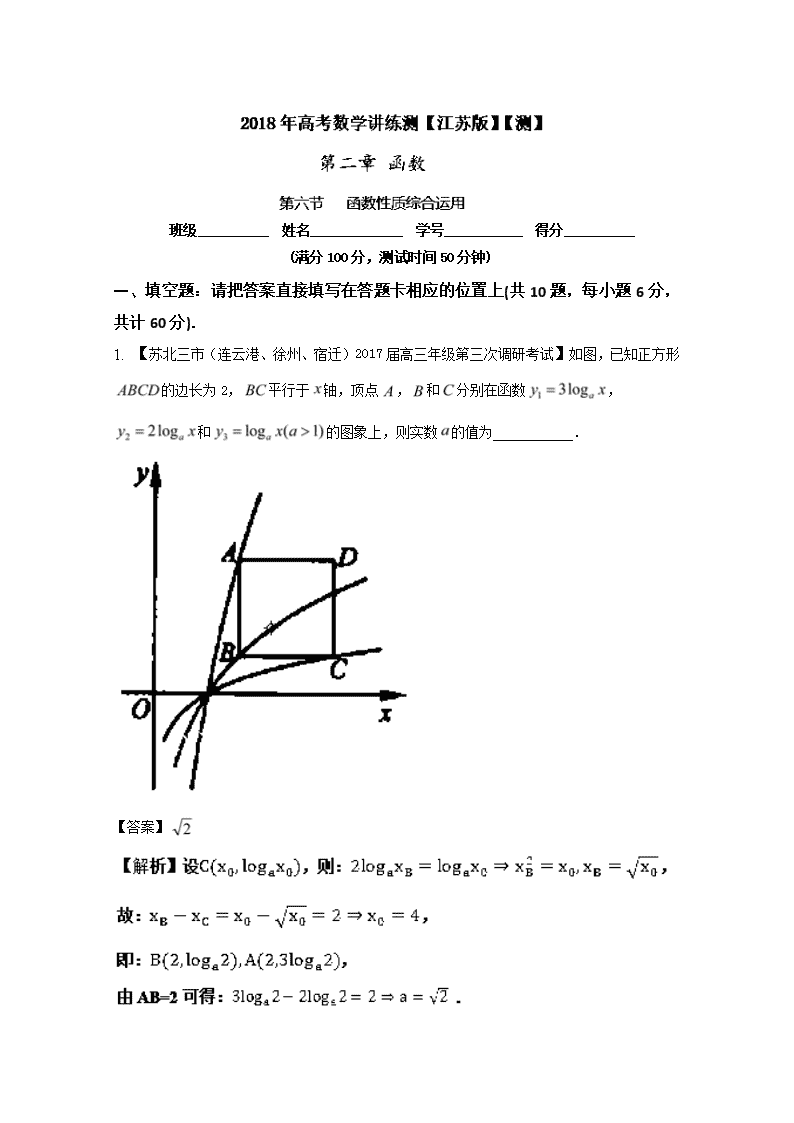
班级__________ 姓名_____________ 学号___________ 得分__________‎ ‎(满分100分，测试时间50分钟)‎ 一、填空题：请把答案直接填写在答题卡相应的位置上(共10题，每小题6分，共计60分)．‎ ‎1. 【苏北三市（连云港、徐州、宿迁）2017届高三年级第三次调研考试】如图，已知正方形的边长为2，平行于轴，顶点，和分别在函数，和的图象上，则实数的值为__________．‎ ‎【答案】‎ ‎2. 【2016-2017学年度苏锡常镇四市高三教学情况调研（二）】已知函数若函数有三个零点，则实数的取值范围为 ．‎ ‎【答案】 ‎3. 【南京市、盐城市2017届高三年级第一次模拟】在平面直角坐标系中，已知点为函数的图象与圆的公共点，且它们在点处有公切线，若二次函数的图象经过点，则的最大值为 ▲ .‎ ‎【答案】‎ ‎【解析】设，则由得，而二次函数正好过三点，所以 ‎4. 【镇江市2017届高三年级第一次模拟】已知函数与函数的图象共有（）个公共点：， ，… ，，则 ．‎ ‎【答案】2‎ ‎【解析】函数与函数的图象都关于对称，共有2个公共点：所以 ‎ ‎5. 【2017年第三次全国大联考江苏卷】已知，若在上恒有，则实数的取值范围是_____________．‎ ‎【答案】 ‎6.已知幂函数f(x)=x2+m是定义在区间[-1,m]上的奇函数,则f(m+1)=__________.‎ ‎【答案】8.‎ ‎【解析】因为幂函数在[-1,m]上是奇函数,‎ 所以m=1,所以f(x)=x2+m=x3,‎ 所以f(m+1)=f(1+1)=f(2)=23=8.‎ ‎7.已知函数f(x)=x2+,g(x)=‎1‎‎2‎x-m.若∀x1∈ [1,2],∃x2∈[-1,1]使f(x1)≥g(x2),则实数m的取值范围是 ‎__________.‎ ‎【答案】‎‎-‎5‎‎2‎,+∞‎ ‎【解析】要使∀x1∈[1,2],∃x2∈[-1,1],‎ ‎8. f(x)是定义在R上的偶函数,当x<0时,有f(x)+xf′(x)<0,且f(-4)=0,则不等式xf(x)>0的解集为________.‎ ‎【答案】(-∞,-4)∪(0,4)‎ ‎【解析】因为[xf(x)]′=f(x)+xf′(x),根据已知条件可知,x<0时,‎ ‎[xf(x)]′<0,所以F(x)=xf(x)在(-∞,0)上递减,又因为f(x)是R上的偶函数,所以F(x)是R上的奇函数,则F(x)在(0,+∞)上递减,因为f(-4)=0,f(x)为R上的偶函数,所以f(4)=0,则F(-4)=F(4)=0,‎ 综合图象可知xf(x)>0的解集应为(-∞,-4)∪(0,4).‎ ‎9已知符号函数sgn(x)=‎1,x>0,‎‎0,x=0,‎‎-1,x<0,‎则函数f(x)=sgn(lnx)-lnx的零点个数为________.‎ ‎【答案】3‎ ‎【解析】依题意得f(x)=sgn(lnx)-lnx=‎1-lnx,x>1,‎‎0,x=1,‎‎-1-lnx,0f′(x),则f(2014)与e‎2014f(0)大小关系为________.‎ ‎【答案】f(2014)f′(x),并且ex>0,‎ 所以g′(x)<0,故函数g(x)=f(x)‎ex在R上单调递减,‎ 所以g(2014)g(x2)恒成立,求实数a的取值范围.‎ ‎【答案】(1) f(x)min=a‎2‎‎+4a-3,a≤1,‎‎1+a‎2‎,a>1.‎ (2) (-∞,-5)∪(1,+∞).‎ ‎【解析】(1)函数f(x)的对称轴是x=a,‎ 当a≤1时,f(x)min=f(2)=a2+‎4a-3,‎ 当a>1时,f(x)min=f(0)=1+a2,‎ 所以f(x)min=‎a‎2‎‎+4a-3,a≤1,‎‎1+a‎2‎,a>1.‎ ‎(2)令‎2-x=t(t∈[0,‎2‎]),则x=2-t2,‎ 所以g (x)=h(t)=-t2+t+,‎ 因为对称轴t=∈‎0,‎‎2‎,所以g(x)max=h(t)max=2,‎ 由题意,要使对于∀x1,x2∈[0,2],f(x1)>g(x2)恒成立,只要f(x)min>g(x)max即可,‎ 所以当a≤1时,f(x)min=a2+‎4a-3>2,‎ 解得：a<-5,‎ 当a>1时,f(x)min=1+a2>2,解得：a>1,‎ 综上所述,a∈(-∞,-5)∪(1,+∞).‎ ‎13.设a∈[-2,0],已知函数f(x)=‎x‎3‎‎-(a+5)x,x≤0,‎x‎3‎‎-a+3‎‎2‎x‎2‎+ax,x>0.‎ ‎(1)证明f(x)在区间(-1,1)内单调递减,在区间(1,+∞)内单调递增.‎ ‎(2)设曲线y=f(x)在点Pi(xi,f(xi))(i=1,2,3)处的切线相互平行,且x1x2x3≠0,证明x1+x2+x3>-‎1‎‎3‎.‎ ‎【答案】(1)详见解析， (2) 详见解析. ‎ 由3x‎1‎‎2‎-(a+5)=g(x2)-‎2a+5‎‎3‎+a+3‎‎3‎,设t=‎2a+5‎‎3‎,则a=‎3t‎2‎-5‎‎2‎,因为a∈‎-2,0‎,所以t∈‎3‎‎3‎‎,‎‎15‎‎3‎,故x1+x2+x3>-t+‎3t‎2‎+1‎‎6‎=‎1‎‎2‎(t-1)2-‎1‎‎3‎≥-‎1‎‎3‎,即x1+x2+x3>-‎1‎‎3‎. ‎ ‎14. 【2016高考上海理数】已知，函数.‎ ‎（1）当时，解不等式；‎ ‎（2）若关于的方程的解集中恰好有一个元素，求的取值范围；‎ ‎（3）设，若对任意，函数在区间上的最大值与最小值的差不超过1，求的取值范围.‎ ‎【答案】（1）．（2）．（3）．‎ ‎（3）当时，，，‎