- 834.00 KB
- 2021-04-12 发布
2018届高三学年10月份月考 数学文科试题
一、选择题(每题5分,满分60分)
1.已知集合,,那么
A. B. C. D.
2.已知是虚数单位,复数,则的虚部为( )
A. B. C. D.
3. 下列关于命题的说法错误的是( )
A. 命题“若 ,则”的逆否命题为“若,则”
B. “”是“函数在区间上为增函数”的充分不必要条件
C. 命题“,使得”的否定是:“均有”
D. “若为的极值点,则”的逆命题为真命题
4. 若点在直线上,则的值等于( )
A. B. C. D.
5. 已知等差数列1, , ,等比数列4, , ,则该等比数列的公比为( )
A. B. C. 或 D. 10或
6. 设,满足约束条件,若目标函数的最大值为,
则的最大值为( )
A.1 B.2 C.3 D.4
7. 已知单位向量与的夹角为,向量与的夹角为,则( )
A. B. C. 或 D.
8.已知曲线, ,则下列说法正确的是( )
A. 把上各点横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线
B. 把上各点横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线
C. 把曲线向右平移个单位长度,再把得到的曲线上各点横坐标缩短到原来的,纵坐标不变,得到曲线
D. 把曲线向右平移个单位长度,再把得到的曲线上各点横坐标缩短到原来的,纵坐标不变,得到曲线
9. 函数(其中为自然对数的底数)的图象大致为
A. B. C. D.
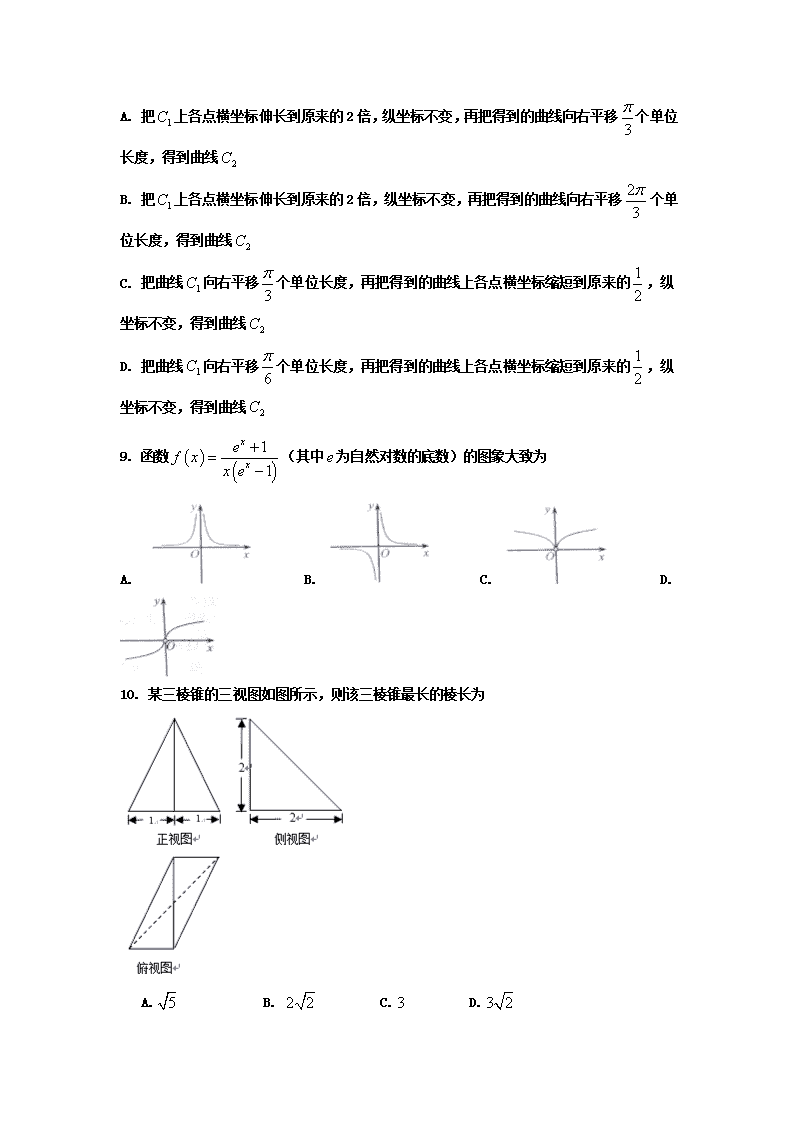
10. 某三棱锥的三视图如图所示,则该三棱锥最长的棱长为
A. B. C. D.
11.已知数列满足, 是等差数列,则数列的前10项的和( )
A. 220 B. 110 C. 99 D. 55
12. 已知定义在上的函数满足:函数的图象关于直线对称,且当是函数的导函数)成立.若, ,则的大小关系是( )
A. B. C. D.
二、填空题(每题5分,共20分)
13. 已知向量=(1,–1),=(6,–4).若⊥(t),则实数t的值为________.
14. 已知等腰直角三角形的直角边长为3,将该三角形绕其斜边所在直线旋转一周而形成的曲面所围成的几何体的体积为
15. 已知的三边长分别为3,5,7,则该三角形的外接圆半径等于_________
16. 已知函数,函数,若存在,对任意都有成立,则实数的取值范围是
三、解答题(17题—21题,每题12分,选做题10分)
17. 已知函数在一个周期内的部分对应值如下表:
(Ⅰ)求的解析式;
(Ⅱ)求函数的最大值和最小值.
18. 在△ABC中,角A,B,C的对边分别为a,b,c,且a=2b,又sinA,sinC,sin
B成等差数列.
(1)求cosA的值;
(2)若,求c的值.
19. 已知数列是首项为正数的等差数列,数列的前项和为.
(I)求数列的通项公式;
(II)设,求数列的前项和.
20. 设椭圆E的方程为点O为坐标原点,点A的坐标为,点B的坐标为(0,b),
点M在线段AB上,满足直线OM的斜率为.
(Ⅰ)求E的离心率e;
(Ⅱ)设点C的坐标为(0,-b),N为线段AC的中点,证明:MNAB.
21. 已知函数
(I)求的单调区间;
(II)设曲线与轴正半轴的交点为P,曲线在点P处的切线方程为,
求证:对于任意的正实数,都有;
(III)若方程有两个正实数根且,求证:.
四、选考题
22. 选修4一4:坐标系与参数方程
已知极坐标系的极点在平面直角坐标系的原点处,极轴与轴的正半轴重合,且长度单位相同;曲线的方程是,直线的参数方程为(为参数,),设,直线与曲线交于两点.
(1)当时,求的长度;
(2)求的取值范围.
23. 选修4一5:不等式选讲
已知函数,.
(1)解关于的不等式();
(2)若函数的图象恒在函数图象的上方,求的取值范围.
文科数学答案
一、选择ACDBC/DBBAC/BA
二、填空13、—5 14、 15、 16、
三、解答题
17.解:(Ⅰ)由表格可知,的周期,
所以.
又由,且,所以.
所以. …………………6分
(Ⅱ)
.
由,所以当时,有最大值;
当时,有最小值.
18. (Ⅰ)∵sinA,sinC,sinB成等差数列,
∴sinA+sinB=2sinC
由正弦定理得a+b=2c
又a=2b,可得,
∴;
(2)由(1)可知,
得,
∴,
∵,
∴
,
解得:
故得时,c的值为4.
19. (I)设数列的公差为,
令得,所以.
令得,所以.
解得,所以
(II)由(I)知所以
所以
两式相减,得
所以
20. (Ⅰ)解:由题设条件知,点,又从而.
进而,故.
(Ⅱ)证:由是的中点知,点的坐标为,可得.
又,从而有
由(Ⅰ)得计算结果可知所以,故.
21. (I)由,可得,当 ,即 时,函数 单调递增;当 ,即 时,函数 单调递减.所以函数 的单调递增区间是 ,单调递减区间是.
(II)设 ,则 , 曲线 在点P处的切线方程为 ,即,令 即 则.
由于在 单调递减,故在单调递减,又因为,所以当时,,所以当时,,所以 在单调递增,在单调递减,所以对任意的实数x, ,对于任意的正实数,都有.
(III)由(II)知 ,设方程 的根为 ,可得,因为在 单调递减,又由(II)知 ,所以 .类似的,设曲线 在原点处的切线为 可得 ,对任意的,有 即 .设方程 的根为 ,可得 ,因为 在 单调递增,且 ,因此, 所以 .
22. (1)曲线的方程为
当时,直线,
(2)设为相应参数值,,,
,
23. (1)不等式即为,
当时,解集为,即;
当时,解集为全体实数;
当时,解集为
(2)的图象恒在函数图象的上方,即为对任意实数恒成立,
即恒成立,
又对任意实数恒有,
于是得,即的取值范围是