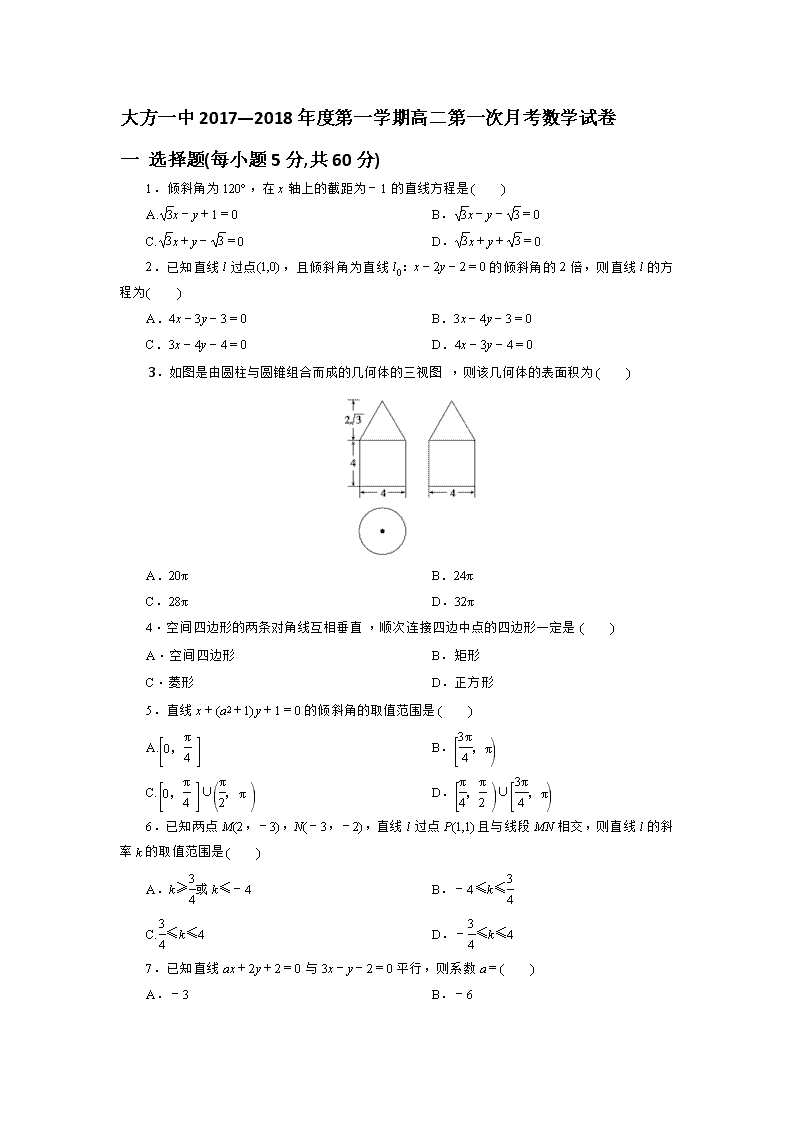- 106.00 KB
- 2021-04-12 发布
大方一中2017—2018年度第一学期高二第一次月考数学试卷
一 选择题(每小题5分,共60分)
1.倾斜角为120°,在x轴上的截距为-1的直线方程是( )
A.x-y+1=0 B.x-y-=0
C.x+y-=0 D.x+y+=0
2.已知直线l过点(1,0),且倾斜角为直线l0:x-2y-2=0的倾斜角的2倍,则直线l的方程为( )
A.4x-3y-3=0 B.3x-4y-3=0
C.3x-4y-4=0 D.4x-3y-4=0
3.如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为( )【来源:全,品…中&高*考+网】
A.20π B.24π
C.28π D.32π
4.空间四边形的两条对角线互相垂直,顺次连接四边中点的四边形一定是( )
A.空间四边形 B.矩形
C.菱形 D.正方形
5.直线x+(a2+1)y+1=0的倾斜角的取值范围是( )
A. B.
C.∪ D.∪
6.已知两点M(2,-3),N(-3,-2),直线l过点P(1,1)且与线段MN相交,则直线l的斜率k的取值范围是( )
A.k≥或k≤-4 B.-4≤k≤
C.≤k≤4 D.-≤k≤4
7.已知直线ax+2y+2=0与3x-y-2=0平行,则系数a=( )
A.-3 B.-6
C.- D.
8.已知直线l1:y=2x+3,直线l2与l1关于直线y=-x对称,则直线l2的斜率为( )
A. B.-
C.2 D.-2
9.执行如图所示的程序框图,若输入的a值为1,则输出的k值为( )
A.1 B.2
C.3 D.4
10.平行于直线2x+y+1=0且与圆x2+y2=5相切的直线的方程是( )
A.2x+y+5=0或2x+y-5=0
B.2x+y+=0或2x+y-=0
C.2x-y+5=0或2x-y-5=0
D.2x-y+=0或2x-y-=0
10.已知圆C的圆心是直线x-y+1=0与x轴的交点,且圆C与直线x+y+3=0相切,则圆C的方程是( )
A.(x+1)2+y2=2 B.(x+1)2+y2=8
C.(x-1)2+y2=2 D.(x-1)2+y2=8
11.在平面直角坐标系内,若曲线C:x2+y2+2ax-4ay+5a2-4=0上所有的点均在第四象限内,则实数a的取值范围为( )
A.(-∞,-2) B.(-∞,-1)
C.(1,+∞) D.(2,+∞)
12.设点M (x0,1),若在圆O∶x2+y2=1上存在点N,使得∠OMN=45°,则x0的取值范围是( )
A.[-1,1] B.[-,]
C.[-,] D.[-,]
二 填空题(每小题5分,共20分)
13.直线3x-4y+k=0在两坐标轴上的截距之和为2,则实数k=________.
14.过两直线2x-y-5=0和x+y+2=0的交点且与直线3x+y-1=0平行的直线方程为________.
15.已知两点A(-2,0),B(0,2),点C是圆x2+y2-2x=0上任意一点,则△ABC面积的最小值是________.
16.经过P(-2,4)、Q(3,-1)两点,并且在x轴上截得的弦长等于6的圆的方程________.
三 解答题
17(10分).一条直线经过点A(-2,2),并且与两坐标轴围成的三角形的面积为1,求此直线的方程.
18(12分).设直线l的方程为x+my-2m+6=0,根据下列条件分别确定m的值:
(1)直线l的斜率为1;
(2)直线l在x轴上的截距为-3.
19(12分).某篮球队6名主力队员在最近三场比赛中投进的三分球个数如表格所示:
队员i
1
2
3
4
5
6
三分球个数
a1
a2
a3
a4
a5
a6
统计该6名队员在最近三场比赛中投进的三分球总数的程序框图如图所示.
(1)试在判断框内填上条件;
(2)求输出的s的值.
20(12分).已知直线l1:2x+3y+8=0,l2:x-y-1=0,l3:x+ky+k+=0,分别求满足下列条件的k的值:
(1)l1,l2,l3相交于一点;
(2)l1,l2,l3围成三角形.
21(12分).已知直线l:y=kx+1,圆C:(x-1)2+(y+1)2=12.
(1)试证明:不论k为何实数,直线l和圆C总有两个交点;
(2)求直线l被圆C截得的最短弦长.
22(12分).如图所示,四边形ABCD中,AB⊥AD,AD∥BC,AD=6,BC=4,AB=2,点E,F分别在BC,AD上,且E为BC的中点,EF∥AB.现将四边形ABEF沿EF
折起,使二面角AEFD等于60°.
(1)设P为AD的中点,求证:CP∥平面ABEF;
(2)求二面角A—CD—F的正切值.